Построение многомерных дискретных распределении с заданной корреляционной структурой

Пусть заданы нормальные распределения со сред-

ними значениями μ₁, …, μ _d и стандартными отклонениями σ₁, …, σ _d . Для произвольной корреляционной матрицы R существует единственное многомерное нормальное распределение, обладающее такими маргинальными распределениями и корреляционной матрицей. Хорошо известный алгоритм воспроизведения соответствующего случайного вектора X = ( X 1 , … , X d ) основан на факторизации ковариационной матрицы.

Обозначим

(^G 1

л =

^П 2

0 )

( 0   0

n d)

диагональную матрицу со стандартными отклонениями на диагонали, тогда C = Λ R Λ является ковариационной матрицей распределения вектора X . Будучи неотрицательно определенной и симметричной, ковариационная матрица C может быть представлена в виде

C = A′A (1)

с некоторой матрицей A , причем последняя определяется не одним образом. Примерами такого представления являются разложение Холецкого и ортогональное разложение.

При наличии разложения (1) вектор X воспроизводится из стандартного нормального случайного вектора Z по формуле

X = A′Z. (2)

Действительно, для Z справедливо E ZZ′ = I , где I – единичная матрица соответствующего размера, поэтому E XX′ = E ( A′ZZ′A ) = A′ ( E ZZ′ ) A = A′A = C , так

что X обладает требуемой ковариационной структурой.

В случае, когда компоненты X имеют фиксированные дискретные распределения, аналогичный метод оказывается неприменимым. Во-первых, заданным маргинальным распределениям и ковариационной матрице соответствуют, вообще говоря, многие многомерные дискретные распределения. Может оказаться и так, что подходящее многомерное распределение не существует.

Во-вторых, алгоритм вращения (2) не сохраняет дискретную решетку значений, на которой задано распределение.

В работах [1; 2] анонсированы методы воспроизведения двумерного дискретного распределения с заданными маргинальными распределениями и корреляцией, основанные на смесях некоторых базовых распределений и минимизации уклонения от независимого распределения. В настоящей работе предлагается обоснование этих методов.

Описание двумерного дискретного распределения. Пусть размерность d = 2 . Обозначим K = {1,…, m } × {1,…, n } . Дискретное распределение вектора X = ( X ₁ , X ₂) ′ задается на прямоугольной сетке значений { x 11 ,…, x 1 m } × { x 21 ,…, x 2 n } в виде P ( X 1 = x 1 i ; X 2 = x 2 j ) = r ij , ( i , j ) e K . Обозначим совместное распределение компонент вектора X :

r = { r j , ( i , j ) e K }.                     (3)

Здесь P(X1 = x1i) = pi, i = 1,…,m и P(X2 = x2j) = qj, j = 1,…,n, так что векторы p = (p1,…,pm), q = (q1,…,qn)           (4)

описывают маргинальные распределения компонент.

Средние значения

a 1 = ^EX 1 = Е ^Х 1 / Л , a 2 = EX 2 = lx 2j q j , i = 1                                      j = 1

a ,, = E ( XX , ) = E E^ x- _1Л , i = 1 j = 1

стандартные отклонения a = VE(X1 - EX1)2 , ^2 = VE(X2 - EX,)2

u v 2/5 - u - v

1/3 - u 1/2 - v u + v - 7/30

Область допустимых значений параметров задается неравенствами

0 < u <  1/3,0 <  v <  1/2,7/30 < u + v < 2/5   (13)

и представлена на рисунке. Окружностями на нем от-

мечены антикомонотонное R^– ( p , q )

и коэффициент корреляции

E ( X 1 X ₂) - EX 1 EX ₂ ^a 1 ^a 2

Г 0   7/30 1/6 )

R ( p , q ) =                        ;

(1/3 4/15   0 J независимое R0(p, q)

вычисляются как обычно.

Если маргинальные распределения (4) известны, то выполняются следующие соотношения:

₀        Г 2/15 1/5 1/15 )

R ⁰( p , q ) =                          ;

( 1/5  3/10 1/10 J

комонотонное R⁺ ( p , q ) распределение

m

E r ⁼ q j , j = ¹, - , ⁿ ;               ⁽⁶⁾

i = 1

n

E r j = Pi , i = 1, - , m .                ⁽⁷⁾

j = 1

1/3  1/15   0

R - ( p , q ) =                         .           (16)

( 0   13/30 1/6 J

Отметим, что среди m + n уравнений (6), (7) имеется лишь m + n – 1 независимых, поскольку сумма компонент любого распределения равна 1.

Если же дополнительно известен коэффициент корреляции c компонент X , то справедливо и уравнение

mn

EE ^x 1i ^x 2j r j = c ^a 1 ^a 2 + a 1 a 2 .          ⁽⁸⁾

i = 1 j = 1

Обозначим F ( p , q ) класс всех двумерных распределений (3) с маргинальными распределениями (4) (его еще называют классом Фреше), а F_c ( p , q ) его подкласс распределений с корреляцией c . Известно [3], что среди всех распределений в F ( p , q ) наименьшей корреляцией c min = c min ( p , q ) обладает антикомонотон-ное распределение R^– ( p , q ), а наибольшей корреляцией c max = c max ( p , q ) обладает комонотонное распределение R⁺ ( p , q ), причем c min > –1 и c max <  1. Класс Фреше представим в виде

f ( p , q ) =    U F c ( p , q ).          ⁽⁹⁾

c ^G [ c min , c max ]

Обозначим еще R ⁰( p , q ) независимое распределение из класса Фреше F ( p , q ) .

Пример . Пусть на сетке значений

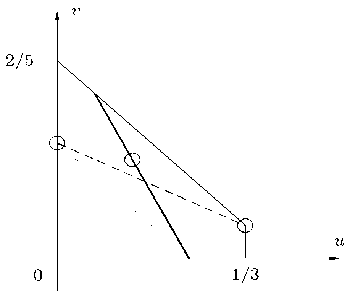
Допустимая область в плоскости параметров ( u , υ ): ––– – некоррелированные компоненты; О (слева направо) – антикомонотонное, независимое и комонотонное распределения; –––– – решения задачи 1

Класс F c ( p , q ) описывается в параметрическом представлении следующим уравнением:

v = — + c

- 2 u .

Некоррелированные распределения лежат на отрезке прямой, описываемом выражением

u + v = —,— <  u < — . 15 15

{0, 1, 2} × {0, 1}                 (10)

Коэффициент корреляции в данном примере за-

заданы маргинальные распределения

p = (1/3, 1/2, 1/6), q = (2/5, 3/5).       (11)

ключен в интервале c G

^—

Основные характеристики маргинальных

распре-

102;

делений равны:

a 1 = , a 2 = - , ^a 1

—, a, = —. 6 2 5

Двухпараметрическое представление класса Фреше имеет вид

Критерий близости к независимому распределению. Теперь сформулируем две задачи выбора из всего множества совместных распределений, удовлетворяющих условиям (6)–(8), единственного распределения, наименее уклоняющегося от независимого распределения в смысле критерия

1mn

f(r)=tEE(r-pq/) ^min.

2 i=i j =1

сле этих операций система уравнений запишется в виде

A Y = b ,                      (25)

Задача 1. В первой задаче целевая функция (19) минимизируется при ограничениях (6)–(8).

Функция Лагранжа этой задачи имеет вид

1 m n               2 n Л mA

L(r,x,ц,v)=-EE(rij-pa^ +EXjlEг-qj l+ 2 i=1 j=1                        j=1 V i=1

m    nmn

⁺Е ц . l E r u -р. l^+vl EE ^xn^x 2j r ij- c ° 1 ° 2 - a a 2 i = 1 V j = 1            у V i = 1 j = 1

Дифференцируя функцию Лагранжа по всем переменным и приравнивая производные к нулю, получаем уравнение aL / а гы = (rH - pq)+x i+ц k+v x 1 kx 21 = = 0, k = 1,- m, l = 1,- n,

а также выражения (6)–(8). Отметим, что ввиду соот-mn ношения E Pi =E qj = 1 в системе (6)—(8) одно из i =1          j =1

уравнений, например первое, является следствием остальных, и его можно отбросить вместе с соответствующим множителем Лагранжа X 1 . Для решения полученной системы уравнений выразим элементы матрицы r из уравнения (20) в виде функции множителей Лагранжа X , ц , v :

r_y = P , q_y - ( X j +^+v x_tix 2 j ) = 0,( i , j ) e K . (21)

Подставив полученное выражение в уравнения (6)–(8), имеем:

-mXj-'EЦ—vx2j^Exn = 0,j = 2,-n ;(22)

i=1

• -EXj-nц-vxUE*2j = 0,i = 1,-m ;(23)

j=1

mn

EE ^x 1 i ^x 2j ( Pqj ^- ( ^X j +Ц ^{+ v x} 1 i ^x 2 j ) ) = c ° 1 ° 2 ⁺ a 1 a 2 . i = 1 j = 1

m    mmn

Обозначив 51 = e x1i, 52=Ex 2j, s12=E x2Ex 2j, i =1                j =1                  i =1

преобразуем последнее уравнение к виду

• -51 IEXjx2j- s2EEЦiX1i - v512 = cЦ°2.(24)

j=1

Обозначим In единичную матрицу размера n×n, а Jmn – прямоугольную матрицу размера m × n, все элементы которой равны 1. Далее обозначим x2 = (x22,-,x2n)',x 1 = (x11,-,x 1 m)'. В системе уравнений (6)–(8), как уже отмечалось, первое уравнение является следствием остальных, поэтому его можно отбросить. Кроме того, в полученной системе m + n уравнений относительно m + n + 1 неизвестных одну из неизвестных можно выбрать произвольным образом. Мы будем полагать X1 = 0 , что соответствует отбрасыванию первого столбца в матрице системы. По- где неизвестные множители Лагранжа обозначены

Y = ( X 2 , — , X n , Ц 1 , — , ц n , v )',

а матрица системы А и вектор правых частей имеют вид

- mIn-1 -J n-1, m - 51 x 2 A = - J , m, n-1 - nIm - 5 2 x 1 ' V - 51 x 2 ' -52 x1 512 У b = (0,-,0,cc1c2).

Квадратная система линейных уравнений (25) имеет единственное решение (26), добавляя в которое значение λ1 = 0, из (21) вычисляем искомое распреде- ление.

Задача 2. Целевая функция (19) минимизируется при ограничениях (6)–(8) и ги> 0,(i, j) e K.                (27)

Аналитическое решение этой задачи в общем виде недоступно, однако численные методы позволяют эффективно решать ее. Приведем решения для рассмотренного примера.

Максимальному значению c = cmax = 8 / V102 соот- ветствует решение

Г 1/3  1/15    0

r =

V 0   13/30 1/6

которое, как нетрудно заметить, представляет собой комонотонное распределение (16).

Минимальному значению c = cmin = -7 / V102 со- ответствует решение

/ 0   7/30 1/6

r =

V 1/3 4/15   0

представляющее собой антикомонотонное распределение (14).

Результаты работы позволяют эффективно строить дискретные вероятностные модели с заданной корреляционной структурой. Предложенная методика без труда обобщается на многомерный случай d > 2.