Построение моделей однослойных углеродных нанотрубок и расчет координат атомов в них

Углеродные нанотрубки сочетают в себе свойства молекул и твердого тела и могут рассматриваться как промежуточное состояние вещества. Эта особенность привлекает к себе внимание исследователей, изучающих фундаментальные особенности поведения данного объекта в различных условиях. Углеродные нанотрубки проявляют ряд уникальных свойств. Например, нанотрубки, имеющие различный угол ориентации графитовой плоскости относительно оси трубки, имеют различные электронные характеристики, что может быть использовано при создании электронных устройств следующего поколения. Указанные особенности, представляющие значительный научный интерес, могут быть положены в основу эффективного прикладного использования нанотрубок в различных областях науки и технологии. Несмотря на огромное число теоретических и экспериментальных работ по изучению углеродных кластерных наносистем, до сих пор нет единого подхода, позволяющего объяснить структуру и свойства новых форм углерода. В связи с этим приобретает особую актуальность развитие методов нахождения координат атомов в данных нанообъектах, которые необходимы для анализа структуры и теоретического расчета физических свойств.

Цель данной работы – разработка алгоритма формирования координат атомов в однослойных углеродных трубках любых типов.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ МОДЕЛЕЙ ОДНОСЛОЙНЫХ НАНОТРУБОК

Модельно формирование однослойной углеродной нанотрубки можно рассмотреть как про © Данилов С. В., Фофанов А. Д., 2011

цесс сворачивания плоской графеновой сетки в круговой цилиндр. Основными характеристиками структуры получаемых таким образом нанотрубок являются их длина, диаметр и такой параметр, как хиральность. Хиральность характеризуется двумя целыми числами ( n , m ), которые указывают местонахождение того шестиугольника сетки, который в результате свертывания должен совпасть с шестиугольником, находящимся в принятом начале координат . Эти числа называют индексами хиральности. Индексы однозначно задают размер слоя и направление сворачивания [1].

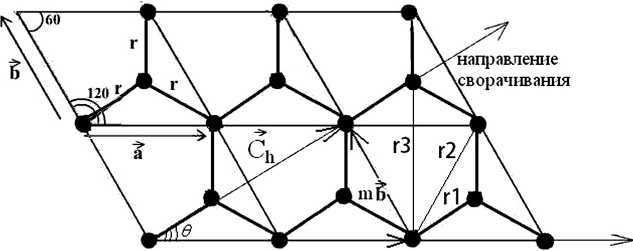
Согласно многим литературным источникам [3], [4], [5], [6], [7], [8], индексы хиральности задают трансляции вдоль осей x и y в кристаллографической гексагональной сетке с углом между векторами элементарных трансляций a и b , равным 60°. Однако это не совсем верно, так как с точки зрения классической кристаллографии данный угол равен 120° и, соответственно, ячейка выглядит несколько иным образом (рис. 1).

11?

Рис. 1. Гексагональная сетка, при сворачивании которой образуется нанотрубка (r1, r2, r3 – межатомные расстояния в графитовом кольце)

Для указания направления сворачивания вводится вектор хиральности C h = na + mb , где a и b – вектора элементарных трансляций вдоль двух направлений сетки, а n и m – количество трансляций вдоль соответствующих направлений, являющихся индексами хиральности. Также при этом следует иметь в виду, что в графите модули векторов элементарных трансляций ( a , b ) равны между собой и составляют величину 2,46 Å.

Направление, перпендикулярное вектору хиральности, – это ось формируемой нанотрубки. Таким образом, при сворачивании сетки вдоль данного вектора вокруг оси формируются «витки» нанотрубки. Модуль вектора хиральности определяет угол хиральности (угол сворачивания) нанотрубки (рис. 1):

cos( ^ ) = ² n - m =. (1) 2V n ² - nm + m ²

В зависимости от угла хиральности выделяют следующие типы нанотрубок:

• 1.    Для нанотрубок с индексом m = 0 угол хиральности равен 0^о. Такие трубки принято называть трубками типа «зиг-заг» (рис. 2а), которые описываются набором индексов ( n, 0 );

• 2.    В трубках с индексом n = 2m угол хиральности равен 30^о. Такие трубки, также называемые трубками типа «кресло» (рис. 2b), описываются набором индексов ( 2m, m );

• 3.    Указанные выше типы нанотрубок считаются идеальными, так как при сворачивании графенового слоя сохраняется идеальная структура (то есть не происходит искажения структуры гексагональной сетки). Данные идеальные трубки – предельные случаи. Все остальные нанотрубки – неидеальные, или хиральные, – имеют углы хиральности от 0 до 30^о [1], [2], [3], [4], [6], [7]. При формировании хиральной нанотрубки получается своего рода «спираль» в расположении атомов углерода (рис. 2с).

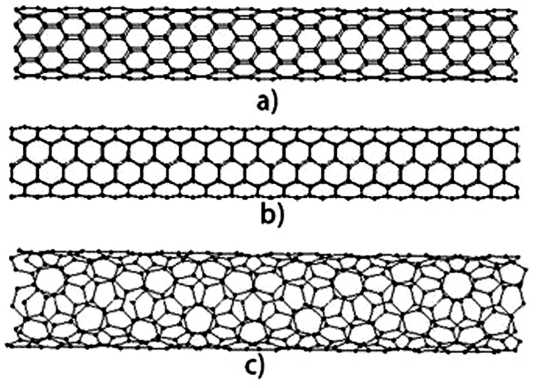
Рис. 2. Нанотрубки типа «зиг-заг» (n = 9, m = 0) (a), «кресло» (n = 10, m = 5) (b) и хиральные (n = 11, m = 3) (c)

В случае когда строится идеальн _u а _ur я нанотрубка, при «заворачивании» вектора C_h его конец совмещается с началом и образуется один замкнутый круговой виток. Таким образом, данный вектор соединяет два эквивалентных узла в сетке. Если же нанотрубка является хиральной, то формируется не один замкнутый виток, а «спираль». Но при этом начало и конец данной спирали (вне зависимости от количества полученных витков) – это также эквивалентные положения узлов сетки.

Модуль вектора хиральности определяет длину одного такого витка:

L = | C h | = a V( n ² — nm + m ²) . ⁽²⁾

Из известной формулы для длины окружности можно получить, что диаметр витка, равно как и диаметр получаемой нанотрубки, вычисляется как:

D = л] ( n ² - nm + m ²) ^r = ^ ( n ² - nm + m ²) a ■ ⁽³⁾ n n

Здесь r – межатомное расстояние в графите, равное 1,42 Å, a – параметр гексагональной ячейки, равный 2,46 Å [1], [5].

Для характеристики нанотрубки также вводится такой параметр, как степень хиральности [1], определяемый следующим образом:

K = ^m . (4) ch n

Так как индексы хиральности – целые числа, то в нанотрубках одинаковой степени хиральности соответствующие индексы кратны между собой. В этой связи можно ввести такой параметр, как «номер нанотрубки», который будет определяться как наибольший общий делитель (НОД) индексов хиральности:

d = НОД ( n, m ). (5)

Исходя из формулы (3) с учетом (5) можно сделать вывод, что для нанотрубок одинаковой степени хиральности (например, для трубок с индексами ( 2,1 ) и ( 6, 3 )) набор возможных диаметров дискретен, то есть нанотрубка не может иметь абсолютно произвольный диаметр, он определяется индексами хиральности.

Определенный таким образом параметр d – один из параметров симметрии, которые позволяют определить основные операции симметрии и принципы построения нанотрубок. Следующий параметр симметрии – d_R :

d_R = НОД (2 n - m, 2 m - n ) . (6)

Как и диаметр, длина нанотрубки также не может быть абсолютно произвольной. Это связано с тем, что в направлении, перпендикулярном направлению сворачивания трубки, то есть вдоль оси нанотрубки (или по ее длине), также имеется определенное количество ячеек графитовой сетки между двумя эквивалентными узлами, которое определяет «мотив», или уникальный, неповторимый характер расположения атомов вдоль оси нанотрубки. Так, вдоль оси нанотрубка состоит из целой последовательности таких «мотивов». Таким образом, длина также зависит от хиральности нанотрубки. Она определяется трансляционным вектором T = t1 a +12 b , перпендикулярным вектору хиральности (рис. 3), который характеризует минимальную длину (или шаг, трансляцию) вдоль направления оси нанотрубки.

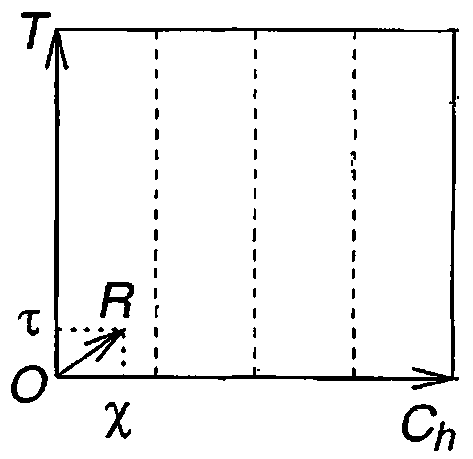
Рис. 3. Минимальная область «сетки», используемая для формирования нанотрубки

Данный вектор соединяет два эквивалентных положения узлов сетки вдоль оси получаемой нанотрубки. При этом коэффициенты t1 , t2 и длина вектора T определяются следующим об- разом:

_ 2 m n _ 2 n - m  —I _ 3 LL

-  d R  ’ ^{t 2}=" d ^{1 l=}T •

Таким образом, после того как определены вектор C _h , соответствующий минимальным индексам трубки с данной степенью хиральности, и вектор трансляции, в гексагональной сетке можно выделить прямоугольную область, ограниченную данными векторами, – так называемую трансляционную ячейку (рис. 3). При транс-лировани _u и _ur данной ячейки вдоль направления вектора C_h получается часть гексагональной сетки, при сворачивании которой можно сформировать нанотрубку бóльшего радиуса. Для вариации радиуса следует использовать различные индексы хиральности. При транслировании данной ячейки вдоль направления вектора T получается часть гексагональной сетки, при сворачивании которой можно сформировать нанотрубку бóльшей длины. Для вариации длины следует использовать различное целое число трансляционных векторов T .

Область, ограниченная векторами хираль- uur ности Ch и вектором, характеризующим длину нанотрубки, содержит N гексагональных колец, где N находится из следующего соотношения:

2( n ² - nm + m ²)

N = ----------<              (8)

dR

Для расчета остальных параметров симметрии (которые будут определять процедуру сворачивания) необходимо найти вектор симметрии R = pa + qb (рис. 3). Параметры p и q вычисляются из следующих соотношений:

d = nq - mp, 0 <  p <  n I d , 0 <  q <  m I d ,   (9)

где d рассчитывается по формуле (5).

Иногда вместо вектора симметрии в качестве аналога выделяют базовые операции симметрии R = ( ψ , τ ) (рис. 3), где

M         WL т = dT, W = 2п ,(или же ) z =   , (10)

NN          2n где τ – смещение вдоль оси трубки, ψ – угол поворота вокруг оси трубки, χ – смещение вдоль вектора хиральности, соответствующее углу поворота у, M - число оборотов на 360° вокруг оси трубки, находящееся из соотношения:

M = [ (2 n - m ) p + (2 m - n ) q ] I d_R .         (11)

В случае если строится нанотрубка типа «зигзаг», то есть индексы хиральности ( n, 0 ), параметры p = 1 , q = 1 , это приводит к значению M = 1 [4], [7].

МЕХАНИЗМ ФОРМИРОВАНИЯ КООРДИНАТ АТОМОВ В МОДЕЛЯХ ОДНОСЛОЙНЫХ УГЛЕРОДНЫХ НАНОТРУБОК

Рассмотрим процесс формирования координат атомов на примере нанотрубки с индексами хиральности n = 6 , m = 2 и одной трансляцией по длине трубки. Для этого вначале необходимо рассчитать параметры формируемой трубки по формулам (1–11) (табл. 1).

Таблица 1

Параметры нанотрубки с индексами хиральности n = 6 , m = 2

Параметр cos θ D, Å Kch d dR |T|, Å Значение 0,945 4,143 3 2 2 11,273 Параметр N P,q M τ ψ χ Значение 28 2,1 9 0,805 2,020 4,184 ur На рис. 4 вектор хиральности обозначен как C(6,2). Так как d = 2, то минимальная трубка той же степени хиральности – трубка с индексами хиральности n = 3, m = 1. Поэтому очевидно, что трубка (6,2) получается из трубки (3,1) трансли-рованиuеrм вдоль направления вектора хиральности C(3,1) . Можно сделать вывод, что узлы A и B – эквивалентные узлы.

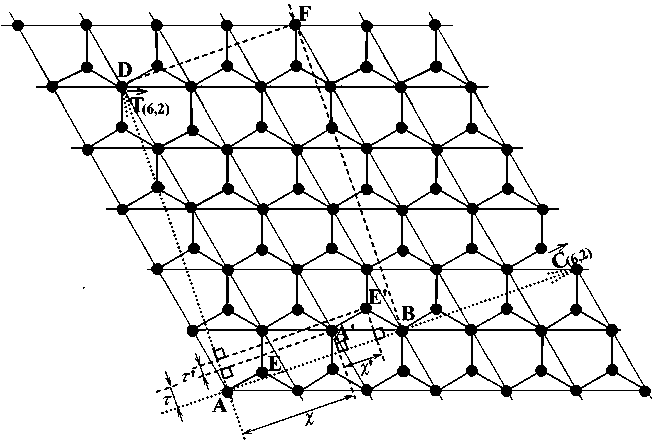
Рис. 4. Формирования координат атомов нанотрубки с индексами хиральности n = 6, m = 2

Вектор _ur транс _u л _r яции, обозначенный как T (6,2) (по сути, T (6,2) = T (3,1) ) (рис. 4), также соединяет 2 эквивалентных узла – A и D . Таким образом, минимальная область сетки, из которой может быть образована нанотрубка с данной степенью хиральности, ограничена узлами A , B , F , D – это все эквивалентные узлы сетки. Для нанотрубки (6,2) данная область транслируется вдоль направления вектора хиральности.

В начале построения в минимальной области сетки, из которой формируется нанотрубка, выделяется двухатомная ячейка, которая содержит атомы, находящиеся в двух кристаллографически неэквивалентных позициях в гексагональной ячейке. В данном случае это узлы A и E (рис. 4).

При «сворачивании» сетки на каждом шаге для каждого атома двухатомной ячейки применяются операции симметрии R = ( ψ , τ ). Таким образом, узел A «переходит» в узел A’ , E – в E’ (рис. 4). При этом следует отметить, что узел E дополнительно смещен относительно узла A (аналогично узел E’ относительно узла A’ ) как вдоль оси, так и вдоль вектора хиральности (рис. 4). Для нахождения этих дополнительных смещений следует воспользоваться следующими формулами:

^т = r sin(30 o - 0) , у ' = X I R ntr , (12)

где X = ^r cos⁽³⁰ o - ^{0 )} , 30 o — максимальный угол хиральности (соответствует нанотрубке типа «кресло»), θ – угол хиральности, R_Ntr – радиус формируемой нанотрубки.

Так как d ≠ 1, на каждом шаге необходимо рассчитывать координаты эквивалентных узлов, возникающих при транслировании вдоль вектора хиральности (например, на рис. 4 при расчете координат узла A нужно рассчитывать координаты узла B). Для этого необходимо знать дополнительные смещения вдоль оси и углы поворота вокруг оси трубки. Так, вдоль оси трубки узел, эквивалентный данному, располагается в том же положении, поэтому дополнительных смещений не будет. А вдоль вектора хиральности эквивалентный узел смещен относительно предыдуще- го эквивалентного узла (в нашем примере – узел B относительно узла A) (рис. 4). Данное смещение аналогично дополнительному повороту вокруг оси нанотрубки на угол:

Л 2 п

Nw =    .

d

После расчета параметров τ , ψ , χ , τ' , ψ' , χ' , Δψ производится последовательное движение вдоль оси нанотрубки и расчет на каждом шаге необходимых координат атомов (в декартовой системе): координата x – положение вдоль оси трубки, а координаты y и z получаются при вращении вокруг оси:

' У = R n,r *^sin Ф

<                                         ,

. z = R ntr *^cos Ф

где φ – текущий угол поворота вокруг оси нанотрубки.

Общее количество шагов при «расчете» нанотрубки вычисляется как:

L.   NT * T count = -r2^ = —---,               (15)

т т где LNtr – длина нанотрубки, NL – количество трансляций T по длине.

При моделировании нанотрубки следует обратить внимание на выбор индексов хиральности – n и m могут принимать ограниченное число значений. Так, индексы хиральности должны удовлетворять условиям:

n > 0, m > 0, n > 2 m .                 (16)

Также следует отметить, что если моделируются нанотрубки, индексы хиральности которых указаны с учетом распространенного в зарубежной литературе допущения, что угол между векторами элементарных трансляций в гексагональной ячейке равен 60о, то необходим пересчет указанных индексов хиральности в индексы, соответствующие классическому представлению (учитывающие, что угол равен 120о). Тогда следует воспользоваться следующими формулами перехода:

n ₂ = n 1 + m 1 , m ₂ = m 1 ,             (17)

где n₁ , m₁ – индексы хиральности для ячейки с углом 60^о, n₂ , m₂ – индексы хиральности для ячейки с углом 120^о.

NANOTUBE – ПРОГРАММА ГЕНЕРАЦИИ КООРДИНАТ АТОМОВ В МОДЕЛЯХ ОДНОСЛОЙНЫХ УГЛЕРОДНЫХ НАНОТРУБОК

На основе приведенных выше теоретических данных был разработан алгоритм формирования координат атомов в замкнутых однослойных углеродных нанотрубках любого типа. С использованием данного алгоритма на языке программирования Фортран была написана программа NanoTube .

При помощи полученной программы были смоделированы нанотрубки различного радиуса, длины, степени хиральности. При этом оказалось, что при малых значениях индексов хиральности радиус формируемой трубки получается настолько мал, что формируется некая структура, которую довольно трудно назвать нанотрубкой (рис. 5). Также следует отметить, что межатомные расстояния в таких структурах зачастую далеки от «нормальных» расстояний в графите (рис. 1, табл. 2).

Рис. 5. Фрагмент нанотрубки с индексами хиральности n = 2, m = 1 длиной 50 Å

При бóльших индексах хиральности происходит постепенное формирование структур, которые уже представляют замкнутые цилиндрические поверхности (рис. 2). При этом с увеличением радиуса нанотрубки межатомные расстояния выравниваются и приближаются к «графитовым» расстояниям (рис. 1, табл. 1).

Таблица 2

Сравнение межатомных расстояний в различных образцах

Расстояние (рис. 6)	Графит, R = ∞	Нанотрубка, n = 2, m = 1, R = 0,67813 Å	Нанотрубка, n = 40, m = 20, R = 13,5627 Å
r1	1,4203 Å	1,1746 Å 1,4046 Å	1,4196 Å 1,4202 Å
r2	2,4600 Å	1,8310 Å 2,4598 Å 2,4601 Å	2,4584 Å 2,4600 Å
r3	2,8406 Å	2,7260 Å	2,8354 Å 2,8402 Å

АНАЛИЗ РАЗЛИЧНЫХ ПРОГРАММ МОДЕЛИРОВАНИЯ ОДНОСЛОЙНЫХ НАНОТРУБОК

В процессе работы также был произведен поиск в сети Интернет аналогичных программ. В частности, были выделены 2 программы – MCAD [3] и TubeVbs [8]. Общая черта обеих программ – использование гексагональной ячейки с углом 60о. Рассмотрим особенности алгоритмов данных программ.

MCAD . Формирование координат атомов в нанотрубке происходит в несколько этапов:

• 1.    На основе параметров одной гексагональной ячейки формируются координаты всех узлов некоторой сетки максимально возможного размера;

• 2.    На основании введенных пользователем параметров моделируемой нанотрубки (длины и индексов хиральности) в данной сетке выделяется область, из которой будет сформирована нанотрубка;

• 3.    Для каждого узла сетки определяется, принадлежит ли он области, выделенной на втором шаге. Если принадлежит, то производится расчет декартовых координат на поверхности цилиндрически сформированной трубки;

• 4.    Результат выводится на экран с возможностью сохранения файла координат.

Особенности данной программы:

• 1.    Написана на языке JAVA, что дает возможность компилировать и запускать под различными операционными системами;

• 2.    Медленная работа по причине множества расчетов;

• 3.    Выделяется мало памяти, поэтому нельзя моделировать большие нанотрубки;

• 4.    Выходной файл – файл формата *.HIN (входной для программы HyperChem).

TubeVbs . Данный алгоритм схож с разработанным нами алгоритмом, так как основывался на тех же теоретических выкладках [5], [7]. Но в нем есть свои особенности:

• 1.    Вектора хиральности и трансляции откладываются от центра гексагонального кольца, то есть в «начальном» положении отсчета нет атома;

• 2.    Для моделирования трубки используются «винтовые» и «вращательные» операции симметрии:

• a)    «винтовой мотив» определяется как количество «двухатомных» ячеек, укладывающихся вдоль вектора хиральности;

• б)    «вращательный мотив» определяется как количество «винтовых мотивов» вдоль оси трубки;

• 3.    В программе учитывается возможность радиального искажения трубки: она может не являться идеальным цилиндром, у которого в основании – окружность.

Особенности данной программы:

• 1.    Программа написана на языке Visual Basic Script, что позволяет запускать ее только в среде Windows;

• 2.    Пользователь не может задать длину моделируемой трубки, лишь число трансляций вдоль оси, что не очень удобно;

• 3.    Высокая скорость работы, малые объемы требуемой памяти;

• 4.    Создается файл формата *.XYZ , содержащий лишь координаты атомов, что затрудняет использование данных файлов в других используемых нами программах.

Особенности разработанной программы NanoTube :

• 1.    Программа написана на языке программирования Фортран, что позволяет компилировать и запускать ее под разными операционными системами;

• 2.    Высокая скорость работы и малые объемы требуемой памяти;

• 3.    В процессе работы пользователю представляются именно физические параметры модели-

• руемой трубки, которые он может откорректировать;

• 4.    Выходной файл – файл формата *.DXR , который необходим для программ, реализующих расчет теоретических картин рассеяния рентгеновских лучей полученными объектами. Эти картины необходимы для интерпретации данных рентгенографических экспериментов по изучению структуры углеродных материалов [2].

Для сравнения программы NanoTube с другими программами ( MCAD , TubeVbs ) в каждой из них были смоделированы одинаковые нанотрубки (радиуса R_Ntr = 3,856 Å и длины L_Ntr = 41,964 Å ) и рассчитаны дифракционные картины рассеяния (в качестве критерия сравнения была взята интерференционная функция рассеяния, условно обозначенная как H(S)). Так, для программ MCAD и TubeVbs были приняты индексы хиральности n = 8 , m = 3 , а для программы NanoTube , исходя из формул перехода (17), соответствующие индексы хиральности равнялись n = 11 , m = 3 .

Результат сравнения представлен на рис. 6.

chiral H(S)

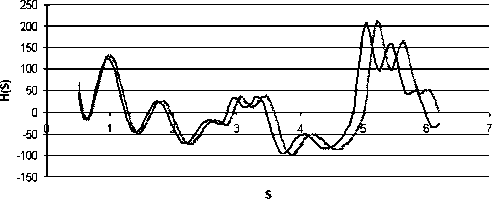
-----MCAD--TubeVbs-----NanoTube

Рис. 6. Зависимости H(S) для хиральных образцов, полученных разными программами

На приведенном графике видно, что зависимости H(S) , рассчитанные на основе координат атомов в нанотрубке, сгенерированных программой TubeVbs и нашей программой NanoTube , практически полностью совпадают. А H(S) , рассчитанная на основе координат, сгенерированных MCAD , всегда смещена, и чем больше модуль дифракционного вектора S , тем больше смещение.

С чем связано такое смещение, остается лишь догадываться, так как исходного кода к программе MCAD нет. В связи с этим возникают вполне обоснованные сомнения в корректности работы данной программы и ее использовании.

ВЫВОДЫ

Результатом данной работы является алгоритм, позволяющий получить координаты атомов в широком спектре однослойных углеродных цилиндрических нанотрубок различной длины, радиуса, степени хиральности. На основе генерируемых при помощи данной программы моделей нанотрубок возможен тщательный анализ получаемых таким образом структур с точки зрения особенностей внутреннего строения и их физических свойств. Кроме того, путем сопоставления теоретически рассчитанных дифракционных картин рассеяния, получаемых от сгенерированных моделей, и экспериментальных картин рассеяния рентгеновских лучей от реальных объектов возможна идентификация присутствия нанотрубок в исследуемых образцах.

Исследования проведены при поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы № П801 от 24 мая 2010 года.