Построение модели для оценки надежности телеметрической аппаратуры на основе маркированных графов

Выполнение расчетов вероятности безотказной работы телеметрической аппаратуры должно выполняться с учетом полученных данных по надежности и производительности для каждого структурного элемента системы.

Как показывает практика, осуществление подсчета характеристик структурных элементов в составе сложной технической системы, к которым относится телекоммуникационная аппаратура, является процессом не столь трудоемким, так как различных устройств и оборудования для реализации систем намного меньше, по сравнению непосредственно с самими, реализованными из данного оборудования. Также для получения характеристик системы возможно использование компьютерного моделирования, предоставляя иногда намного более точные результаты, так как использование компьютерных моделей позволит учесть максимально возможное количество событий. Для построения модели, а также описания происходящих в ней процессов наиболее удобным решением является использование маркированных графов. Это обусловлено некоторым сходством аппаратуры, построенной на основании блочной структуры. А так как в работе наиболее принципиален коэффициент готовности отдельного устройства, то его характеристики попросту не нужны для модели.

Основными условиями работоспособности системы в данном случае будут являться условия достижимости конечных узлов. Теория графов предоставляет большое количество путей для проверки данных условий, например, матрица достижимости, алгоритм поиска в глубину и т.д. [2].

Каждая вершина, представляющая собой узел на модели, может описывать как отдельное физическое устройство, так и целую субсеть, в состав которой входит набор физических элементов, объединение которых осуществляется на логическом уровне. Для данного узла в последнем случае характеристики надежности и производительности будут соответствовать суммарным характеристикам состава находящихся в нем структурных элементов.

Так как большинство элементов системы обладают несколькими портами для подключения других элементов, то могут быть попарно соединены несколькими каналами передачи данных. В данном случае в состав графа модели системы включаются кратные ребра, что делает его мультиграфом. В случае, если использование кратных ребер приводит к возникновению каких-либо трудностей, то в рамках задачи расчета коэффициента готовности всегда можно кратные ребра заменить одним ребром со схожими характеристиками в соответствии с рисунком 1. При этом оставшаяся пара ребер обладает неограниченной пропускной способностью и максимальным уровнем надежности. Исходя из данного факта далее можно рассматривать только вершины графа.

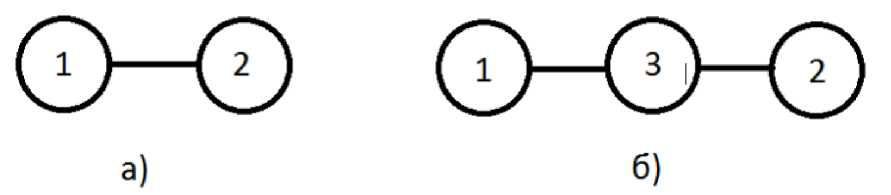
Рисунок 1 – Преобразование ребра {1, 2} в вершину 3

Структура полученной модели системы не может быть отнесена ни к последовательной, ни к параллельной, ни к древовидной. В связи с этим данные системы классифицируются как структурно-сложные системы.

Для осуществления расчётов параметров надежности структурносложных систем в шестидесятые годы двадцатого века были разработаны основные методики логико-вероятностного анализа. Согласно им, для дальнейших рассуждений наиболее оптимальным будет использование логико-вероятностного метода для восстанавливаемых систем.

Для обеспечения корректности суждения правомерности дальнейших суждений, необходимо наложить на систему ряд ограничений:

• 1)    совокупность элементов системы x i может обладать только одним из двух несовместных состояний: работоспособность либо отказ. Каждый из элементов представляет собой бинарную переменную, принимающую два значения: x i =1 в случае работоспособности элемента и x i =0 в случае выхода элемента из строя. Такое же ограничение бинарности накладывается на саму систему;

• 2)    совокупность бинарных событий является независимой, то есть показатели надежности одного элемента не изменяются даже в случае отказа других элементов в составе системы;

• 3)    выполнение процессов, связанных с восстановлением элементов системы, не имеет ограничений. Это подразумевает отсутствие изменений значения RTO каждого из элементов системы вне зависимости от возникновения отказов других элементов;

• 4)    законы, согласно которых осуществляется распределение случайного времени безотказной работы, а также восстановления всех элементов, считаются экспоненциальными. В случае систем массового обслуживания, указанное ограничение не носит характер грубого;

• 5)    все вероятностные характеристики структурных элементов системы носят статистически устойчивый характер, подразумевая отсутствие изменений в параметрах распределения элементов в рассматриваемый интервал времени;

• 6)    в случае, когда имеется состояние системы, при котором она неработоспособна, то возникновение сбоев оставшихся в работе элементов не сможет привести систему в работоспособное состояние.

Сейчас в различных источниках можно найти большое количество моделей, связанных с выполнением расчета основных показателей надежности вычислительных систем и сетей. Но эти модели опираются на использование восстанавливаемых элементов, что фактически не отражает специфики функционирования систем обработки данных с различными показателями интенсивности отказов при различных режимах функционирования узлов, а также различное время выполнения подключения резервного узла.

С учетом вышесказанного следует осуществить разработку специализированной модели демонстрации уровня надежности кластера высокой готовности, а также выведения расчетных формул показателей надежности и готовности системы. Рассмотрение следует начать с упрощенной модели надежности дублированной системы. В данной модели показатель надежности дублированной системы позволяет осуществлять рассмотрение узлов обработки данных в виде простейших восстанавливаемых элементов, обладающих двумя состояниями – работоспособен и неработоспособен (рисунок 2). Отказы работоспособного узла возникают с интенсивностью λA, в результате чего узел переходит в неработоспособное состояние. Восстановление неработоспособного узла происходит с интенсивностью μN, в результате чего узел переходит в работоспособное состояние.

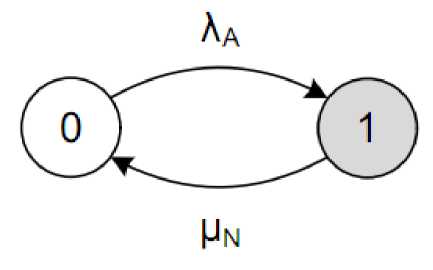
Рисунок 2 – Граф состояний узла с двумя состояниями

Получается фактически, что данная система является дублированной системой с независимыми узлами. Это означает что каждый узел может находиться в одном из двух состояний независимо от состояния другого узла, а сама система считается работоспособной в тот момент времени, когда работоспособен хотя бы один из входящих в её состав узлов. Помимо этого, одни и те же запросы данных могут быть обработаны обоими узлами в случаях, когда они одновременно являются работоспособными. Далее следует рассмотреть множество состояний данной системы:

Состояние 0 возникает, когда оба узла являются работоспособными и могут обрабатывать поступающие запросы пользователей. Из данного состояния система на основании интенсивности 2λ A , подразумевающего отказ одного из узлов, осуществить переход в состояние 1.

Состояние 1 возникает в момент, когда только один из узлов находится в работоспособном состоянии, а второй узел, соответственно, в неработоспособном. Из данного состояния системой может быть осуществлен переход в состояние 2 с интенсивностью отказа работоспособного узла λ A , либо перейти в состояние 0 на основании интенсивности восстановления неработоспособного узла μ N .

Состояние 2 возникает, когда оба узла находятся в состояния неработоспособности, и соответственно система тоже неработоспособна. Из данного состояния система с интенсивностью восстановления одного неработоспособного узла 2μN может выполнить переход в состояние 1.

На основании вышесказанного получается граф, представленный на рисунке 3

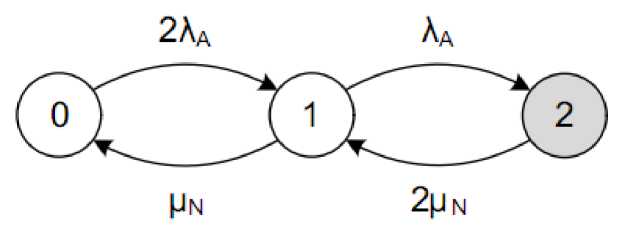
Рисунок 3 – Упрощенная модель надежности дублированной системы

Аналитическое решение для получения формул стационарных вероятностей всех описанных состояний при установлении Марковского процесса будет представлено в следующем виде [1]:

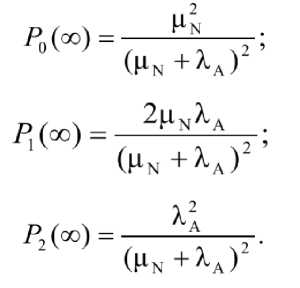
На основании данных формул можно представить формулу готовности дублированной системы с учетом обработки запросов пользователей системой при нахождении её в состояниях 0 и 1:

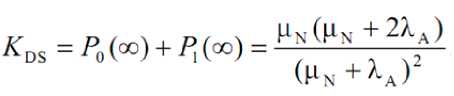
В случае необходимости выполнения расчетов конечного времени при подключении резервных узлов, а также необходимости подсчета различных интенсивностей отказов узлов в нагруженном и ненагруженном режиме работы следует применить усовершенствованную модель системы, в которой узлы представлены элементами с тремя состояниями: пассивный, активный и неработоспособный (рисунок 4). В данной модели если узел в состоянии «активный», то он осуществляет обработку запросов пользователей. В случае если узел находится в состоянии «пассивный», он с интенсивностью λP отказывает и осуществляет переход в неработоспособное состояние, либо с интенсивностью γN переходит в активное состояние. Узел из активного состояния переходит в неработоспособное состояние с интенсивностью λA. Восстановление неработоспособного узла осуществляется на основании интенсивности μN, после чего он переходит в пассивное состояние.

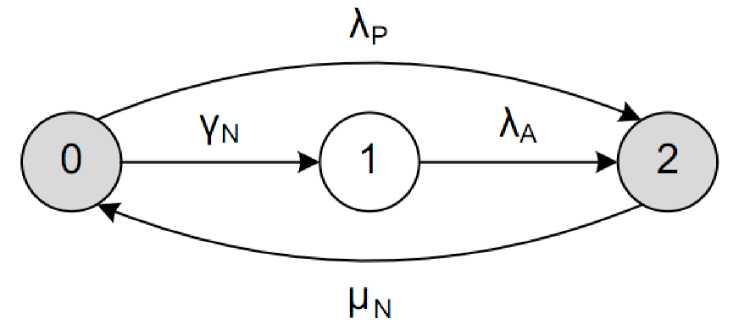
Рисунок 4 – Граф состояний узла с тремя состояниями

Согласно данной модели предполагается, что в данной системе в определенный момент времени только один узел может находиться в активном состоянии, осуществляя обработку запросов пользователей и имея доступ к общей базе данных. А так другой узел находится в пассивном состоянии, то только один из них может быть переведен в активное состояние. Для упрощения модели будет принято, что каждый узел независим от остальных по отказам и восстановлениям. Далее необходимо рассмотреть множество всех состояний системы:

В состоянии 0 оба узла являются работоспособными и находятся в пассивном состоянии. Из данного состояния системой может быть выполнена активаций одного из узлов для перехода в состояние 1 с интенсивностью γ_N, либо может произойти отказ любого из двух пассивных узлов и переход в системы в состояние 2 с интенсивностью 2λ P .

В состоянии 1 оба узла являются работоспособными, но только один в активном состоянии, а второй в пассивном состоянии. Из данного состояния возможен отказ активного узла и переход системы в состояние 2 с интенсивностью λ_A, либо осуществление отказа пассивного узла и переход системы в состояние 3 с интенсивностью λ P . Причем в данном состоянии система может выполнять обработку запросов пользователей.

В состоянии 2 один из узлов системы является неработоспособным, а другой – работоспособным, но в пассивном состоянии. В данном случае возможна активация пассивного узла и переход в состояние 3 с интенсивностью γ N , в случае отказа пассивного узла система переходит в состояние 4 с интенсивностью λ_P, либо может произойти восстановление неработоспособного узла, и система перейдет в состояние 0 с интенсивностью μ N .

В состоянии 3 один из узлов является неработоспособным, другой является работоспособным и активным. Из данного состояния в случае отказа активного узла система переходит в состояние 3 с интенсивностью λ_A, либо при восстановлении неработоспособного узла переходит в состояние 1 с интенсивностью μ N . В данном состоянии система может выполнять обработку запросов пользователей.

В состоянии 4 оба узла в составе системы находятся в неработоспособном состоянии. Из данного состояния может произойти только восстановление любого из двух неработоспособных узлов с интенсивностью 2p N , что приведет к переходу системы в состояние 2.

На основании вышесказанного будет получен граф состояний, представленный на рисунке 5.

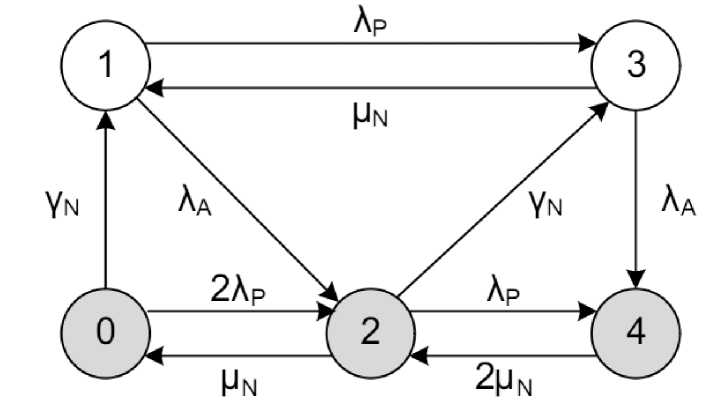
Рисунок 5 - Модель надежности систем с основным и резервным узлом

Таким образом, с учетом того факта, что обработка пользовательских запросов осуществляется только тогда, когда система находится в состояниях 1 и 3, стационарный коэффициент готовности будет рассчитываться по формуле [3]:

K_V?=PW-P_;№ (3)