Построение модели надежности системы

Прожиточный_минимум

URL:

URL:Уровень_бедности

ЮРГПУ(НПИ)

Россия, г. Новочеркасск ПОСТРОЕНИЕ МОДЕЛИ НАДЕЖНОСТИ СИСТЕМЫ

В статье изложена процедура количественной оценки качества проектного варианта на этапе структурного синтеза системы. Предложена системная модель надежности системы, позволяющая повысить достоверность расчета показателей надежности системы.

Надежность системы является комплексным свойством, формируемым на всех стадиях её жизненного цикла. На стадии проектирования актуальной задачей является формирование модели надежности системы, обеспечивающей достоверность рассчитываемых показателей надежности [1] . В статье излагается вариант решения этой задачи.

Логическая взаимосвязь проектных операций при формировании надежности отражается моделью надежности:

P: < MO, D >, где - P номенклатура показателей надежности;

M O – множество объяснительных моделей системы;

D - множество моделей отказов.

В свою очередь объяснительная модель определяется следующим образом:

MO = < S, V, SD >, где    S = {sk} - множество символических моделей описания функционирования системы.     В качестве символических моделей используются    функциональные,    структурные,    принципиальные, мнемонические и другие виды схем и образов, поясняющих функционирование системы;

V – множество свойств надежности.   Множество V составляют свойства, раскрывающие комплексность надежности;

S D – множество свойств отказов.

Множество моделей отказов D = < F, A >, где

F – множество моделей расчета показателей надежности;

A – множество методов измерения ( оценки) надежности системы по надежности её базовых элементов.

В статье рассматривается построение моделей надежности на основе методологии функционального моделирования IDEF0 [2].

Модель IDEF0 есть иерархия уточнений описания функционирования системы. Структура уровней описания приведена на рис 1

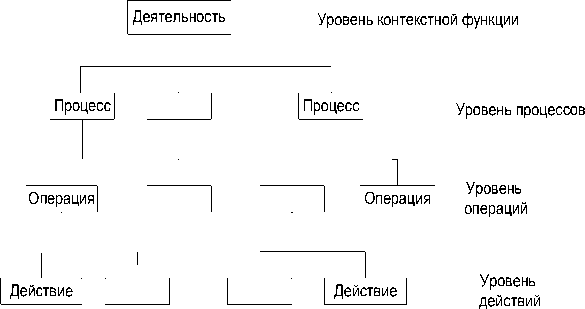
Рис. 1. Иерархия уровней описания в модели IDEF0

Основным символом графической модели для представления функции служит поименованный прямоугольник. Агломеративную функцию называют диаграммой. Любая диаграмма может быть декомпозирована на составляющие её блоки (4-6 блоков). Связи между блоками (диаграммами) обозначаются стрелками. Стрелки отражают конкретное содержание информационных, материальных, энергетических потоков, обеспечивающих реализацию деятельности.

Для количественного описания содержания связей следует ввести спецификации стрелок [3]. В спецификациях стрелок отражают: -переменные, определяющие количественные характеристики потоков; ограничения на них в форме «законов сохранения», выражающие системные особенности функционирования структуры, а также условия возникновения отказов. Пример возможной структуры спецификации представлен в форме таблицы № 1

		Таблица №. 1
Идентифи	Состав	Ограничения		структурные	Условия
катор	(переме			параметры	отказа
стрелки	нные)	информ	материал	энерге        b ii       a jl
		а	ь	тические
		ционны	ные

е

Если в стрелке содержится несколько составляющих, то в условиях отказа записывается логическое высказывание об их взаимодействии, приводящем к её отказу.

Следовательно, построенная IDEF0 модель может рассматриваться как объяснительная модель функционирования системы - M O .

Для построения модели отказов D системы введем оператор преобразования R = R ( St; L), где

St – оператор описания структурных свойств диаграммы;

L - модели отказов.

В качестве аргументов оператора St выступают следующие структурные характеристики модели: Φ – множество уровней модели; матрица B_f = [b_fil] – характеризует связность контактов внутренних блоков с соответствующими внешними контактами f - ой диаграммы (V il ); J – множество бинарных векторов. Единичные компоненты бинарного вектора J f-1 определяют блоки диаграммы, подлежащие декомпозиции; структурный вектор N =(n 1 , n 2 ,….,n k ), где n f – число блоков в f – ой диаграмме; ∑ f = [s fij ] – структурный конфигуратор f – ой диаграммы, описывающий характер связности внутренних её блоков, элемент s ij определяет способ соединения блоков в диаграмме.

Структурные параметры s ij определяют прямые связи (при j > i) контакта 3 (выхода) блока i с контактами 1, 2,4 блока j внутри диаграммы IDEF0- модели, параметры s ij ( при j

S ij = (^a j , a ij2, 0, a ij ₄ ) , где _Q < a _ijt <  1, . = . = (1 ^ n f ),  i = (1 ^ 4);

b i = ( bn, b_t 2 , b_i3, b_i4).

Параметр  αijl   в общем случае является количественной оценкой содержания спецификации соответствующей стрелки.

Укрупненные показатели связности блоков в диаграмме :

• -    связность выхода i-го блока с l –ми контактами блоков в пределах ∑ ^α ijl

рассматриваемой диаграммы - c il =    ^{j ≠ i .}      ;

∑ ^α kil

• -    связность l-го контакта i-го блока с выходами блоков - c li = ^{k ≠ i}    ;

• -  r_i = (c_1i,c_2i ,0,c_4i ) – вектор, характеризующий связность контактов i –

го блока с выходными контактами остальных блоков диаграммы;

• -    ŕ_i = ( c_i1; c_i2; 0_; c_i4) - описывает связность (нагрузку) выхода i – го блока с контактами других блоков этой диаграммы. При этом прямые связи описываются вектором ŕ i ⁺ = (c i1⁺ ,c i2 ⁺ ,0, c i4 ⁺ ), обратные связи - вектором ŕ i ^- = (c_i1 ,c_i2 ,0, c_i4 ) .

Для анализа структурных особенностей системы положим α ijl = 1 и b il =1. Тогда для связей «выход-вход; выход-управление; выход-механизм исполнения; выход - обратная связь на вход; выход - обратная связь на управление » векторы ŕ i будут иметь вид: ŕ i⁺ = (c i1⁺ ,0,0, 0); ŕ i ⁺ = (0, c i2⁺ ,0, 0); ŕ ⁺ = (0, 0,0, c i4 ⁺ ); ŕ i ^- = (c i1^- ,0,0, 0); r i^- = (0, c i2 ^- ,0, 0).

На этапе построения модели отказов L целесообразно использовать метод построения дерева отказов [4]. Модель отказов можно представить, как тройку:

L = < St; B; F>, где -B – множество деревьев отказов диаграмм модели IDEF0;

F – множество булевых функций

Построение деревьев отказов начинают «снизу – вверх». Родительская диаграмма блока операционного уровня заменяется в дереве отказов событием, описываемым дизъюнкцией (конъюнкцией) отказов дочерних действий. Такая последовательность объединений распространяется до вершинного события.

При построении модели L, основываясь на принятой в анализе бизнес-процессов идее выделения горизонтальной и вертикальной составляющих деятельности организациями [5], будем рассматривать горизонтальную («вход» - «выход») и вертикальную («управление» и «исполнение») составляющие работоспособности системы.

Для обоснования события – отказ диаграммы по направлению «вход-выход» рассматриваем событие – отказ выходной стрелки диаграммы. Формирование этого события предусматривают следующую последовательность операций:

• -    анализ вектора r i^.+ .   В случае если все вектора r i⁺ имеют вид r i⁺ =

(1,0,0,0), то отказ диаграммы следует в дереве отказов связывать дизъюнкцией отказов выходных стрелок блоков данной диаграммы, так как её функционирование возможно, лишь при наличии «предметов- стрелок» на входах блоков;

• -    если характер связей имеет вид r_i ⁺ = (c_i1 ⁺ ,0,0, 0), то формируют вектор B l = (b_1l, b_2l,., bn? l ), характеризующий связь контакта l диаграммы с одноименными контактами блоков этой диаграммы и S il⁺ = ( α i(i+1),l ; α (i+1), (i+2),l ; • ■ -^(n f -iyrt f ,1; ^b n f ,3 ^).

Так как блок с номером 1 доминирует все остальные блоки диаграммы, то анализ следует начинать с векторов B 1 , B 3 и S 1l⁺ .

При числе единичных компонент в векторе B 3 ≥ 2 находят покоординатное произведение П = B 1 * B 3 * S 11⁺ . При единичных компонентах вектора S 11⁺ определяют номера блоков (k), для которых компоненты вектора П равны 1. Блоки, расположенные между последовательными единичными компонентами вектора П, соединяются последовательностью (путём) выходных стрелок Отказ, хотя бы одной стрелки в таком пути, приводит к отказу выделенной последовательности блоков. В дереве отказов описанная ситуация отражается родительским событием, связанным дизъюнкцией с входными событиями – отказами выходных стрелок соответствующих блоков.

Количество путей, содержащихся в векторе П, определяет число родительских событий в диаграмме. При этом событие, соответствующее отказу диаграммы, формируются как конъюнкция найденных родительских событий.

При b i3 = 0, b 23 = 0,..., bn_f з = 1 и Ьц = 1, b 2 = 0,..., bn_f 3 = 1 анализируют структуру вектора S_1l + = ( a _1l, a ₂₁ , .,x _n/-1 , ₁,b_nf ,3 ). Событие, соответствующее отказу диаграммы, определяется как дизъюнкция отказов стрелок, соответствующих единичным компонентам вектора S 1l⁺ .

Если в векторе В 1 имеется несколько единичных компонент, то находят произведение П₁ = B₁ * S_1l ⁺ , определяют путь из стрелки b₁₁ и компонент вектора S 11⁺ до блока (i), соответствующего второй единичной координате П 1 , составляют дочернее событие, определяемое конъюнкцией отказа стрелки b_i1 с дизъюнкцией отказов компонент, входящих в сформированный путь. Если на входе некоторого блока, входящего в путь, действует стрелка обратной связи по входу, то формируется конъюнкция отказов стрелок обратной связи и компоненты из S 11⁺ . Построенное таким образом событие входит в путь до следующей единичной компоненты П 1 . Описанным выше способом определяют второе дочернее событие и т. д. Отказ диаграммы находят как дизъюнкцию найденных дочерних событий.

Поскольку блок с номером 1 является доминирующим в диаграмме, то можно ограничиться этим случаем.

Построение дерева отказов для оценки надежности по «исполнению» и «управлению» .

Рассмотрим первый блок диаграммы. Условием его функционирования с точки зрения управления является наличие на втором его входе («управление») стрелок от второго входа диаграммы (b12) , стрелок прямых связей по управлению c21+ и стрелок обратных связей по управлению c21- от блоков этой диаграммы.

∑ α kil ∑ ^α ijl

Так как - c 21 = ^{k ≥ i} ; c 21 ^- = ^{j < i .} ; то отказ диаграммы по управлению в дереве отказов отражается событием, формируемым конъюнкцией отказов стрелки b_12, стрелок, соответствующих единичным компонентам в c 21⁺ и c 21 ^– .

В случае необходимости учета отказов по «управлению» других блоков данной диаграммы, событие, определяющее её отказ, рассматривается как родительское, дочерними событиями которого являются отказы блоков, определяемые по аналогии с первым блоком. При этом отказ диаграммы определяется конъюнкцией дочерних событий.

Для построения события – отказ диаграммы по «исполнению» рассматривают аналогичное описание относительно четвертого входа ( «исполнитель» ) диаграммы. При этом используются стрелка (b 14 ), стрелки прямых связей по исполнению (c 41⁺ ) и стрелки обратных связей по исполнению (c 41^- ).

Приведенная процедура построения дерева отказов родительской диаграммы инвариантна относительно уровня модели и позволяет построить булеву функцию для всей модели в целом. По полученной функции, используя логико- вероятностные методы расчета показателей надежности, определяют вероятность отказа системы.

Таким образ, использование моделей M O = < S, V, S D >, L = < St; B; F> позволяет реализовать системный подход в расчетах надежности, что повышает достоверность определения показателей надежности проектного варианта системы.