Построение модели солнечной радиации на основе наземных наблюдений на примере данных по Иркутску

Постановка задачи. Эффективность применения солнечных энергетических систем, как тепловых, так и фотоэлектрических, во многом определяется точностью оценки энергетических ресурсов, свойственных данному району.

При анализе приходящей солнечной радиации необходимо учитывать три основных фактора: астрономическую инсоляцию, географическое расположение и климатический фактор.

Функция астрономической инсоляции от времени есть детерминированная функция и может быть найдена на основании известных методов, например, изложенных в работе. Но в реальных условиях радиация, приходящаяся на поверхность приемных панелей солнечных энергетических систем, будет иметь значительные отличия от расчетных значений астрономической инсоляции.

Влияние состояния атмосферы и отражающих свойств окружающих поверхностей приводит к тому, что глобальная солнечная радиация, которая является суммой прямой, диффузионной и отраженной радиации, будет представлять собой случайную функцию времени - стохастический процесс. В этом случае построение модели для оценки энергетического потенциала глобальной солнечной радиации возможно на основе статистического анализа многолетних метеорологических наблюдений.

Исходиые данные для построения модели. Из доступных данных наземного наблюдения по Иркутской области имеется ряд наблюдений глобальной и диффузионной солнечной радиации, проводимых метеостанцией, с международным индексом 30710 и расположенной в точке с координатами 52° 16' северной широты, 104°2Г восточной долготы. Данные получены с сайта Мировой Центр Радиационных Данных (World Radiation Data Centre). После исследования целостности данных по глобальной радиации было установлено, что для дальнейшего анализа пригодны данные за следующие периоды: 1964-1990 гг. и 2007-2011 гг. В данных за период с 1991 по 2006 год имеются значительные пропуски, что делает их непригодными для решения поставленной в данной работе задачи. Из имеющихся данных по диффузионной радиации пригодными для анализа оказались данные по следующим шести годам наблюдения: 1991, 1992, 2007, 2008, 2010 и 2013 годы.

В исходном виде данные представляют собой результаты измерения солнечной радиации с помощью пиранометра. Размерность исходных значений ДЖ/см2 пересчитана на размерность 13тч/м7

В дальнейшем массив данных глобальной радиации обозначается в работе как матрица G и имеет размерность 365x32, массив данных диффузионной радиации обозначен в работе как матрица D и имеет размерность 365x6. В графическом виде исходные данные представлены на рисунке 1.

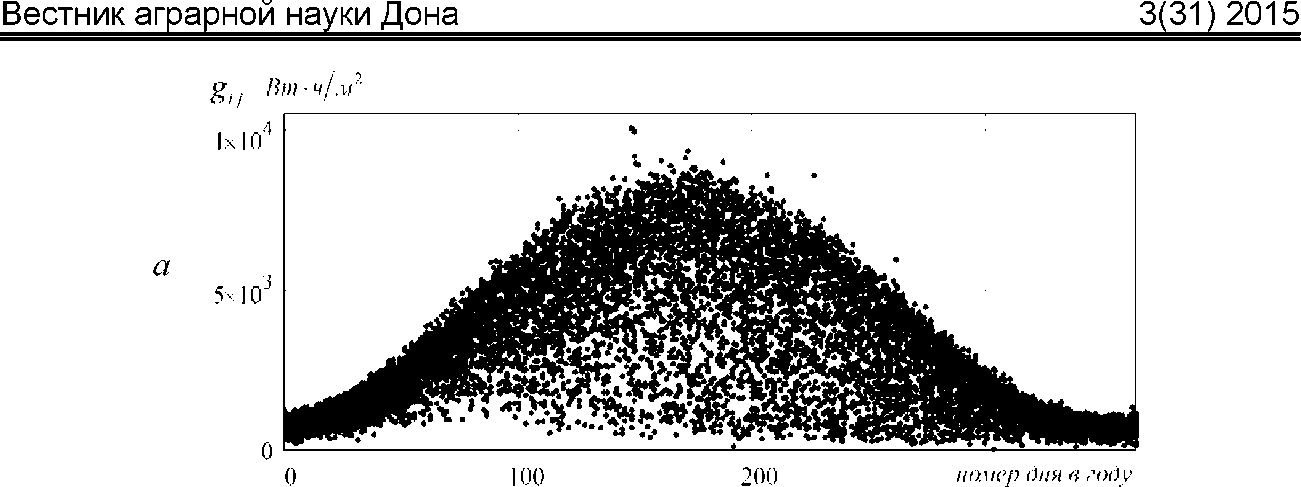
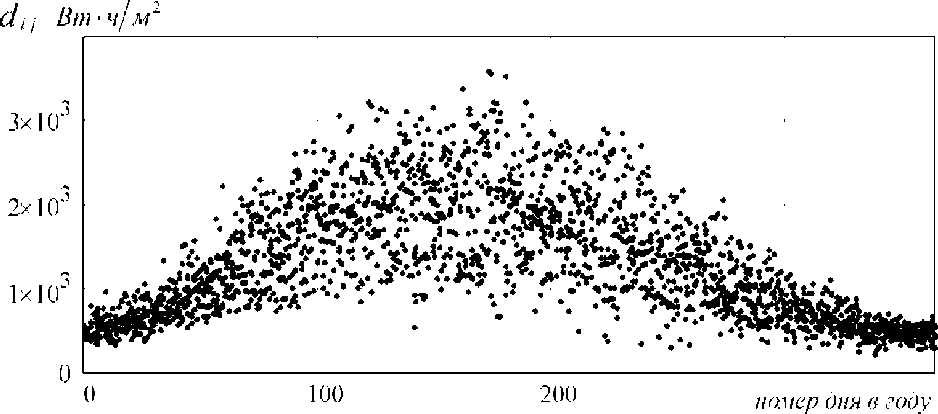
a - отображение массива измерений глобальной радиации G с элементами g_t,, где I - номер дня в году, / - номер столбца, соответствующий одному из годов наблюдений; б - отображение массива измерений диффузионной радиации D с элементами d._{; s} где / - номер дня в году, j - номер столбца, соответствующий одному из годов наблюдений

Рисунок 1 - Графическое представление исходных данных для построения модели солнечной радиации

Методика построение модели* Основной целью построения модели солнечной радиации является создание удобного инструмента для оперативной оценки энергетического ресурса солнечной энергии в заданном районе. Исходя из этой цели, авторами была разработана нижеизложенная методика построения модели солнечной радиации.

Первым этапом анализа является вычисление оценок математического ожидания и среднеквадратичного отклонения для каждого /-ого дня наблюдаемого периода:

|         Ng _ у firs                                       j          Nd _ vcw.s¹

g mean=------- V g,,,d mean.=------- V d; ,

Ag _ yars ”^              Nd _ yars

АУ уo.rs                            _?

g stdev = /-------- V Ng _yai

7 E Uy-8_meany ,

1 7=1

d _stdevl =

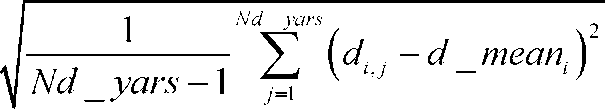
На втором этапе построения модели производится аппроксимация полученных на предыдущем этапе векторов среднего значения G_mean, D_mean и среднеквадратичного отклонения Gstdev, Bstdev аналитическими выражениями. Проведенные ранее исследования показали, что одним из наиболее приемлемых вариантов аппроксимирующей функции является использование тригонометрических рядов, в частности ряда Фурье. Количество членов ряда в конечном счете определяется необходимой точностью аппроксимации и, как показывает практика для ряда Фурье, волне достаточно девяти членов:

^(z) = a + ^b_k cos^k® i) + ^c_k sin (Ату /)' ^ а 1 k 1

где / - номер дня в году, o — ^N—l)/^ - частота первой гармоники, N-365 - число дней в году, 366 день в високосный год при расчетах не учитывался.

В результате необходимо получить 4 аналитические функции ^^^а_тест (О’ о«™.ДД °^а^Д6 ^"^('У ^аппр°^к-симирующие векторы оценок среднего значения и среднеквадратичного отклонения.

Третий этап построения модели имеет целью построения границ доверительных интервалов, позволяющих пользователю получить статистическое обоснование при расчетах ожидаемого прихода солнечной энергии. В случае нормального распределения эта задача имела бы простое решение. Но как показывают результаты предыдущих исследований, распределение в сечениях (по дням) имеет негауссовский закон, более того это распределение имеет несимметричную форму относительно среднего значения. Эти факторы значительно осложняют определение границ доверительных интервалов, поэтому авторами был разработан подход, позволяющий произвести их оценку эмпирическим методом на основе имеющихся массивов данных.

В силу несимметричности распределения значений имеет смысл рассмотреть два подхода к построению границ доверительных интервалов: равновеликий и рав новероятностный. В силу ограниченного объема данной работы рассмотрим первый наиболее простой способ построения равновеликих доверительных интервалов.

При равновеликом подходе границы доверительных интервалов располагаются равноудалено от среднего значения. Верхняя и нижняя граница доверительного интервала будет определяться выражениями:

⁽д (0=^Ga„,_m„ (0+^ •^Ga^. (О ’

^Gk„er (0 = ^Gam«™ (') ^{+ Ь Ga}«d«v (') ’ к^ор (') = ^Dam„„ (') ^{+ k} ' ^D«sti_cv (')’

(0 = ^Da„_E™ (0 + ^k • Da„_d6v (/). (4)

Каждый из массивов исходных данных G и D разделяется на два массива соответственно: Gin, G out и D in, B out. Элементы массивов G in и D in соответ ственно удовлетворяют условиям:

Элементы массивов G и /J), которые не удовлетворяют этим условиям, переносятся соответственно в массивы G out и Bout

Введем следующие обозначения: NG - количество элементов в массиве данных G, ND - количество элементов в массиве данных D, NGi_n - количество элементов в массиве данных G in, ND^_n - количество элементов в массиве данных B in и определим эмпирическую вероятность попадания исходных значений в интервал, определенный верхней и нижней границей (3)и(4):

Р р s NG ’ ND

Границы доверительного интервала определяются следующим образом. Задается необходимое значение доверительной вероятности Р₈ (или Ра) и варьированием коэффициента к в выражении (3) (или (4)) добиваются выполнения необходимого условия (6).

Результаты и обсуждения. Рассмотрим применение предложенной выше методики на примере данных измерения солнечной радиации в Иркутске. Результаты вычисления оценок среднего значения и среднеквадратичного отклонения для глобальной и диффузионной радиации по формулам (1) приведены на рисунке 2.

Вычисление коэффициентов аппроксимации были выполнены методом наименьших квадратов, результаты вычисления приведены в таблице. Точность аппроксимации оценена на основе коэффициентов детерминации - р2, во всех четы рех случаях выполнено условие р2> 0,96, что указывает на высокую точность.

На рисунке 2 приведены полученные аппроксимирующие кривые и показаны границы некоторого доверительного интервала, построенные как на основе аппроксимирующих выражений, так и на основе оценок среднего значения и среднеквадратичного отклонения.

Значения коэффициентов аппроксимации для аппроксимирующих гармонических рядов

Коэф-фици-ент Значение коэффициента аппроксимации Ga«aA^ ^х/^СО а 8192.582653 -457.3 52020 1317.497067 1127.190012 bi -104.522118 -434.577858 515.508593 8 34.91419390 ь2 -7865.57420 807.9594209 -34.7122991 -1371.13480 Ьз 80.21574567 408.9113 65 8 -792.93 8272 -1109.86546 Ь4 446.3048507 -154.532089 -413.268246 0.645603 508 Ci -8703.52858 2754.060112 -475.892132 -30.8791177 С2 839.8291889 594.4436967 64.22716229 390.4101483 с? 2424.3 5163 3 -850.333972 -36.8005276 76.55472835 С4 -93 8452516 -120.585438 156.1283247 17.05943187 а - для массива значений глобальной радиации;

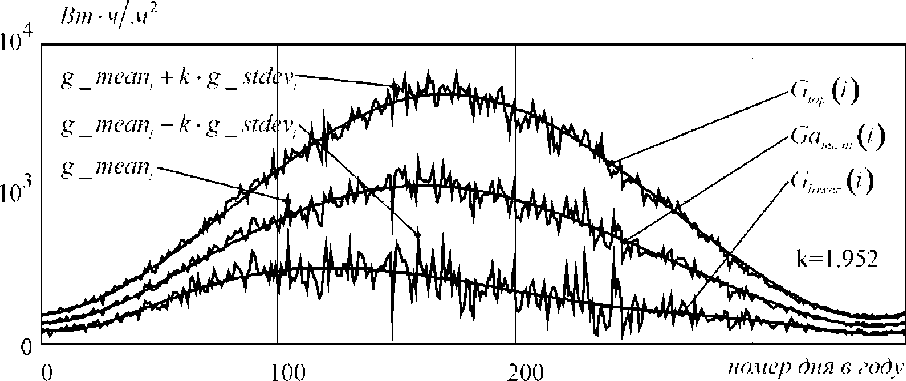
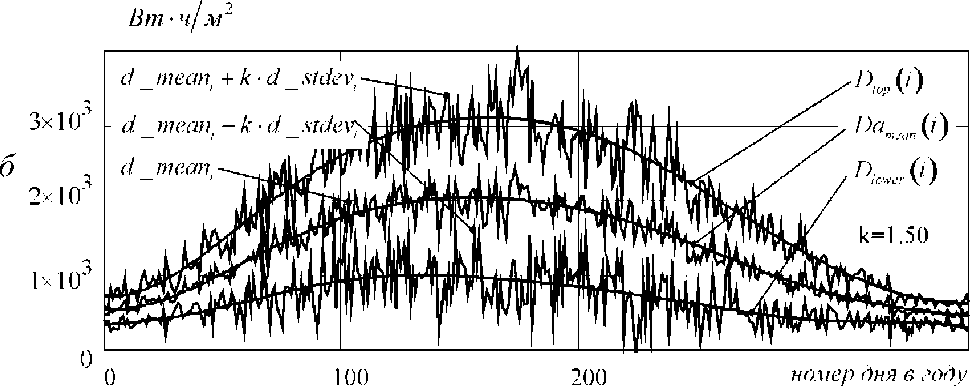
б - для массива значений диффузионной радиации Рисунок 2 - Оценки среднего значения и среднеквадратичного отклонения, аппроксимирующие функции и границы доверительного интервала

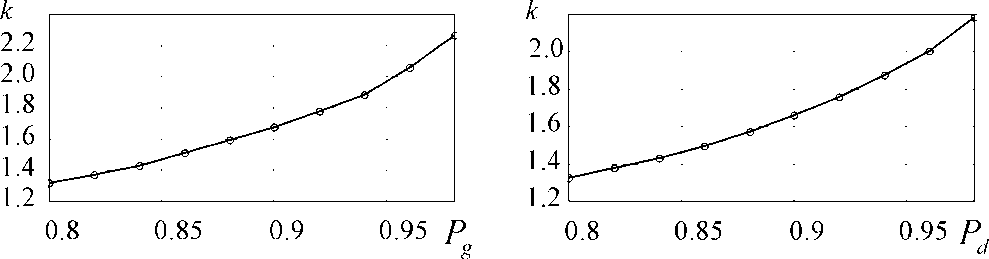
Рисунок 3 — Зависимость значения параметра к (в выражениях (3) и (4)) от заданного значения доверительной вероятности

Полученные на предыдущих этапах результаты позволяют перейти к вычислению границ доверительных интервалов. Опуская технические подробности процедуры нахождения значений параметра к в выражениях (3) и (4) при заданных значениях доверительной вероятности, приведем результат этих вычислений в виде графиков на рисунке 3.

В результате проведенных вычислений были получены статистические модели для оценки значений глобальной и диффузионной солнечной радиации для Иркутска. Задаваясь необходимым значением доверительной вероятности, пользователь может определить границы доверительного интервала, используя выражения (3) и (4), а также графики, приведенные на рисунке 3.

Заключение. В заключение рассмотрим основные проблемы применения данной модели на практике и пути её дальнейшего развития. Первое, что необходимо отметить, это недостаточное количество данных для проведения вычислений. Особенно это заметно для данных по диффузионной радиации. Из всего набора данных пригодными оказались только данные за шесть лет наблюдения. Соответственно и полученные оценки среднего значения и среднеквадратичного отклонения имеют большую дисперсию. Также негативно это сказалось и на определении границ доверительных интервалов. Основным путем решения этой проблемы является привлечение иных источников данных по солнечной радиации. В настоящее время авторы исследуют возможность использования данных из проекта NASA SSE.

Вторым недостатком рассмотренной модели является использование равновеликих доверительных интервалов. Как уже указывалось ранее, эмпирическое распределение в сечениях (по дням) имеет несимметричную форму, и, следовательно, здесь более корректным является использование равновероятностных доверительных интервалов. Дальнейшим развитием модели может стать раздельный расчёт доверительных интервалов по сезонам и месяцам.

И в заключение необходимо отметить, что применение модели может стать значительно удобнее при её реализации в виде программного комплекса, что избавит пользователя от необходимости самостоятельного проведения расчетов.

Сведения об авторах