Построение мульд сдвижения дневной поверхности месторождений, полученных расчётным методом по единичным данным геодезических измерений и материалам многолетней разработки крупных газовых залежей (на примере пласта ПК-1 сеномана южной части Губкинского месторождения)

Теоретическое обоснование. Явление оседания земной поверхности при добыче углеводородных флюидов хорошо известно в мировой практике. Опыт исследований этого явления показывает, что мульда сдвижения может иметь самые различные характеристики (прямые оседания поверхности от сантиметров до нескольких метров, воронкообразные формы оседаний с различными радиусами влияния, ложно карстовые воронки и т.п.) в зависимости от физикомеханических свойств вмещающих пород и литологии нефтегазовых коллекторов. В результате этих оседаний многие инженерные сооружения и даже природные объекты терпят значительный ущерб [1, 4, 6, 10, 11,], который можно минимизировать научно -методическими принципами размещения объектов на основе концепции геодинамической безопасности.

Обработка и анализ информации о влиянии темпов разработки месторождения на геодинамическую безопасность наземных и подземных (промышленных и гражданских) зданий и сооружений уже в настоящее время и, особенно для последующих лет эксплуатации углеводородных залежей, как прогнозно-техническое направление становится весьма актуальным.

Из материалов разработки Губкинского газового месторождения анализировались карты толщин слоев 0, 1, 2, 3 горизонта ПК 1, схемы отбора газа, карты толщин подъема газо-водяного контакта (ГВК) и карты падения пластового давления. Для удобства расчёта, исходя из основных данных разработки месторождения за 10 лет (период с 2000 по 2010 годы) по полученным цифровым значениям каждого года построены математические схемы расчетных мульд сдвижения дневной поверхности 2008, 2009 и 2010 года.

Замкнутые фигуры мульд оседания по нулевым значениям построены комплексацией методов: расчетом деформации горного массива по упругой модели; интерполяцией нулевых точек пласта по структурно -тектоническому плану; анализом начального положения ГВК пласта ПК-1 южного участка; а также по- строением математической модели компьютерного варианта.

В основу способа расчетного варианта мульды положена послойно-блочная упругая модель горного массива, в которой поведение пород под нагрузкой зависит от времени разработки, темпов добычи сырья и структуры пород. Предполагается, что внутри массива появляются объемы с пониженным пластовым давлением, в которых от веса вышележащей толщи нагрузка не превышает предел прочности пород, где возникают исключительно упругие деформации. Последние, не зависят от времени и, в соответствии с законом Гука, развиваются прямо пропорционально нагрузке (рис. 1.).

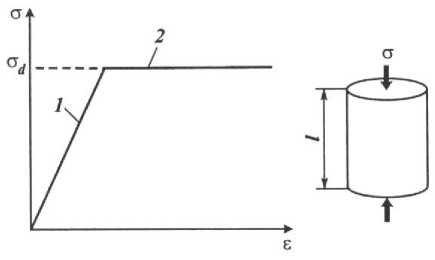
Е=Д1/1

Рис. 1. Деформирование изотропной горной породы (1 -упругие деформации; 2 - пластические деформации; 1 - высота образца).

При описании упругих деформаций пород исходят из моделей их структурного состояния. Для пород с неориентированной зернистой структурой возникающие упругие деформации не зависят от направления действия нагрузки. В этом случае для описания напряженно-деформированного состояния достаточно двух констант материала: модуля упругости Е и коэффициента Пуассона v , так как модуль сдвига можно выразить через Е и v . G=E / [2(1+v)]. В соответствии с законом Гука напряжения и деформации в произвольной декартовой системе координат (х, у, z) можно связать между собой следующими соотношениями:

E стг =--------4(1 - v )£ + v£ + v£z ];

• ¹   1 - v - 2 v ^2LV ’ x     y     ¹¹

E

°y = i-----Гт[ v£x+ (1 - v )£y+ £];

• 1    - v - 2 v

E

az =;-----7т[ v£x+ v£y+ (1 - vК];

• 1    - v - 2 v

E

^T x ^y = 2(1 + v ) ^{Y xy} ’

E

^{T yz} = 2(1 + v ) ^{Y yz} ;

E

T zx =          Yzx .    (1)

2(1 + v )

Для схематизированного строения породы со слоистой структурой допущение об моноизотроп-ном характере ее деформаций чаще всего недопустимо [3, 4]. Как показывает опыт, сжимаемость слоистых пород в направлении, нормальном к напластованию, заметно больше, чем в направлении, параллельном этой плоскости?

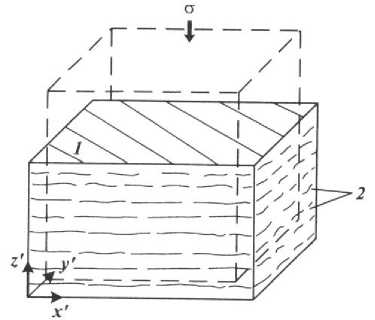
Рис. 2. Анизотропная деформация горной породы со слоистой структурой (1- плоскость изотропии; 2 – слоистость).

Для таких пород напряженно-деформированное состояние описывается с помощью модели прямолинейно-изотропного упругого тела. Для этого необходимо пять констант материала: модули упругости E 1 и E₂, характеризующие сжимаемость соответственно перпендикулярно к плоскости изотропии и в плоскости изотропии, два коэффициента Пуассона v₁ и v₂, а также модуль сдвига G 2 для напряжений сдвига в плоскости изотропии.

Предположение о том, что породы со слоистой или линейной структурой проявляют прямолинейноизотропные упругие свойства, не всегда соответствует встречающимся в природе условиям. Например, если скальная порода расчленена тремя взаимно ортогональными системами трещин, которые частично раскрыты и заполнены, то зависимость деформирования породы будет проявляться от направления действия нагрузки по динамически напряженным зонам [ 7 ].

В этом случае выявляется более высокая степень анизотропии – ортотропия. Для ее описания необходимо девять независимых констант упругости - это модули упругости Е1, Е2 и Е3 для трех взаимно ортогональных направлений, три коэффициента Пуассона v1, v2 и v3, а также три модуля сдвига G1, G2 и G3. Из теории упругости известно, что может понадобиться до 21 константы постоянной упругости для точного описания анизотропного поведения породы. Современные численные методы расчета позволяют без труда учесть в расчетах любую степень анизотропии породы. Одна- лить такое число постоянных констант упругости вряд ли возможно из-за высокой сложности и стоимости работ. Поэтому на практике чаще всего принимается в расчет упругая изотропная или прямолинейноизотропная модель горного массива.

Для достоверного прогноза параметров процесса сдвижения создается геолого-физическая модель участка месторождения, в которой отображаются основные влияющие факторы [5, 8, 12]. К ним относятся укрупненные элементы геологического разреза, представляющие собой сходные по составу и строению породные образования. Нами решается этот вопрос разломно-блочным строением [5, 7, 9].

Выбор размеров расчетной схемы определен геометрическими параметрами продуктивного пласта. Как правило, месторождения Западной Сибири имеют значительные размеры в плане (десятки километров) и средние глубины от 1 до 3 км. При таком соотношении R/H достаточно рассматривать двухмерные конечноэлементные модели, потому что в этом случае уменьшается степень влияния упругих свойств вмещающих пород на оседание земной поверхности. Для этих моделей достаточно уделить внимание обоснованию упругих и компрессионных свойств пород-коллекторов.

В качестве примера рассмотрим влияние физикомеханических свойств природного массива и коллек- ко для практических задач экспериментально опреде-

Физико-механические свойства пород

Таблица 1

Тип породы	Мощность слоя, м	Модуль упругости, МПа	Коэффициент Пуассона	Объемный вес породы МН/м3
1. Чередование песков, суглинков, глин	100	1500	0,35	0,019
2. Глинистые толщи	150	5000	0,3	0,02
3. Переслаивание глин, аргиллитов	300	7500	0,3	0,022
4. Глинистая толща	100	5000	0,3	0,02
5. Чередование песков, алевролитов, глин, песчаников	110	3500 ± 1000	0,35	0,021

тора на величину оседания дневной поверхности при разработке пласта ПК-1 сеномана. Расчетные слои

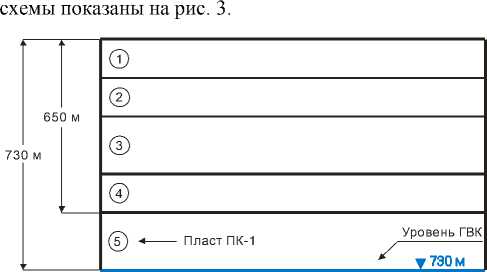
Рис 3. Расчетная схема прогноза сдвижений и деформации горного массива при разработке пласта ПК₁ (1 слой - чередование песков, суглинков и глин четвертичного возраста; 2-суглинки и глины миоцен-олигоцена; 3-глины и аргиллиты глубокого моря; 4-глины литорали теплого моря; 5 -чередование песков, алевролитов, глин и песчаников сеноманской толщи).

Далее задаем размер модели таким образом, чтобы получить участок плоского дна мульды сдвижения, т. е. оценить максимальное оседание поверхности. В структуре выделяем участок толщи (геоблок), представленный преимущественно глинистыми и песчаными породами, а также чередованием песков, глин, алевролитов, аргиллитов, песчаников.

Коллектор залегает в интервале глубин 600-730 м и средняя толщина газонасыщенной залежи составляет 110 м. На этом основании составляем таблицу 1.

Падение пластового давления Р1-Р2=ΔР для расчета примем равным 2,5МПа, так как на ЗападноСибирских месторождениях с отработкой до 10 лет более высокие величины падения встречаются очень редко. Параметр упрочнения коллектора χ≈150.

За первоначальные элементы геологического разреза примем «базовые» значения физико-механических свойств пород, взятые из справочной литературы (табл. 1). При таких «базовых» значениях поле оседания горного массива будет направлено вниз по всей поверхности кровли сеномана в расчетном блоке, что подтверждается границами оседания грунта на дневной поверхности геодезическими фото материалами спутниковых радионавигационных систем [2, 5].

При этом согласно данных прогноза оседаний земной поверхности, полученных экспериментально [3, 4] на ряде нефтяных месторождений Западной Сибири, средние величины оседания дневной поверхности колеблются от 120 до 360 мм, при падении давления на 3 МПа и мощности коллекторов 35-55 м.

Однако практика показывает, что впервые годы добычи сырья (при извлечении его из пласта-коллектора до 10% от общего объема и снижении пластового давления до 20% от начального), деформации происходят только в верхней части коллектора от 2% до 15% его толщины. Далее, при снижении пластового давления на 1/3 от начального, деформация охватывает объем до 30% толщины коллектора. Физически это можно объяснить тем, что эта часть коллектора, потеряв пластовое давление, сдерживает нагрузку своей пористостью и скелетом породы. Такой факт частично подтверждается работами Кузьмина Ю.О. и Жукова В.С. [4], и позволяет нам аппроксимировать величину оседания поверхности через расчет толщины деформированной зоны коллектора по изменению электрического сопротивления его пород и показателю падения пластового давления. Для упрощения расчета просадки толщину деформируемой зоны коллектора в средней стадии разработки (до 12 лет) можно принять равной 30%.

В нашем случае средняя мощность коллектора составляет 110 м, добыча ведется чуть более 10 лет, а значит, зона деформации верхней части не превысит 35 м. При потере давления на 25 атмосфер осадка мо-

Ah I h жет составить C = ;

Δσ где См – коэффициент одномерного уплотнения; hс – деформированная зона; h – толщина коллектора; ∆σ – изменение реакции скелета грунта, зависящая от потери давления в пласте.

Предварительный расчет величины осадок.

Расчет для случая одномерного сжатия применяется при большой площади загрузки, превышающей мощность сжимаемости слоя грунта в несколько раз. Боковое расширение грунта, срезающие усилия по периферии мульды не учитываются, а величина нормальных напряженностей (осевая нагрузка) принимается постоянной по всей мощности сжимаемого слоя.

aP

σ = h aP = ha P (2)

1 - n о где h – мощность сжимаемого слоя, n0 – начальное значение коэффициента пористости, a0 – коэффициент сжимаемости,

P – давление обусловленное пластами земной породы мощностью Н, рассчитывалось по формуле:

P = 5 • g • H = 9,8 • 5 • H (3)

где, δ – среднее значение объемного веса породы коллектора (0,02 МН/м3);

H – мощность сжимающей толщи пород до кровли исследуемого пласта (621 м)

P = 9,8∙0,02 ∙ 621=122 МН/м2 ;

Рассматриваемое давление уравновешивалось давлением газа (жидкости) в поровом пространстве Р г и реакцией пласта (силы упругости), сжатого продуктивного пласта σ z

Р= Р г + σ z    (4)

В результате извлечения газа его пластовое давление уменьшается, это уменьшение восполняется увеличением силы упругости и соответственно дополнительной деформации сжимаемого пласта. При этом сжимающее давление остается неизменным. Из этих соображений запишем

Δ Р г = Δ σ z    (5)

В этом случае для описания напряженно-деформированного состояния достаточно двух констант материала: модуля упругости Е и коэффициента Пуассона v. В соответствии с законом Гука напряжения и деформации в произвольной декартовой системе координат (х, у, z) можно связать между собой следующим соотношением (1):

• ^z ="---E^Iv^x + v£y +(1 - vК ];

• 1    - v - 2 v

Полагается, что свойства пород в плоскости залегания изотропными, тогда ε х = ε у и уравнение (1) примет вид:

E

^z =;------[TvVx-v^x + (1 -v)^z] (6)

• 1    - v - 2 v

Для предварительных расчетов пренебрежем членом 2 v ε х так как сжимаемый пласт испытывает боковое давление соседних пластов. Учитывая соотношение Δ Р г = Δ σ z и (6) выразим проседание породы над месторождением в результате извлечения газа в виде:

M        ,    AP, (1 -v - 2v2),

∆L = ∆ε ⋅ h = г            h (7)

z c       Е (1 -v)      c hc – толщина зоны деформации составляет 35., ∆P – величина изменения пластового давления (примерно равно 25 атм или 2,5 МПа на декабрь 2010 года). Если исходить из табличного значения модуля упругости Е=3,5·109 Па и hc=35, то абсолютная величина просе- дания составит

∆ L == ^{(1 -} ν ^{- 2} ν ^{2 )} ⋅ h ⋅ ∆ P = 0,21 ⋅ 10 ^{- 9} ⋅ 35 ⋅ 25 ⋅ 10⁶ = 0.184 м

E ⋅ (1 -ν)    c

Для более точного определения величины ΔL необходимо знать усредненный модуль упругости по пласту в предположении, что он деформируется упруго и не происходит слом скелета.

Полученное значение можно привести к просадке на единицу потери давления:

∆ ε = ΔL / ∆P) = 184:25=7.4 мм/атм.

На 01 .0 1 .201 3 г. величина изменения давления в коллекторе составила в среднем 30 атмосфер или 3,0 МПа. Тогда полная осадка за 13 лет верхней части коллектора составит 184 мм, а просадка будет равной 6,13 мм/атм.

Вывод. Полученная величина показывает, что напряжение в коллекторе прямолинейно нарастает, и процесс деформации проходит за счет снижения пористости между частицами, т.е. без разрушения скелета горных пород. Эта величина может служить фоновым показателем для последующих расчетов, анализа и построения мульды оседания дневной поверхности любого месторождения по косвенным критериям на базе прямых и дистанционных измерений параметров разработки продуктивного пласта.