Построение мультисервисных сетей на основе функциональных преобразований трафика

Основу конкурентоспособности сетей связи составляет стабильное качество обслуживания пользователей. Под качеством услуг связи понимается суммарный эффект от параметров обслуживания, который определяет степень удовлетворения пользователей услугами связи (рекомендация Е.800 МСЭ). В связи с созданием сетей нового поколения (NGN) на первое место выходит принцип отделения функций образования служб/услуг от транспортных функций. По сути, речь идет об интегрированных мультисер-висных широкополосных услугах и методологий предоставления гарантированного качества услуг (SLA). Здесь под широкополосностью понимается возможность гибкого и динамического изменения скорости передачи информации в широком диапазоне в зависимости от текущих потребностей пользователя, а мультисервисность означает независимость технологий предоставления услуг от транспортных технологий. Все сказанное относятся не к сети, а к службе, сеть же может обеспечить только услугу транспортировки сообщений.

Мультисервисная сеть (МСС) – это инфраструктура, использующая единый канал для передачи данных разных типов трафика. Она позволяет уменьшить разнообразие типов оборудования, применять единые стандарты и единую кабельную систему, централизованно управлять коммуникационной средой для предоставления наиболее полного спектра услуг.

Постановка задачи

На основании вышеизложенного сформулируем ряд требований, которым должна отвечать идеальная МСС. Такая сеть должна:

• -    эффективно использовать сетевые ресурсы;

• -    обеспечивать высокое качество обслуживания мультимедийного трафика;

• -    быть инвариантной к структуре трафика.

Наиболее полно такая сеть может быть реализована на основе использования системы массового обслуживания (СМО) общего вида M/M/n/m. Эта модель СМО достаточно хорошо разработана и позволяет решить задачу эффективного ис- пользования сетевых ресурсов в конечном виде. Кроме того, она позволяет оценить основные качественные показатели сети, такие как минимальное среднее время задержки сообщений и вероятность отказа в их обслуживании. Однако данная модель изначально предназначена для обработки пуассоновских потоков информации с экспоненциальным временем обслуживания.

Для того чтобы данная модель СМО полностью удовлетворяла изложенным выше требованиям, в основу создания инвариантной системы к различным структурам трафика может быть использован метод функциональных преобразований, основанный на свойствах инвариантности формы дифференциала вероятности и независимости переменных [1]. Данный метод позволяет адаптировать произвольный входной трафик к пуассоновской модели сети связи. Таким образом, требуется решить задачу инвариантности МСС к структуре входного трафика на основе его функциональных преобразований в узлах коммутации и представления сети СМО наиболее общего вида M / M / n / m .

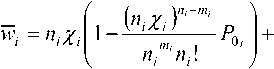
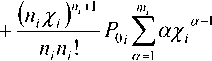
Вероятность отказа в обслуживании, когда все каналы и места в очереди заняты, согласно [2-3], равна

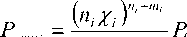
отм            _т- ^uz

ПР.!^ '

Выразим P_Qj из (4) и получим

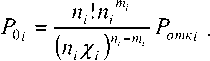
Зафиксируем вероятность отказа на некотором допустимом уровне

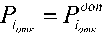
и, подставив (5) в (3), получим среднее число заявок в СМО:

Модель экспоненциальной сети

Каждое i -ое звено транспортной сети моделируется в виде СМО типа M / M / n / m [2] с ограниченной очередью ( n -канальная СМО с ожиданием), на которую поступает пуассоновский поток заявок с интенсивностью Я_;, интенсивностью обслуживания //, и числом мест в очереди для i -го звена m_i . Среднее число занятых каналов z_i и среднее число заявок, находящихся в очереди r_i для каждого звена сети определяются уравнениями [2]:

w, ^{= n}iXi^^_p_omK,)+ ^p_omK^“Xi ^    (7)

z z \ отк i / отк z / z            ^.

a=A

Такая подстановка позволила упростить функционал оптимизации. На основании формулы Литтла и с учетом гипотезы Клейнрока о независимости запишем [2]:

X^aO^'Lwi:

Z=1

^, =аО-

( \п+т

«X)

ni -п'

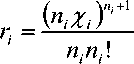
рА«хГх

где: Pi – степень загрузки канала i -го звена; Xi = Pj ™i – эффективность использования канала; P _0i – вероятность того, что каналы i -го звена свободны. Для всей сети вероятность того, что каналы свободны, равна [2]:

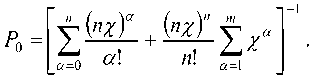
Среднее число заявок w_t в в звене СМО определяется суммой выражений (1) и (2) на входе в каждый канал СМО [2]

где / – общий трафик сети, T зад – средняя задержка пакетов.

Условие (7) с учетом допущения (6) позволяет определить такой важный качественный показатель сети, как среднее время задержки пакетов:

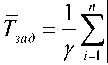
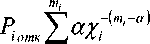
^ ^iXi(^ ^„„k) . (8)

1    ‘ ' 1отк '

a=l

В силу сепарабельности функции (8) запишем [2]:

8Т_{зад =} d_{Wi = Q} .                      (9)

8Xi dxs

Вычисление производных (9) приводит к сиc-

теме n уравнений вида:

'^_lm_i -a)»^,^-^^-^^-1^

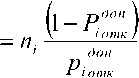
Однако по условиям задачи приемлемыми значениями являются только те, которые расположены на поверхности, определяемой уравнением [2]

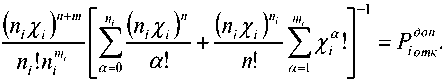
Преобразуем (10) и приведем его к виду i+±n™,-«W"H"*,l,=c:. (11)

/   \ z / /VI                 1отк zz, „ ।

Учитывая, что правые части выражений (10) и (11) равны, получим:

a\

a(m, —a) _ ^^ . (12) ⁿiZi

Уравнение (12) справедливо для любого звена изотропной сети, в которой z не зависит от направления передачи, то есть[2]:

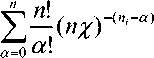
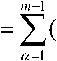
aim - a) ^Z

-W . (13)

Определим корни уравнения (13), изменяющиеся в пределах OX np . Исследования показали, что получить точное аналитическое решение (13) не представляется возможным ввиду его трансцендентности, но они могут быть решены численными методами. Численный метод решения реализован с помощью программы Mathcad. Определены зависимости оптимальных значений T зад и ^отк от сочетаний числа каналов n и количества мест в буфере m. Определив значения Xi np и величину суммарного потока на входе i-го звена (заданного матрицей нагрузок на линии связи сети ограниченной связности произвольной топологии – см., например, в [4]), можно найти необходимое число каналов передачи i-го звена и их пропускную способность, исходя из соотношения:

Z i _np ~ ^— г ^— p ’ (14) ^p n_f • jUj n, p.j r,. • п_;

ZZ =^^ = /(n,m). • zz.

Преобразование произвольного закона распределения интервалов времени между пакетами в пуассоновский закон

Пусть непрерывная случайная величина r, с плотностью распределения / (ri) подвергается функциональному преобразованию r2 = ^(r,) . Поскольку при этих условиях выполняется свойство инвариантности дифференциала вероятности, то вероятности этих двух событий равны [1]

g(4W^_ ^/(^idT, .         (15)

Необходимо выбрать такую функцию Ф ’ которая в результате преобразования позволила бы получить экспоненциальный закон распределения g(r₂) = Яехр(-Яг₂), где r₂ – длительность интервала времени между пакетами. Функция распределения при этом согласно [1] равнаС(г₂) = 1-е"^Лг2. На основании свойства (15) получим

d T f^^ = g{Ta^- Тз атл

-|ln[l-F(r,)]

Структурная схема устройства для преобразования входного трафика показана на рис. 1. Устройство содержит входную шину 1; логические элементы «И» 2-3 и 9-10; счетный триггер счетчики 4-5; выходной элемент «ИЛИ» 6; элементы буферной памяти 7-8; выходную шину 11 и вычислительное устройство 12.

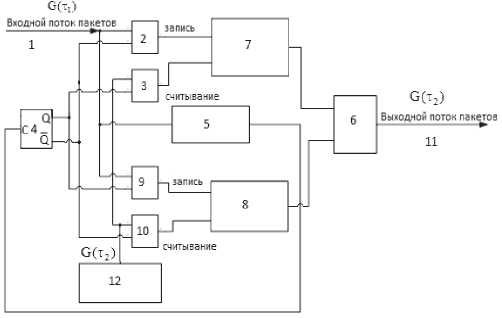
Рис. 1. Преобразование потока пакетов G(r,) в поток Gkji)

Пример

Покажем возможность преобразования входного потока пакетов G(?"i), имеющего плотность распределения интервалов времени между пакетами по закону Парето, в пуассоновский поток, используя подход, реализованный в устройстве рис. 1. Предполагается, что преобразование трафика носит циклический характер, эффективность процесса преобразования определяется степенью точности стыковки элементов циклов между собой.

Длительность каждого цикла /" определяется временем накопления фиксированного числа пакетов m_x в счетчике 5. Поскольку закон преобразования трафика имеет случайный характер, получим:

"'1(7+1)

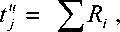
mJ

где R, – последовательность пакетов, интервалы времени между которыми полностью определяют статистические свойства входного трафика ^(^ri) • Эта последовательность приведена на рис. 2 для распределения интервалов времени между пакетами по закону Парето, при = 100. Она формируется с помощью специальной программы, как выборка случайных величин с распределением интервалов времени между пакетами по закону Парето, обладающего заведомо самоподобными свойствами, интегральная функция распределения которого имеет вид[1]:

^) = 1-

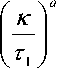
ность циклов записи процесса ^(ri), построенных по формуле (16), приведена рис. 3.

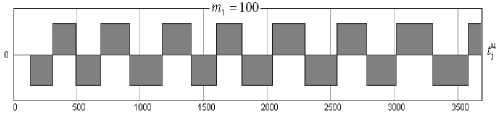
Рис. 3. Длительность циклов, записанных в элементах буферной памяти емкостью m, = 10 ²

В отрицательной области рис. 3 показан процесс записи в элемент буферной памяти 7, а в положительной области – в элемент буферной памяти 8 рис. 1. На рис.3 показано 15 полных циклов записи процесса GC^) . Считывание из элементов буферной памяти осуществляется аналогично, но в качестве управляющей последовательности используется последовательность пакетов ^(2"? ) ? формируемая вычислительным устройством 12 рис. 1. При использовании данного устройства в экспоненциальных сетях предполагается применение пуассоновского закона, имеющего экспоненциальное распределение интервалов времени между пакетами F(r^) = 1 — exp(2r₂), где A – управляемая интенсивность потока пакетов.

Генерируемая вычислительным устройством 12 (см. рис. 1) последовательность пакетов G^Ji) представлена на рис. 4, интервалы времени между пакетами равны t^ =—-ln(l-rnd(l)^. (18)

где к – нижний граничный параметр, а – коэффициент формы.

Рис.2. Входная последовательность пакетов G(ri)

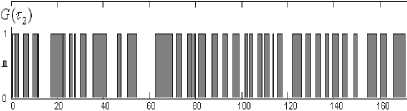
180        200

Рис. 4. Последовательность пакетов G^t^ )

Для генерирования случайных величин с распределением Парето необходимо найти обратную функцию от интегральной функции распределения [1]

При этом длительность циклов (см. рис. 5) по-прежнему описывается формулой (16), в которой интервалы времени между пакетами равны R, =T"₂.

к

(l — rnd(A^7<

где rnd (1) – случайная переменная, равномерно распределенная на интервале [0; 1]. В последовательности рис. 2 пакеты располагаются во всех точках опрокидывания процесса R; . Длитель-

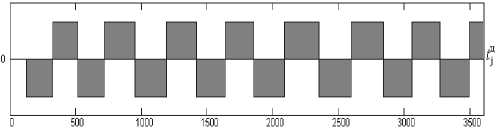
Рис. 5. Длительность циклов, считываемых из элементов буферной памяти

Связь между параметрами а (входной трафик, закон Парето) и я (выходной трафик, пуассоновский закон) в (17)-(18) показана на рис. 6.

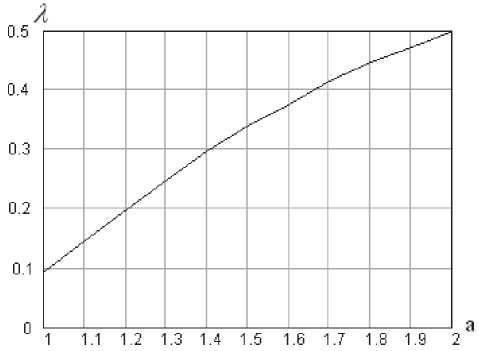
Рис. 6. Связь между параметрами я и Л

Параметры процессов, формируемые в устройстве преобразования трафика, соответственно для закона Парето и экспоненциального закона, приведены ниже. Формирование потоков пакетов G(ri) – см. рис. 2 и С/^7~2 ) – см. рис. 4 соответствует

^) =

R(r2) =

М --—— , я = 0,7;

tj <- — ln(l -Nf ,X = 0,37534;

X t.

Объединение потока пакетов Cr^) – см. рис. 3 и Gf^) – см. рис. 5 в циклы, содержащие 102 пакетов, соответствует fori e 0...99;

ю^ап

Г, а £л(г,), ;

/=100,

T, fori g 0...99;

100|;+ll f^ ^Rf2\;

/=1 00,

T.

Определение математического ожидания потока пакетов G(ri) рис. 3 и G(t"₂) рис. 5:

£д.(г,)

^MtT''^{) = y}f^ --^; W,) = 269,743;

S£x^)

W2)="°99  ; M(r2) = 269,743.

Определение дисперсии потока пакетов ^(^i) рис. 3 и Gf₇ ) рис. 5:

^fGd-Mff1

Df_x^^ -------------; D(r,) = 6,317-10³;

^fff-Mffy

Df,) = ----- —-------; D(t₂ ) = 943,063.

Определение джиттера задержки потока пакетов Gf^ рис. 3 и Gf₂ ) рис. 5:

Z>(r,) = 79,48; Df₂} = 30,71.

Протяженность процессов различных по своей природе удалось сопоставить между собой по величине математического ожидания. Здесь основным управляющим показателем является интенсивность X пуассоновского закона, сопоставляемого с коэффициентом формы а закона Парето.

Джиттер задержки характеризует степень отличия исследуемых процессов в моменты переполнения счетчика 5 рис. 1 и может составлять 10 …15% в сравнении с математическим ожиданием, он характеризует качество функционирования предлагаемого устройства.

Заключение

В статье предложена структурная схема рис. 1, позволяющая достигнуть инвариантности входного трафика за счет использования функциональных преобразований и свойств экспоненциальных сетей, в которых в качестве модели информационного обмена используется СМО M/M/n/m. Для данной СМО получены аналитические зависимости, позволяющие оптимизировать среднюю задержку, вероятность отказа в обслуживании пакетов в зависимости от числа каналов и количества мест в буферной памяти, а также выбрать оптимальные приемлемые коэффициенты загрузки каналов, характеризующие эффективность функционирования сети. Муль- тисервисная сеть может быть реализована на основе использования в качестве модели системы массового обслуживания наиболее общего вида M/M/n/m с последующими функциональными преобразованиями входного трафика в пуассоновский закон. Такой подход дает возможность решить задачу обработки произвольного трафика экспоненциальной сетью, делая ее инвариантной к структуре входного трафика.