Построение нечётких регуляторов для систем управления автономных объектов в среде SimInTech

Стадия проектирования является определяющей в жизненном цикле изделий штучного и мелкосерийного производства. Использование интегрированных систем проектирования технических устройств позволяет повысить их качество и сократить сроки разработки.

Одним из перспективных средств моделирования и разработки робототехнических и других сложных систем является среда визуального моделирования SimInTech [1; 2; 7 – 9], которая обеспечивает:

• •    создание моделей технических устройств в виде структурных блок-схем;

• •    математическое моделирование их режимов на основе дифференциальных уравнений;

• •    создание составных моделей технических объектов из готовых блоков – моделей оборудования;

• •    интеграцию в единую комплексную модель;

• •    отладку алгоритмов управления на модели и реальном объекте;

• •    автоматическую генерацию кода управляющих программ;

• •    автоматизацию выпуска конструкторской документации.

Одной из основных особенностей использования SimInTech для создания комплексных моделей является идеология использования «Базы данных сигналов» – структурированного списка переменных, обеспечивающих обмен расчётными значениями между расчётными схемами в единой модели. База данных сигналов SimInTech является объектной и обеспечивает пользователю удобное решение следующих задач:

• •    объединение нескольких расчётных схем в единую модель;

• •    обеспечение возможности векторной обработки сигналов для типовых алгоритмов управления;

• •    объектно-ориентированное проектирование модели технических систем;

• •    автоматизация создания и обработки переменных в комплексных моделях.

Для создания сложной математической модели происходит объединение моделей основных подсистем, реализованных в виде отдельных проектов, в единый пакет. В настоящее время пакет SimInTech используется на ряде предприятий ракетно-космической техники.

Во многих отраслях промышленности в отношении технических систем, характеристики которых в процессе работы могут изменяться в широком диапазоне, применяют алгоритм нечёткой логики [3; 4; 6].

Некоторые задачи, выполняемые искусственными спутниками Земли (ИСЗ), могут потребовать постоянного определения его местонахождения относительно Земли. В этом случае ИСЗ в любой момент полёта по орбите должен определять свои географические координаты и высоту над поверхностью Земли.

Эта задача является весьма сложной, и ее решение будет одним из основных факторов, отличающих автоматизированный ИСЗ от неавтоматизированного. Наиболее совершенными будут стабилизированные автоматизированные ИСЗ, которые должны занимать строго определенное, известное положение в пространстве [10; 11].

Стабилизация угловых положений ИСЗ на орбите необходима, во-первых, для удержания поверхности солнечной батареи в направлении на Солнце и, во-вторых, для придания определённого положения ИСЗ относительно Земли с целью автоматического фотографирования определённых участков земной поверхности, более надёжной связи с Землей, наблюдения за движением льдов, масс облаков, спасения кассет с результатами научных наблюдений и т. д.

Рассмотрим процесс построения нечёткого регулятора в среде SimInTech на примере системы управления угловым положением искусственного спутника Земли.

Постановка задачи

По заданной математической модели автономного объекта необходимо реализовать в среде SimInTech управление аналоговым, дискретным и нечётким регулятором. Также необходимо осуществить реализацию регуляторов и произвести настройку их параметров, и, затем, сравнить полученные результаты.

Динамическая модель объекта

Функциональная схема и исходные данные автономного объекта представлены в [5]. В качестве примера рассмотрим систему управления угловым положением ИСЗ (рис. 1).

Создадим динамическую модель (рис. 2) в среде структурного моделирования SimInTech функциональной схемы (рис. 1) по уравнениям её элементов [2].

Передаточная функция аналогового корректирующего устройства (КУ):

W = u3 = ky • p .

u 2 Ty • p + 1

Передаточная функция маховичного исполнительного органа по напряжению:

M v( P )

W, = ф ⁽ p )

^кИО ' koc ' p _ ³⁰ p

ТИО • P + 1   5 P + 1

Передаточная функция корпуса ИСЗ:

Тисз • p2   1000 • p2

Здесь k = 2, k_u = 10, k_m = 0,5 – коэффициенты усилителя корректирующего устройства, усилителя напряжения и усилителя мощности соответственно.

Применяя блок оптимизации, проведём настройку параметров аналогового регулятора в плоскости его параметров k_ky и T_ky .

Кривая регулирования аналогового инерци-онно-дифференцирующего КУ представлена на рис. 6 под цифрой 1.

Статическая ошибка регулирования составляет 10 %. Дальнейшее уменьшение ошибки за счёт увеличения коэффициента k_ky невозможно, т. к. существенно снижается запас устойчивости системы.

Построение регуляторов

Для повышения точности ориентации объекта включим на вход системы дискретный ПИД-регулятор (рис. 3).

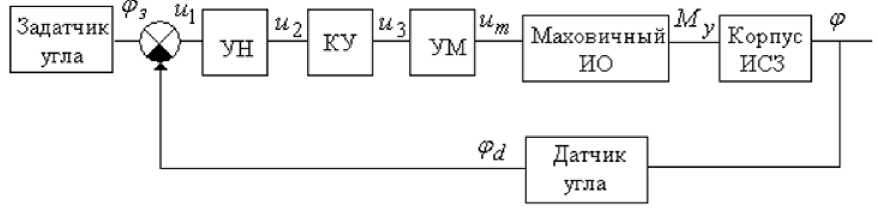
Рис. 1. Функциональная схема системы управления угловым положением искусственного спутника Земли [5]

Блок дискретного ПИД-регулятора представляет из себя субмодель, в которой используется стандартный блок «Дискретный ПИД-регулятор». Период квантования задан равным 0,001 и использован стандартный блок оптимизации среды SimInTech.

Параметры регулятора K_p , K_i , K_d

про-

порциональная, интегральная и дифференциальная составляющие соответственно – задаются в виде глобальных переменных и вносятся в блок «Сигналы». Для настройки регулятора используется блок «Оптимизация». В качестве метода оптимизации применяется симплекс-метод.

В результате оптимизации вектор из трёх коэффициентов (составляющих) направляется в блок «Запись в список сигналов», откуда вычисленные значения перенаправляются в дискретный ПИД-регулятор, изменяя его параметры. В блоке

Том 3

«Оптимизация» заданы следующие свойства: абсолютная точность подбора значений выходов – 0,01, начальное приближение выходов блока – 1, минимальное значение выходов блока – 0.

В рассматриваемом случае блок оптимизации рассчитал следующие оптимальные значения коэффициентов: K_p – 1,5, K_i – 0,1, K_d – 4,5.

Результаты моделирования представлены на рис. 6 под цифрой 2.

Далее реализуем регулятор на базе нечёткой логики [3; 6].

Для начала выполним фазификацию входной переменной. Наш блок будет получать на вход одно значение и оценивать его, насколько данная величина соответсвует заданным в параметрах термам. Мы будем расчленять исходную величину на несколько термов, рассчитывая для каждого терма функцию принадлежности µ( x ) типа кривой Гаусса.

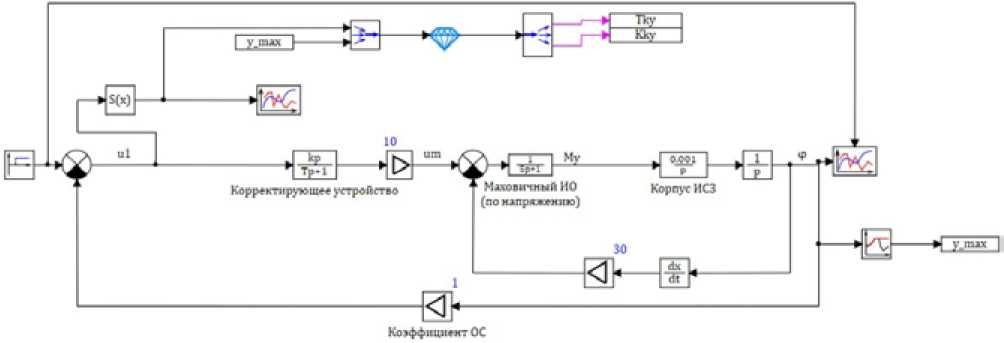
Рис. 2. Динамическая модель системы, реализованная в проекте SimInTech

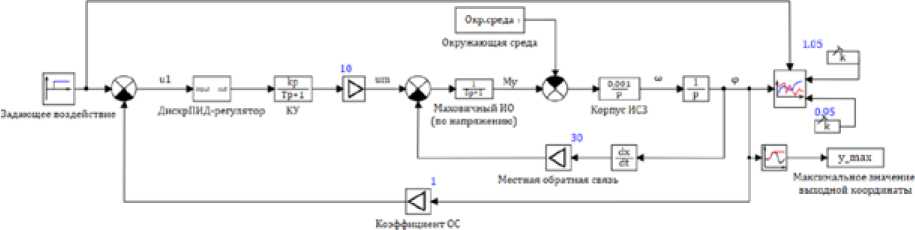
Рис. 3. Динамическая модель системы управления угловым положением ИСЗ с применением дискретного ПИД-регулятора

В базе правил нечёткой логики будем использовать следующие терма:

• 1.    Для отклонения: меньше нормы, норма, больше нормы.

• 2.    Для скорости: увеличивается, не изменяется, падает.

• 3.    Для ускорения: ускоряется, не изменяется, замедляется.

Выход тоже будет иметь три лингвистические переменные: «уменьшать», «не изменять», «увеличивать».

Сформулируем правила нечёткого регулирования для управления угловым положением объекта и опишем их в виде лингвистических выражений:

• 1.    Если больше нормы и отклонение растёт, а скорость роста увеличивается, то уменьшаем.

• 2.    Если норма и отклонение не изменяется, а скорость постоянна, то не изменяем.

• 3.    Если меньше нормы и отклонение падает, а скорость падения увеличивается, то увеличиваем.

Для удобства зададим следующие параметры в глобальные переменные и оптимизи-

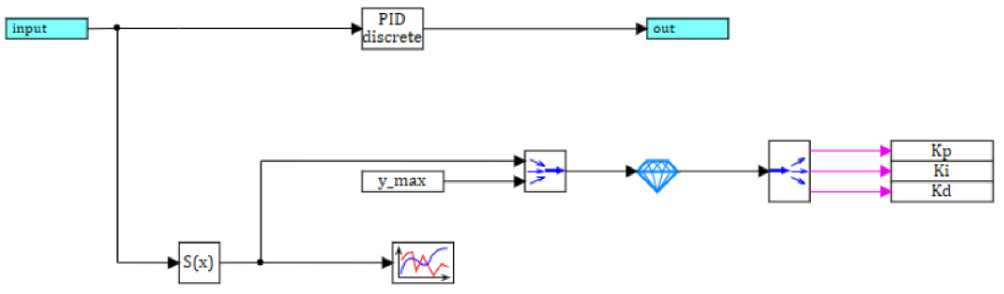
Рис. 4. Содержимое субмодели дискретного регулятора

Коои'*естви перёклямемий

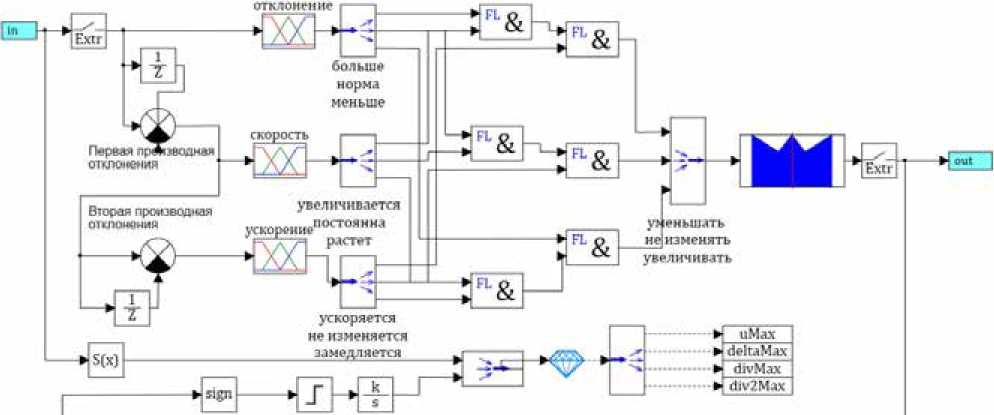
Рис. 5. Содержимое субмодели нечёткого регулятора

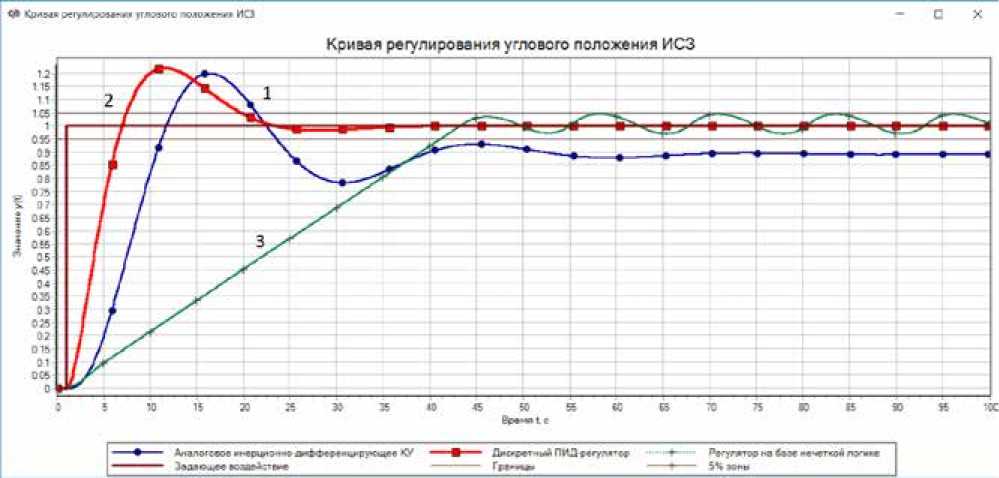
Рис. 6. Результаты моделирования системы с применением регуляторов различного типа

руем их при помощи блока оптимизации среды SimInTech:

• 1.    uMax – амплитуда управляющего воздей-

• ствия;

• 2.    deltaMax – максимальное

• 3.    divMax – максимальная клонения;

• 4.    div2Max – максимальная дная отклонения.

  отклонение;

  производная от-

  
  

  вторая произво-

  
  

Заключение

На основе типовых блоков SimInTech построена и протестирована модель регулятора на основе нечёткой логики, проведена настройка па-

Том 3

раметров модели при помощи блока оптимизации среды SimInTech.

Выполнено моделирование системы управления угловым положением ИСЗ с использованием инерционно-дифференцирующего аналогового регулятора, дискретного ПИД-регулятора, а также регулятора на основе нечёткой логики.

Регулятор на базе нечёткой логики обеспечивает качество переходного процесса, сопоставимое с ПИД-регулятором, обеспечивая при этом большую гибкость в настройке, но требует настройки большего количества параметров.

Аналогично в среде SimInTech могут быть построены нечёткие регуляторы для управления другими автономными объектами.