Построение низкоэнергетической траектории перелета Земля – Луна – Земля с применением оптимизационных процедур

Подготовка экспедиций к Луне в настоящее время является одной из задач в космической отрасли [1; 2]. В зависимости от целей миссии реализуется одна из трёх программ: посадка на Луну, выход на орбиту вокруг Луны или облёт спутника. В случае реализации последней программы и необходимости возвращения космического аппарата (КА) на Землю встает вопрос о расчете параметров траектории, обеспечивающей достижение верхней границы атмосферы Земли на терминальном участке перелёта.

Для решения задачи формирования траектории полета КА существуют различные подходы. Метод построения траектории полёта, предлагаемый в работе [3], включает в себя аналитический расчет точек траектории и численное интегрирование уравнений динамики КА. При этом полученная схема полёта предполагает выполнение трёхимпульсной коррекции. В работе [4] построение траектории полёта выполняется на основе динамической модели движения КА с использованием эфемерид Земли, Луны и Солнца, рассчитанных заранее. При этом для получения непрерывной траектории полёта КА предполагается итеративное уточнение набора параметров движения.

В существующих методах решение рассматриваемой задачи реализуется за счет формирования и решения краевой задачи с использованием численного интегрирования дифференциальных уравнений, описывающих динамику КА с учётом гравитационного воздействия небесных тел. Однако, ввиду большого количества учитываемых параметров, объем времени, требуемый для получения решения, становится достаточно большим, поэтому в данной работе предлагает- ся формировать траекторию полёта КА с использованием комбинации приближенного аналитического метода и численного метода оптимизации. Подход к решению поставленной задачи, включающий в себя вычисление параметров орбит и вектора состояния КА, а также решение оптимизационной задачи, схематично представлен на рис. 1.

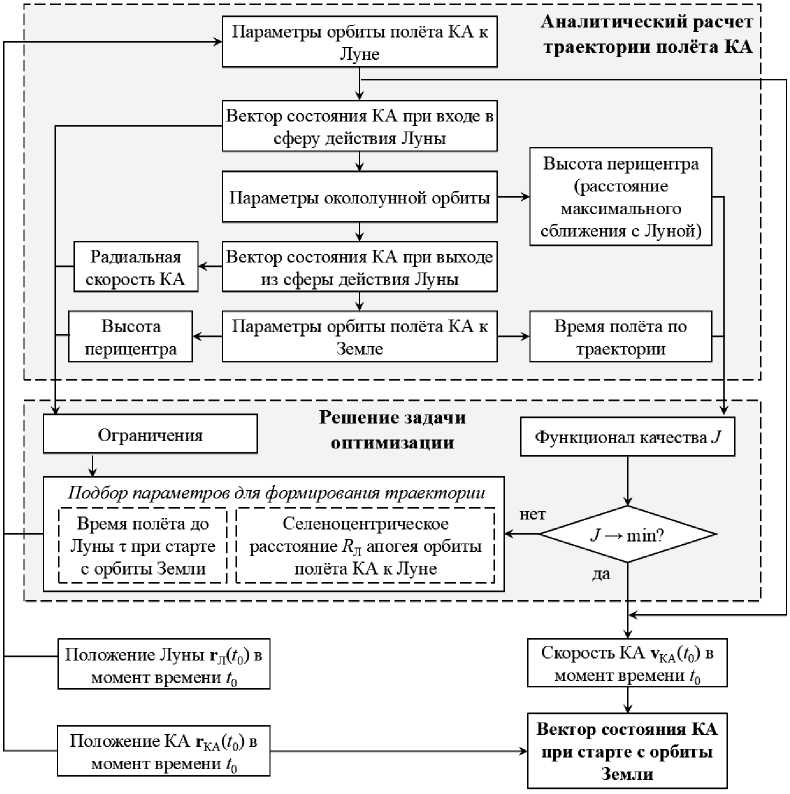
Рис. 1. Схема вычислений в предлагаемом подходе к формированию траектории полёта КА

Fig. 1. Calculation scheme in the proposed approach to forming the flight trajectory of a spacecraft

В общем случае рассматриваемая задача оптимизации является многоэкстремальной, поэтому целесообразно использовать эволюционные методы оптимизации, в частности, генетический алгоритм [5]. Генетический алгоритм активно применяется в решении оптимизационных задач авиационной и космической отраслей [6], например, для настройки контуров систем управления БПЛА [7] и стабилизации КА в режиме разгона двигателей маховиков [8], регулирования двухроторной аэродинамической системы [9], формирования программы тангажа в задаче выведения ракеты-носителя [10].

Построение схемы полёта КА

Построение орбит полёта выполняется методом сфер действия (рис. 2). Сначала определяется геоцентрическая траектория полёта к Луне, которая выводит КА из сферы действия Земли в сферу действия Луны. После этого выполняется расчет траектории полёта КА относительно Луны внутри указанной сферы. На последнем этапе определяется траектория ухода КА от Луны. Для обеспечения возвращения КА на Землю и достижения требуемой высоты перигея орбиты, по которой выполняется данный полёт, необходима импульсная корректировка траектории [11; 12].

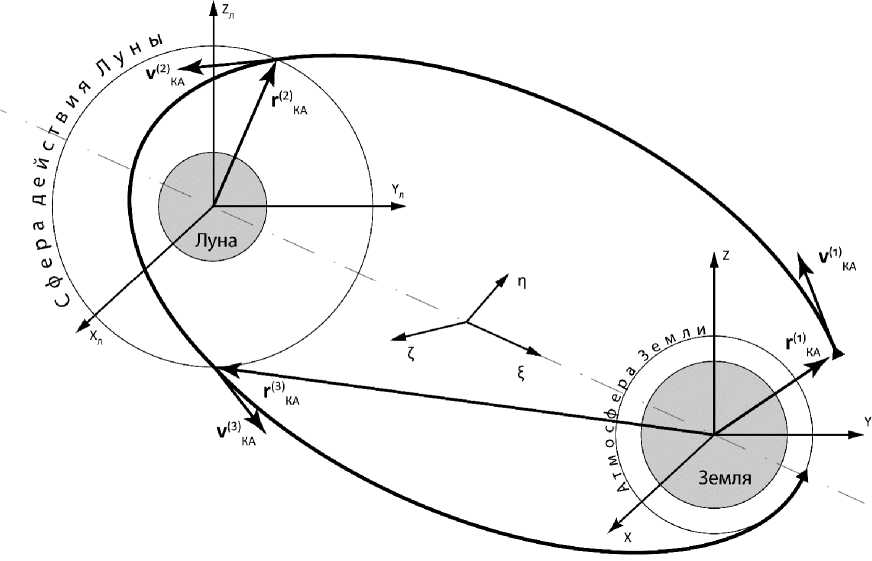
Рис. 2. Схема полёта КА

Fig. 2. Flight diagram of the spacecraft

С целью снижения энергетических затрат за выполнение перелёта Земля – Луна – Земля рассматривается пассивный полёт КА, при котором осуществляется единственный импульс скорости на орбите Земли после завершения этапа выведения. Следовательно, параметры каждого участка траектории КА, в том числе параметры орбиты, по которой выполняется полёт КА от Луны к Земле, определяются начальными условиями.

Траектория перелёта Земля – Луна – Земля делится на три участка, орбиты каждого из которых определяются в виде конических сечений [13]. Первый участок траектории представляет собой геоцентрическую орбиту полёта КА к Луне. На втором участке траектория соответствует полёту КА внутри сферы действия спутника по селеноцентрической орбите. Последний третий участок представляет собой траекторию ухода КА от Луны и возвращение на Землю по геоцентрической орбите. Далее в обозначениях, например в r _К ⁽¹ _А ⁾ , верхний индекс указывает на принадлежность параметра к k -й орбите (участку), где k = 1,2,3.

Рассмотрим первый участок перелёта Земля – Луна – Земля. Определяется геоцентрическим радиусом-вектором КА r _К ⁽¹ _А ⁾ в задаваемой точке старта, радиусом-вектором апогея первой орбиты г® и временем полёта до апогея т _{1 - г} (рис. 3). Апогей орбиты располагается на продолжении отрезка, соединяющего центры масс Земли и Луны в упрежденной точке:

r a ¹) = ^г л ⁽ t о +^т 1 - г ) + гЛ тт +Мл R л^{, (1)}

^Г Л⁽ t 0 ^+Т 1 - 1 ' )

где 1 0 - время старта КА, с; г _Л ( 1 0 + Т 1 — 1 . ) - геоцентрический радиус-вектор Луны в момент времени 1 0 + Т 1 — 1 . , км; R _Л - селеноцентрическое расстояние до апогея первой орбиты, км.

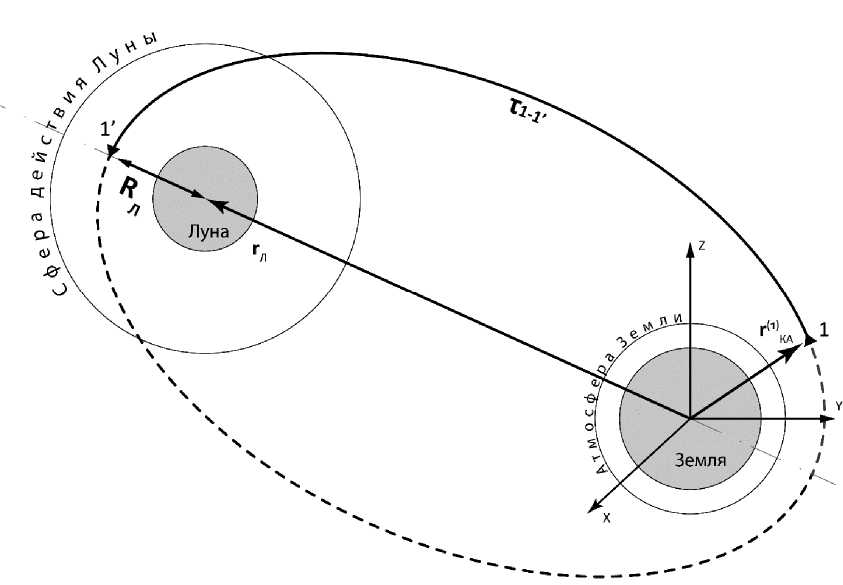
Рис. 3. Формирование орбиты полёта КА от Земли к Луне

Fig. 3. Formation of the orbit of the spacecraft flight from the Earth to the Moon

По рассчитанным гККА, г® и Т1_г затем определяются элементы первой орбиты полёта сле- дующим образом

{ e >", p '", S <“ ( 1 0 ), Я®, » '“ , , -'“ } = f ( e С V,.) ,

где e - эксцентриситет; p - фокальный параметр, км; 9 ( 1 ₀) - истинная аномалия КА в момент старта 1 ₀ , град.; Я - прямое восхождение, град.; О) - аргумент перицентра, град.; i - наклонение, град.; f ( • ) - условное обозначение процедуры вычисления указанных параметров, детальное описание которой приведено в работе [10]. Далее вычисляются истинная аномалия 3 ⁽¹’ ( t , ) КА и геоцентрический радиус-вектор до Луны г _Л( t , ) в момент времени t , вхождения КА в её сферу действия.

Рассмотрим второй участок перелёта Земля – Луна – Земля. Сначала определяются селеноцентрические радиус-вектор КА r _К ⁽² _А ⁾ и вектор скорости КА v ⁽ _К ² _А ⁾ :

{гКА’, vKA}= f (Гл(t,).e<",Р"’. 9"’(ti),«(u,О1),i’”)•(3)

(2)(2)

По рассчитанным rКА и vКА выполняется расчет параметров второго участка полёта – се- леноцентрической орбиты полёта КА при движении в сфере действия Луны:

{e“, p<2’, 9(2’(ti), Я(2’, .о , i(2’,r,(2’} = f (г®, v£),(4)

где r _n ⁽²⁾ - радиус перицентра орбиты, км. Затем определяются истинная аномалия Э ⁽²⁾ ( 1 ₂ ) КА и геоцентрический радиус-вектор Луны r _Л ( t ₂ ) в момент времени t ₂ выхода из сферы действия Луны.

Рассмотрим третий участок перелёта Земля – Луна – Земля. Сначала вычисляются геоцентрический радиус-вектор КА r _К ⁽³ _А ⁾ и вектор скорости КА v ⁽ _К ³ _А ⁾ :

{ rS . v KA } = f ( e A p A ■• ( 1 2 ), a¹", ®^m, i¹’ ) ■                    (5)

На основе полученных данных выполняется расчет параметров третьего участка полёта – геоцентрической орбиты полёта КА от Луны к Земле:

{ e », p <³>, » (>) ( 1 2 ) a* «.« i ®, r?, v ®( 1 2 ) 1 3 } = f ( r», v КА ) ,              (6)

где v _r ( t ₂ ) – радиальная скорость КА в точке выхода из сферы действия Луны, км/с; t ₃ – момент времени достижения перигея третьей орбиты, с.

После этого определяется общее время полёта КА в соответствии с выражением t - ~ tn -- tn .

перелёта 3     0 .

Формирование траектории с использованием оптимизационных процедур

Каждая орбита полёта КА характеризуется набором Кеплеровых элементов. Поскольку полёт КА осуществляется с использованием единственного импульса в начале перелёта, траектория полёта на втором и третьем участках определяется параметрами первой орбиты. При известной точке старта КА, для формирования первой орбиты требуется задание селеноцентрического расстояния R Л до апогея орбиты и времени полёта КА т _{1 - г} до указанной точки. Для построения схемы полёта вектор начальных значений задаётся в следующем виде:

x o =

R Л

^т 1 - 1 '

Таким образом, для рассматриваемой задачи формирования траектории полёта КА можно сформировать задачу оптимизации, которая заключается в подборе таких начальных условий, при которых расстояние максимального сближения КА с Луной и времени полёта по траектории является минимальным, т. е.

J = ^ а 1 w 1 ( r (²⁾ ) +а ₂ w ₂ A t² a min ,                         (9)

где Г (²⁾ — расстояние максимального сближения с Луной, км; a i - нормировочные коэффициенты; w _i – весовые коэффициенты.

Для подбираемого набора начальных параметров установлены верхние ( R max , т _{1 - Г} max ) и нижние ( R _min , T _{1 - fmin} ) границы области допустимых значений:

R min * R Л * R max

1 - 1 min      1 - 1       1 - 1 max

В оптимизационную задачу дополнительно вводятся нелинейные ограничения, которые позволяют учесть необходимость вхождения КА в сферу действия Луны, направление движения КА в точке выхода из указанной сферы, которое определяется знаком радиальной скорости, и достижение КА верхней границы атмосферы Земли. Эти условия можно записать следующим образом:

f ^{- 0}

- ( R 3 + * „■ ) - 0         ,                              (11)

|| ^ГКА ⁽ t 1 ) - ^ГЛ ⁽ t 1 ) 11 - ^R действ - ⁰

где v_r ⁽³⁾ – радиальная скорость КА в точке выхода из сферы действия Луны, км/с; r _π ⁽³⁾ – радиус перицентра третьей орбиты, км; R _З – экваториальный радиус Земли, км; h _атм – высота границы атмосферы, км; r _КА( t ₁) , r _Л( t ₁) – геоцентрические радиус-векторы КА и Луны в момент времени t ₁ вхождения в сферу действия Луны радиуса R _действ , км.

Для решения оптимизационной задачи используется генетический алгоритм. В качестве хромосом приняты селеноцентрическое расстояние R _Л до апоцентра первой орбиты и время полёта τ _{1 - 1 ′} КА до указанной точки при старте с орбиты Земли. Вектор, составленный из данных величин, образует особь. Набор особей формирует популяцию, участвующую в эволюции на каждой итерации генетического алгоритма. На рис. 4 представлено пространство решений функционала (9) с учётом ограничений (10) и (11). Видно, что решение оптимизационной задачи является сильно нелинейным.

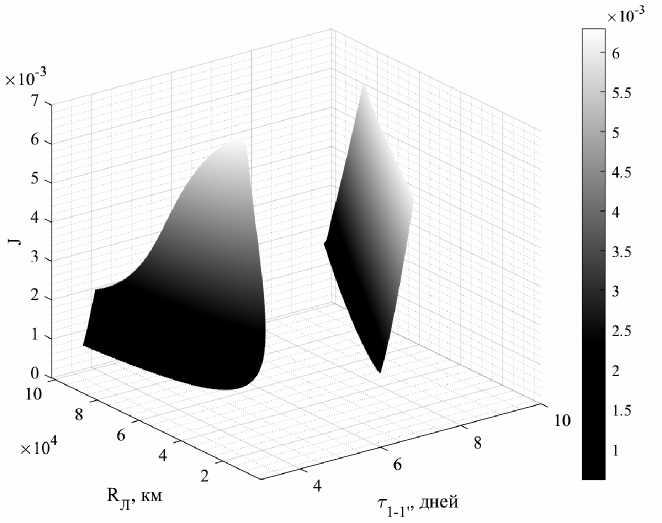
Рис. 4. Пространство решений задачи оптимизации

Fig. 4. Solution space of the optimization problem

Результаты расчета параметров траектории перелёта Земля – Луна – Земля

Для оценки корректности формирования траектории перелёта выполняется численное интегрирование дифференциальных уравнений, описывающих движение КА с учётом гравитационного воздействия Земли, Луны и Солнца. Для описания математической модели движения КА используется второй закон Ньютона, определяющий силу притяжения нескольких тел:

N

F КА =- Gm КА ∑ M i r ^КА r ⁱ ₃ ,                         (12)

i      rКА - ri где FКА – суммарная сила, действующая на КА, кг∙км/с2; mКА – масса КА, кг; Mi – масса i-го тела Солнечной системы, кг; rКА – радиус-вектор, определяющий положение КА, км; ri – радиус-вектор, определяющий положение i-го тела Солнечной системы, км; G – гравитационная постоянная, км3/ (кг∙с2). Для численного моделирования система приводится к нормальной форме Коши.

Параметры траектории полёта

Параметр	Значение
Селеноцентрическое расстояние R Л до апогея первой орбиты, км	60852,67531856347
Время полёта т 1_г до апогея первой орбиты, с	497861,4404235960
Элементы первой орбиты: – эксцентриситет e (1) –    фокальный параметр p (1) , км -    прямое восхождение Q (1) , град. -    аргумент перицентра ю (1) , град. –    склонение i (1) , град. -    истинная аномалия КА 9 ( 1 0 ) в момент старта 1 0 , град. -    истинная аномалия КА 9 (1)( t 1 ) в момент времени t 1 вхождения КА в сферу действия Луны, град.	0,970233718560075 12946,40576465826 7,801256161798105 27,963990027519067 27,517114189458532 0 178,7634087547173
Элементы второй орбиты: (2) – эксцентриситет e –    фокальный параметр p (2) , км -    прямое восхождение П (2), град. -    аргумент перицентра и (2), град. –    склонение i (2) , град. -    истинная аномалия КА 9 (2) ( t 1 ) в момент времени t 1 вхождения КА в сферу действия Луны, град. -    истинная аномалия КА 9 (2 ) ( 1 2 ) в момент времени 1 2 выхода КА из сферы действия Луны, град.	8,337589049815842 550659,8331189135 187,8012561617982 329,9971957197925 152,4828858105415 –25.971322612494077 25,971322612494077
Элементы третьей орбиты: – эксцентриситет e (3) –    фокальный параметр p (3) , км -    прямое восхождение Q (3), град. -    аргумент перицентра ю (3), град. –    склонение i (3) , град. -    истинная аномалия КА 9 (3) ( 1 2 ) в момент времени 1 2 выхода КА из сферы действия Луны, град.	0,971190044826021 12558,44980487381 7,801256161798059 26,575852741837750 27,517114189458436 181,5293711525792
Геоцентрический радиус-вектор КА r КА ( t 0) в точке старта, км		' 5379,14523655473 ' 3495,17652028344 _ 1423,57950818001 _
Вектор скорости КА v КА( t 0) в точке старта, км/с		'- 6.24160075029378 ' 7.78883694322032 4.46137142580742
Геоцентрический радиус-вектор Луны r Л( t 0) в точке старта, км		Г- 312078,982157000 ' 213237,985181000 _ 132125,221950000 _
Вектор скорости Луны v Л( t 0) в точке старта, км/с		Г- 0,581440000000000 - 0,707535000000000 _- 0,324062000000000		' ]

В таблице представлены искомые параметры R _Л и τ _{1 - 1 ′} , полученные в результате решения оптимизационной задачи, элементы орбит и вектора состояния КА и Луны в момент старта t ₀ . Размер начальной популяции особей генетического алгоритма принят равным 500.

На рис. 5–6 изображена траектория перелёта КА, состоящая из кривых, имеющих форму конических сечений. Параметры данной траектории были подобраны с использованием описанной процедуры с применением генетического алгоритма. Дополнительно представлена траектория, полученная при численном интегрировании дифференциальных уравнений с использованием тех же начальных условий. На графиках видно, что в каждой траектории обеспечивается облёт космическим аппаратом Луны и его дальнейшее возвращение в атмосферу Земли.

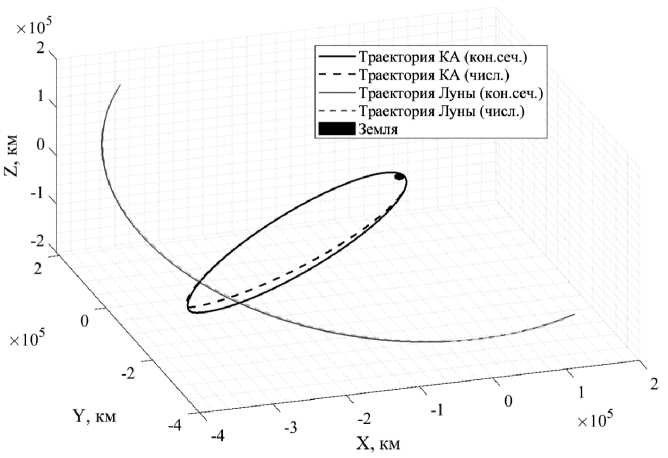
Рис. 5. Траектория перелёта КА в экваториальной системе координат

Fig. 5. Spacecraft flight trajectory in the equatorial coordinate system

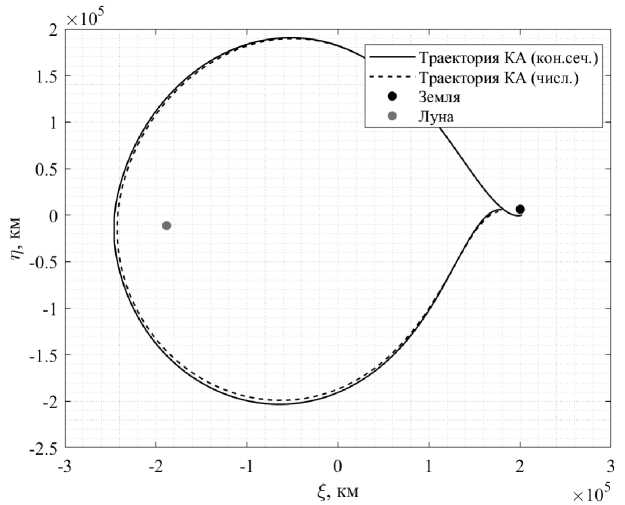
Рис. 6. Траектория перелёта КА в барицентрической системе координат

Fig. 6. Spacecraft flight trajectory in the barycentric coordinate system

Результаты, представленные в работе, подтверждают эффективность применения метода сфер действия в сочетании с оптимизационными процедурами при формировании траекторий типа Земля – Луна – Земля. Построенные схемы полёта КА показывают, что использование единственного импульса скорости на околоземной орбите является энергетически целесообразным решением, позволяющим обеспечить как облет Луны, так и последующее возвращение КА в атмосферу Земли.

Применение генетического алгоритма для решения задачи оптимизации позволило минимизировать как расстояние максимального сближения КА с Луной, так и общее время перелёта. Это демонстрирует целесообразность использования эволюционных методов оптимизации при решении задач небесной механики, характеризующихся выраженной нелинейностью и множеством локальных экстремумов [14].

Сравнительный анализ показал, что траектории, полученные методом конических сечений и с использованием численного интегрирования дифференциальных уравнений движения, практически совпадают. Данный результат свидетельствует о корректности предложенной методики формирования траекторий и подтверждает её применимость для предварительных расчетов миссий. Полученные результаты могут использоваться при предварительном проектировании миссий, аналогичных реализованным программам Apollo (NASA) или современным проектам возвращаемых миссий, обсуждаемым в рамках инициативы Artemis [15].

Заключение

В работе был выполнен расчет низкоэнергетической траектории перелета Земля – Луна – Земля с использованием комбинации метода сфер действия и генетического алгоритма. Траектория перелёта была поделена на три участка, каждый из которых представлял собой орбиту в виде конического сечения. Форма всей траектории определяется начальными условиями, в связи с этим для обеспечения облёта космическим аппаратом Луны и возвращения в атмосферу Земли необходима высокая точность при задании начальных параметров.

Для построения схемы полёта КА была сформулирована оптимизационная задача, которая численно решается с использованием генетического алгоритма. Был осуществлен подбор параметров, требуемых для формирования орбиты полёта КА к Луне при старте с орбиты Земли. Задача оптимизации сводилась к минимизации расстояния максимального сближения с Луной и времени полёта КА по траектории с учетом ограничений на условие вхождения КА в сферу действия Луны и условие, определяющее направление движения КА, что обеспечило облёт спутника и возвращение на Землю.

Было установлено, что варьирование весовых коэффициентов в функционале качества генетического алгоритма позволяет формировать различные траектории перелёта КА, в том числе и гравитационный маневр у Луны для полета к другим небесным объектам. Таким образом, можно сделать вывод, что использование оптимизационной задачи и генетического алгоритма как численного метода решения позволяет более эффективно рассчитывать траекторию полёта КА в лунных миссиях.