Построение оценок областей притяжения с помощью уравнений Ляпунова

Используя квадратичную функцию Ляпунова, докажем асимптотическую устойчивость нулевого положения равновесия системы [1, с. 228]

|    х = —у,

I у = X + (х² — 1)у.

Правая часть системы описывается вектор-функцией

"^(х,у) = ⁽ х + (х² — 1)у ^).

Матрица Якоби этой функции имеет вид [2, стр. 72]:

df _ /  0    —1

д(х,у) У¹ + 2 ^х у ^—1

А значит, матрица линейного приближения системы

А = агЦ (°'0)= (0 9(х,у)         V1

—1

—1

)

Значит, система первого приближения [1, с. 245] имеет вид

{ ^х = ^—у . (у = х — у

Функцию Ляпунова найдем в виде квадратичной формы с матрицей

L =

(^1    ^2\

V2    / а ).

При этом L - решение уравнения Ляпунова A^TL + LA

= —W , где ^ = (2

ATL

(—1

1 \ ^1  ^\   ( ^l2

— 17 V2   ^ 3/   \^—l1 ^—

A^TL + LA =

LA ₌ (^l1  ^l2\ 0  ^—1) ₌ (^l2

M₂  U⁽1  —1)   ⁽ l 3

( ^l 2           ^l 3 V (22 ^—l 1 ^{— l}2\

\ ^—l 1 ^{— l} 2    ^—l 2 ^{— l} 37   V3 ^—l 2 ^{— l} 37

(     ^2l 2         ^—l i ^{— l} 2 + ^l3\

Vk — l 2 + ^ 3    — 2(к + l3))"

^l 2

— l1 — l2— l2 — l3

(

—2 0

Получим систему линейных уравнений:

^l 3

— l2 — l3

—2

(   2l 2 = —2

< —l 1 — l₂ + l₃ = 0 , решение которой l 1 = 3, / 2 = —1, l₃ = 2.

(—2(l2 + l3) = —2

Следовательно, L =

(

—1

—1

) , а значит, функция Ляпунова для этой системы имеет

вид

V (%, у) = 3х2 — 2%у + 2у2.

Проверим положительную определенность матрицы L по критерию Сильвестра:

△ 1 =3>0; Д₂=| ³   —'|5>0,

—1  2

а значит, квадратичная форма V (%, у) положительно определена.

Значит, нулевое положение равновесия системы первого приближения асимптотически устойчиво.

• II.    Оценка области притяжения нулевого положения равновесия системы

Найдем производную V(%, у) в силу системы:

V(%,y) = (6% — 2у)%: + (—2% + 4у)у =

= (6% — 2у)(—у) + (—2% + 4у)(% + (%² — 1)у) =

= —6%у + 2у² — 2%² + 4%у — 2%у(%² — 1) + 4у²(%² — 1) =

= 2у² — 2%² — 2%у — 2%³у + 2%у + 4% 2 у² — 4у² =

= —2%² — 2у² — 2%³у + 4% 2 у².

Определим константу С из условия:

С= min V(%,y) =     min 2  (3%2 — 2%у + 2у2).

⁽ х,у ⁾ * ⁽ 0,0 ⁾               -2х³у+4х 2 у 2 =0

(х,у)*(0,0)

Получаем задачу условной минимизации:

( V(%,y) = 3%² — 2%у + 2у² ^ min

• —2%² — 2у² — 2%³у + 4% 2 у² = 0 .

%2 + у2 > 0

Попытка аналитического решения задачи приводит к системе нелинейных уравнений, которая не решается аналитически. Поэтому найдем решение этой задачи с помощью графического калькулятора Desmos .

В результате установлено приблизительное значение константы С ~ 4.6.

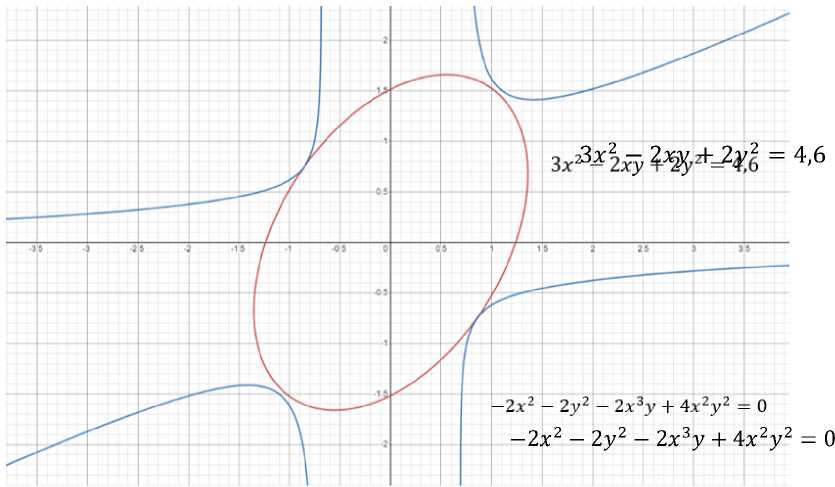
Рис. 1. Оценка области притяжения нулевого положения равновесия системы в графическом калькуляторе Desmos

Проведем вычислительный эксперимент, чтобы убедиться, что нулевое положение равновесия системы действительно имеет область притяжения, ограниченную уравнением 3x 2 — 2xy + 2у² = 4,6 .

Для этого выберем несколько начальных состояний, которые находятся внутри полученного эллипса , с шагом 0,5, за исключением начала координат. Все начальные состояния, которые были выбраны для вычислительного эксперимента, отражены в таблице 1.

Таблица 1. Координаты начальных точек, выбранных для вычислительного экспери- мента

№ точки	[хо ,У о ]	№ точки	[хо ,У о ]	№ точки	[хо ,У о ]	№ точки	[хо ,У о ]
1	[-1,0]	8	[0.5,0.5]	15	[0.5,1.5]	22	[-1,-1]
2	[-0.5,0]	9	[1,0.5]	16	[1,1.5]	23	[-0.5,-1]
3	[0.5,0]	10	[-0.5,1]	17	[-1,-0.5]	24	[0,-1]
4	[1,0]	11	[0,1]	18	[-0.5,-0.5]	25	[0.5,-1]
5	[-1,0.5]	12	[0.5,1]	19	[0,-0.5]	26	[-1,-1.5]
6	[-0.5,0.5]	13	[1,1]	20	[0.5,-0.5]	27	[-0.5,-1.5]
7	[0,0.5]	14	[0,1.5]	21	[1,-0.5]	28	[0,-1.5]

%initial conditions initmas = [-1 0;-0.5 0;0.5 0;1 0;-1 0.5; -0.5 0.5;...

0 0.5;0.5 0.5;1 0.5;...

• - 0.5 1;0 1;0.5 1;1 1;0 1.5; 0.5 1.5; 1 1.5;...

• - 1 -0.5; -0.5 -0.5; 0 -0.5;...

• 0 .5 -0.5;1 -0.5; -1 -1; -0.5 -1;0 -1; 0.5 -1; ...

• - 1 -1.5; -0.5 -1.5; 0 -1.5]';

%integrating t0 = 0; tf =15;

tspan = t0:0.05:tf;

Xmas = zeros(size(initmas,2),size(tspan,2));

Ymas = zeros(size(initmas,2),size(tspan,2));

for k = 1:size(initmas,2)

state0 = initmas(:,k);

[Tcom,Soltek] = ode45(@prstate, tspan, state0);

Xmas(k,:) = Soltek(:,1);

Ymas(k,:) = Soltek(:,2);

end

%plot figure for k = 1:size(initmas,2)

plot(Xmas(k,:), Ymas(k,:), 'black','LineWidth',1.5); hold on end ezplot('3*x.^2-2*x.*y+2*y.^2 - 4.6');

grid on axis equal axis([-2 2 -2 2]);

set(gcf,'Color','w');

set(gca,'Color','w');

set(gca,'FontSize',16);

function z = prstate(~, state)

%prstate computes the right side of the equation z = zeros(2,1);

z(1) = -state(2);

z(2) = state(1) + (state(1)^2 - 1)*state(2);

end

Рис. 2. Листинг программы в системе MATLAB

Фазовые траектории исходной системы при различных начальных состояниях изображены на рисунке 3.

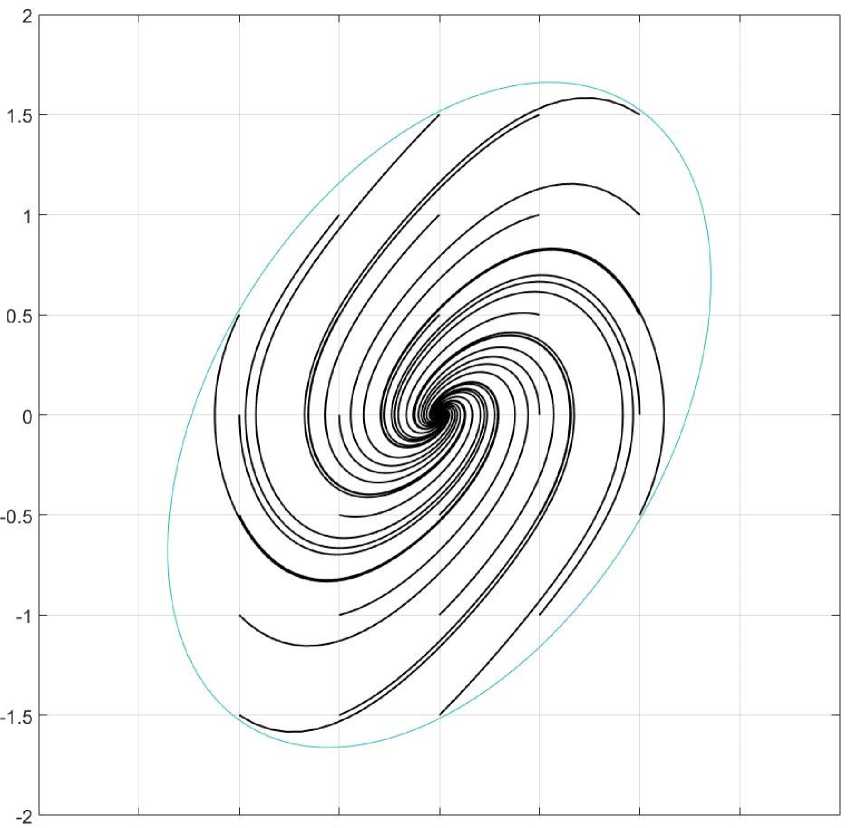
Рис. 3. Фазовые траектории системы при всех выбранных начальных состояниях. Цветом выделен эллипс, ограничивающий область притяжения положения равновесия

Рисунок, полученный по результатам проведения вычислительного эксперимента, показывает, что все траектории, которые начинаются внутри эллипса, стремятся к нулевому положению равновесия.

Таким образом, оценка области притяжения положения равновесия корректна.

Заключение. В работе была рассмотрена нелинейная система, которая имеет по-

квадратичной формы и показано, что нулевое положение равновесия является асимптотически устойчивым. Для оценки области притяжения положения равновесия была составлена оптимизационная задача, для которой было найдено приблизительное решение. Проведенные вычислительные эксперименты продемонстрировали корректность найденной области

ложение равновесия в начале координат. Была найдена функция Ляпунова в виде

притяжения.