Построение оптимальных древовидных сетей

В настоящей работе рассматривается задача, с разрывными функциями стоимостей на. ребрах, приводится постановка, задачи и ее частные случаи, описан специальный алгоритм полного перебора, всех деревьев и промежуточных однокорневых поддеревьев полного графа, основанный на сформулированных правилах: Правиле расстановки пометок и Правиле подключения. Для формирования точного решения задачи в процессе работы алгоритма, перебора, деревьев и поддеревьев используются правила, отбраковки, основанные на. свойствах оптимального решения, заведомо неоптимальных решений, в результате чего перебор значительно сокращается.

2.    Постановка задачи построения сети с разрывными функциями стоимости на ребрах

Пусть задано множество источников сырья J = {1, 2, 3,..., п} с известными объемами сырья b j > 0 и с ток qo. На множестве W = J U {qo} задан полный граф возможных коммуникаций U(W ). Стоимость соединения двух произвольных вершин этого графа c^j (x tj ) является разрывной функцией, зависящей от величины потока сырья x tj между этими вершинами:

С tj (x tj ) = (x ij + V tj (x tj )) * sign(xij).

(с) Злотов A. В., 2020

(ф Федеральное государственное автономное образовательное учреждение высшего образования

«Московский физико-технический институт (национальный исследовательский университет)», 2020

Будем в дальнейшем рассматривать аппроксимирующую снизу функцию сгз ($гз ) = О^з + ^гз * ^гз ) * sign^), где вгз,игз > 0 — некоторые постоянные коэффициенты.

На рис. 1 представлено её графическое представление.

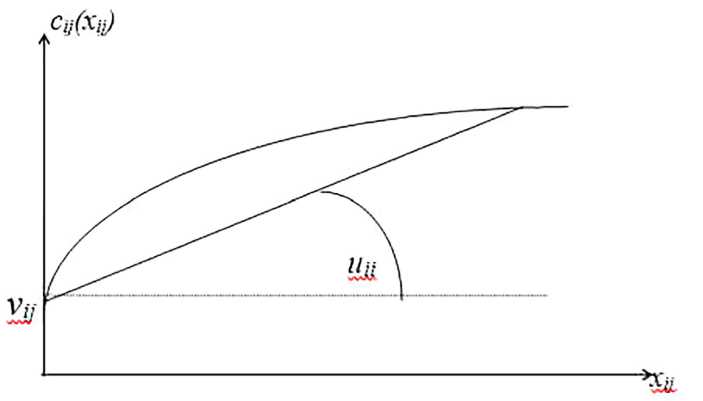
Рис. 1. Функция стоимости ребра сети в зависимости от потока по этому ребру

Требуется построить сеть минимальной стоимости, связывающую множество источников J со стоком до, при условиях полного перетока сырья из источников в сток. То есть необходимо минимизировать величину:

ЕЕ(игз + игз • $гз) • sign^) ^ min(1)

гЕЛ jEW при условиях

(хгз $зг) = bj,      j = 1,2,3,..., п,(2)

гEW

Хгз > 0.(3)

Задача в данной постановке характерна для решения ряда прикладных задач построения различных коммуникационных сетей: трубопроводных, транспортных, сетей связи и других, когда стоимость коммуникации складывается из постоянных затрат игз на ее строительство и «эксплуатационных» затрат и_гз, зависящих от величины потока по данной коммуникации [1].

Примечание. Будем в дальнейшем без ограничения обгрности предполагать, что U (Ж) — неориентированный граф, т.е. и_гз = из_г, и_гз = изг, хотя для ориентированных графов все нижеописанные свойства оптимальных решений и алгоритмы их построения сохраняются с небольшими модификациями.

Справедлива следующая

Лемма. Решение задачи (1)-(3) лежит на множестве всех деревьев полного графа U (Ж).

Если все и_гз = 0, то Задача 1 сводится к известной задаче отыскания кратчайших путей по матрице ^игз || от множества источников J до стока до, для решения которой разработан ряд эффективных алгоритмов [2, 3]. Если все и_гз = 0, то Задача 1 представляет собой задачу построения кратчайшей связывающей сети (КСС) на множестве Ж, алгоритмы решения которой также хорошо разработаны [4, 5].

В общем же случае, когда игз = 0 и игз = 0, данная задача представляет собой многоэкстремальную задачу дискретного программирования, которая является частным случаем сетевой постановки транспортной задачи с фиксированными доплатами.

Комбинаторная постановка задачи 1.

Пусть D — {d k }, к — 1, 2, 3,..., (н + 1)^п-1 — множество всех деревьев полного графа П(W). Стоимость Р(d k ) произвольного дерева определяется по формуле:

^{Р (d} k ) — 5    ^(v ij ⁺ ^ ij • ^x ij ^).

( ij' )E d _k

Потоки X ij >  0 по дугам этого дерева удовлетворяют условиям полного перетока сырья из источников в сток:

5 ^(x ij ^х ji ) — b j      V j E J.

( ij )E d _k

Требуется найти do G D с Р (dg) — minP (d)

d e D

Введем некоторые обозначения.

Пусть J_f — (ф, І 2 ,І з , ... ,Д) ^— некоторое подмножество источников J_f G J и на множестве W_f — J_f U {^o} построено поддерево Rg.

P_s — W \W_f — множество не присоединенных вершин;

^f — путь по поддереву R g от вер шипы г до стока qg:

I f o — 52 ⁿij ~ «Длина пути» ^f по поддереву R g;

PfP^i

• —ij ~ «длина кратчайшего пути» между вершинами г и j по матрице Vij;

  ^jo^—

  ( ^jqo

  
  

  при j G J_s, при j G P_s;

  
  

• xi — значение потока через г-ю вершину;

• y_ij — значение по тока по звену (ij);

3.    Анализ свойств оптимального решения

D s — {d f. } ^— множество всех деревьев dk таких, что R_f G dk;

^(d^s_k) — 52 (v ij + ^ ij * d ij ) — стоимость дерева df.

(i,j)cd=

Требуется определить dg — оптимальное решение Задачи 1 при зафиксированном поддереве R^s G df: ^(df) — min ^(df).

^o            d= e D ₃

При анализе свойств оптимального решения предполагается, что известно некоторое зафиксированное поддерево R_f G dg и необходимо достроить данное поддерево оптимальным образом. В качестве поддерева Rg может выступать одиночная вершина-сток qg.

Функция подключения. Определим функцию Fi(xi,w, R_f ) как «функцию подключе ния» г-Д вершины к подмножеству вершин w С W:

F(x i ,w, R f ) — <

^v ij ⁺ (P ij ⁺ ^ j O) • ^x i min [vij + (u ij + U j o) • Xi] j e w \ i

при ij G R f , i G Wf, при i G P_f.

Функция подключения F i (x i ,w, R_f ) обладает следующими свойствами:

• 1.    F i (x i ,w, R_f ) — монотонно-возрастающая, кусочно-линейная функция по х.

• 2.    У^ F i (b i , W, d k ) = Р(d k ), т.е. F i (b i ,w,d k ) является членом разложения стоимости де- i e J

• 3.    Функция подключения является нижней оценкой стоимости всех деревьев, построенных при зафиксированном поддереве R_f:

рева, dk- соотнесеппым к г-Д вершине.

52 F i (b i W, Rf) 6 Р(d k ) при R f G d k . i e J

Определим множество р® как множество вершин j Е W, на которых достигается минимум функции подключения Ft(xt,w,R_s ).

Теорема 1. О недопустимом пути. Если для каких-либо вершин г и j Е P_s выполняется условие

Ft (b , Ws, Rs ) < min^k) + (u-ij + -j 0) • bt ,                         (6)

kew то в оптимальном решении, построенном на зафиксированном поддереве Rs Е ^0, путь из вершины г к стоку qo не может проходить через вершину j.

Следствие. На основании этого свойства можно оценить значение максимально возмож

Е bf

ного потока Xjm) который может проходить через j-ю вершину в решении ^0: Xjm teP’ где Pj — множеств о тех вершин г Е Ps, для которых не выполняется условие (6).

На рис 2. представлен вид функции подключения в зависимости от потока через г-ю вершину.

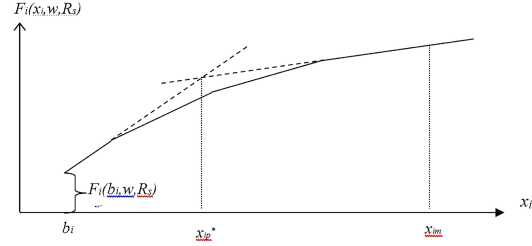
Рис. 2. Функция подключения г-й вершины в зависимости от потока

Теорема 2. Достаточные условия оптимальности подсоединения. Для того чтобы ребро (i,j); г Е Ps, j Е Ws входило в решение ^0; достаточно выполнения 'усло вий

Г Ft (bt ,W,Rs ) = Ui₃ + (utj + Z^so) • bt , { Ft ^(xtm, ^W->^Rs ) = ^tj ^{+ (u}tj ^{+ l}jo ) • ^xtm.

Теорема 3. Необходимое условие вхождения подсоединения в оптимальное решение. Для того чтобы ребро гД, г Е P_s, j Е W _s; могло входить в решение ^ 0_; необходимо выполнение условия j Е р®? ^т-^е- ^оно должно принадлежать множеству вершин, на которых достигается минимум функции подключения г-й вершины.

Теорема 4. Об оценке подсоединения. Погрешность оптимального решения с зафиксированным поддеревом Rs1 = Rs и(Д); г де г Е Ps, J Е Ws по сравнению с оптимальным решением при зафиксированном поддереве Rs не превосходит значения dtj = max{ ^jj + (utj + U^) • bt - Ft(bt, W, R®)], [vtj + (utj + ljo) • Xtm — В(xm, W, Rs)] }• (8)

4.    Алгоритм полного перебора всех деревьев и промежуточных однокорневых поддеревьев

Алгоритмы точного решения задачи строятся на базе алгоритма полного перебора всех деревьев и промежуточных однокорневых поддеревьев полного графа U (W). Алгоритм перебора должен удовлетворять следующим требованиям:

• 1.    Полный перебор без повторов не только всех деревьев, построенных на множестве вершин W, но и всех промежуточных поддеревьев с корнем в зафиксированной вершине qo.

• 2.    Конструктивность способа формирования деревьев и поддеревьев путем последовательного «наращивания» ребер.

Ниже описывается алгоритм перебора, удовлетворяющий перечисленным требованиям и реализованный в алгоритмах точного решения задачи.

В процессе перебора последовательно строятся поддеревья различных «уровней». На S-м уровне 1 <  S < п + 1 формируются деревья R_s, содержащие S вершин.

Процесс построения деревьев осуществляется последовательным движением вдоль ряда поддеревьев: производится переход от уровня к уровню (от 1-го и до (N+l)-ro). Причем поддеревья верхнего уровня отличаются от образующего поддерева нижнего уровня добавлением только одного ребра. На каждом S-м уровне образуются не сразу все поддеревья из S вершин, а лишь некоторая, однозначно определенная алгоритмом, часть их. После того, как будет получена часть деревьев (п + 1)-го уровня, происходит возврат к п-му уровню и из него образуются новые деревья (п + 1)-го уровня. Если образование новых деревьев (п + 1)-го уровня окажется невозможным, то производится возврат к (п — 1)-му уровню и образование из него новой п-й, а за тем и (п + 1)-й группы деревьев.

Процесс заканчивается, когда просмотрены все поддеревья 2-го уровня.

Опишем переход от г-го уровня к (г + 1)-му уровню.

Пусть из г — 1-го уровня образован г-й уровень и из него не обходимо образовать (г + 1)-й уровень.

На г-м уровне имеется множество вершин J_т = {Ji,j2,...,і Т }, образующих поддерево R_т. Этому J_т соответствует множество пометок Е_Т = {еТ, е2,..., е Т }. Остальные вершины образуют множество не присоединенных вершин Р_Т = {рТ ,р₂, ••• ,Р п +1_-т }•

Алгоритм перебора основывается на «Правиле подключения» и «Правиле расстановки пометок», которые формулируются следующим образом:

Правило подключения: Произвольная вершина рТ Е Р_Т может быть подсоединена к вершине УТ поддерева R _т только в том случае, если ее ікшер больше пометки вершины j ^; Р^Т > ^ек-

Правило расстановки пометок: При подключении произвольной вершины рТ Е Р_т к вершине УТ поддерева R_т она получает пометку, равную 0. Все вершины по пути от данной вершины к корню поддерева получают пометку, равную номеру вершины, подсоединенной к данной, по этому пути. Остальные вершины получают пометку, равную некоторому боль шому числу М >  п.

Путь от последней подключенной вершины до корня дерева будем называть «генерирующим путем».

В начальный момент работы алгоритма г = 1, Ji = qo, Р = J, Ei = {0}.

Пусть г = п + 1. Это означает, что построено очередное дерево. В этом случае переходят к п-му уровню и пытаются образовать из него новый (п + 1)-й уровень. Если это невозможно, то переходят к (п — 1)-му уровню для образования из него нового п-го уровня и т.д.

Опишем этот процесс в общем виде.

Пусть из (г + 1)-го уровня оказалось невозможным образование (г + 2)-го уровня. В этом случае производится переход к г-му уровню для образования из него нового (г + 1)-го уровня. На г-м уровне для вершины рТ на генерирующем пути среди меток с индексом к > к_Т ищется метка е >  р Т

Если такая метка найдена, то соответствующий ей номер фиксируется в качестве нового значения к_Т н производится переход к (г + 1)-му уровню.

Если для рТ. не было найдено такой метки, то рассматривается следующая вершина р ^Т +1- значение к_Т полагается равным нулю н опять ищется метка е с е < р ^Т₊i-

Если ii + 1 станет равным п — г. т.е. просмотрены все вершины множества р_Т. производится возврат к ( г — 1)-му уровню для образ*шання из него нового г-го уровня.

Процесс заканчивается, когда из начального уровня г = 1 не удается построить следующий уровень.

Данный алгоритм реализует полный перебор без повторов всех деревьев и однокорневых поддеревьев на множестве вершин W.

Правило формирования следующего уровня путем подсоединения одного ребра служит конструктивным приемом построения ряда поддеревьев, упорядоченных по включениям

R1 С R2 С ... R_n С R n +h что облегчает их анализ и отбраковку в алгоритме точного решения.

На рис. 3 проиллюстрирована работа алгоритма перебора на очередном шаге алгоритма.

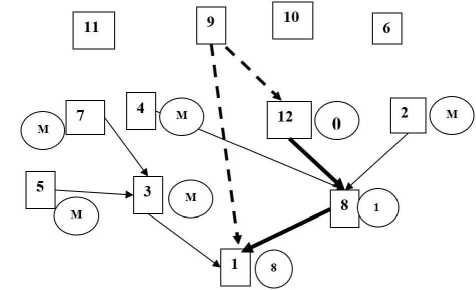
Рис. 3. Иллюстрация работы алгоритма перебора

Здесь: {1, 2, 3, 4, 5, 7, 8,12} — вершины поддерева;

J_s = {1, 2, 3, 4, 5, 7, 8,12}, P_s = {6, 9,10,11};

{8, М, М, М, М, М, 12, 0} — текущие помсткіі этих вершин, где М — большое число М > 12;

{12} — последняя подсоединенная вершина;

{1, 8,12} — генерирующий путь;

Ребра (9,12), (9,1) — возможные подключения 9-й вершины к генерирующему пути.

Рис. 4 иллюстрирует работу алгоритма перебора для четырех вершин.

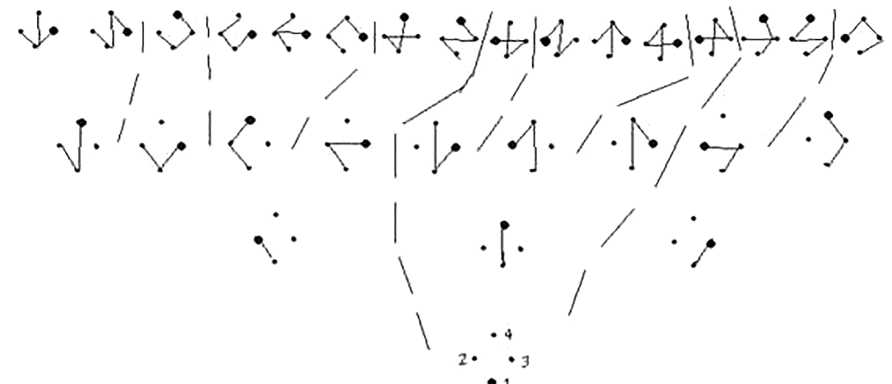
Рис. 4. Все деревья и однокорневые поддеревья для четырех узлов

5.    Алгоритмы построения оптимальных древовидных сетей с разрывными функциями стоимости на ребрах

Для решения этих задач разработаны следующие основные алгоритмы:

• 1.    Алгоритм формирования начального поддерева.

• 2.    Алгоритм полного перебора всех деревьев и промежуточных однокорневых поддеревьев (описанный в предыдущем разделе).

• 3.    Алгоритм точного решения задачи построения сети (1)-(3).

• 4.    Модифицированный алгоритм отыскания точного решения.

• 5.    Алгоритм получения начального приближения.

• 6.    Алгоритм корректировки начального приближения.

Алгоритм формирования начального поддерева Ro. Этот алгоритм используется как в точном, так и в приближенном алгоритмах решения задачи и служит для формирования поддерева Ro с корнем в стоке qo, которое заведомо входит в оптимальное решение задачи do: Ro С do. Для некоторых задач этот алгоритм может сразу построить оптимальное решение Ro = do. В частности, точное решение получается в предельных случаях — в задаче построения кратчайшей связывающей сети (v -j = 0) и в задаче отыскания маршрутов наименьшей стоимости ( v -j = 0).

Алгоритм построения начального поддерева основывается на правилах, при помощи которых на каждом шаге алгоритма определяется очередное звено (i,j) добавляемое к уже построенной части поддерева.

Предварительно по матрице ^ i)ij || вычисляется матрица «кратчайших расстояний» ^d ij |. Далее на каждом шаге алгоритма пока это возможно для всех не подсоединенных вершин по правилам (6), определяется вектор максимально возможных потоков ||аф_т|| и в случае выполнения для какой-либо вершины условия оптимальности (7) она подключается к уже сформированному поддереву.

Алгоритм точного решения задачи. Алгоритм точного решения задачи основан на направленном переборе всех деревьев полного графа. В процессе перебора используется ряд правил отбраковки, позволяющих не рассматривать большие группы деревьев и промежуточных поддеревьев, в результате чего перебор значительно сокращается. Правила отбраковки основываются на свойствах оптимального решения задачи, описанных в п. 2. В случае наличия ограничений по объему используемой оперативной памяти или времени решения задачи, необходимо применение алгоритмов приближенного решения. Эти алго ритмы описываются в следующем разделе.

При работе алгоритма точного решения задачи используется модификация метода перебора для того, чтобы просматривать все деревья и поддеревья при зафиксированном поддереве Ro. которое сформируется по алгоритм у построения начального поддерева Ro. Необходимая модификация состоит в том, что на каждом шаге алгоритма перебора при расстановке меток е^+1 всем вершинам поддерева Ro приписывается одинаковая метка, равная номеру вершины, подсоединяемой к поддереву Ro по выделенному пути от вершины р- до стока.

Основным аппаратом для отбраковки в алгоритме точного решения является правило отбраковки, основанное на условии допустимости подсоединения (8).

Кроме того, используется правило отбраковки тех поддеревьев Rs, для которых нижняя оценка стоимости оптимального решения на данном поддереве —

W) = ^F i (b i ,W,R_s)

iEJ больше, чем стоимость временно оптимального решения di — tp(di). Для допустимых подсоединений p(d1) > ^(Rs).

Эффективность данного правила отбраковки зависит от того, насколько временно оптимальное решение di близко по стоимости к оптимальному решению do. Поэтому в качестве начального значения для y(di) целесообразно брать решение, получаемое по алгоритму приближенного решения, которое затем может быть улучшено в процессе работы алгорит ма точного решения.

Работу алгоритма точного решения можно представить в виде последовательности следующих этапов:

• 1.    Вычисление матрицы кратчайших расстояний Цгфу|| по матрице Hu ij |ф

• 2.    Построение начального поддерева Ro по алгоритму построения начального поддерева.

• 3.    Определение приближенного решения di и его стоимости y(di) по алгоритму получения приближенного решения.

• 4.    Получение оптимального решения.

Алгоритм приблнЕнсенного решения задачи. Алгоритм приближенного решения можно представить, как последовательность алгоритмов формирования начального поддерева, построения начального приближения и корректировки начального приближения.

Использование совокупности этих алгоритмов позволяет получать хорошее приближенное решение с оценкой абсолютной погрешности получаемого решения.

Алгоритм построения начального приближения. Данный алгоритм работает после алгоритма формирования начального поддерева. Построение приближенного решения проводится последовательным «наращиванием» уже построенной части дерева путем добавления к нему такого звена ( i, j ), i Е Р_Т, j Е W_T, для которого минимальна величина 5ц оценки погрешности на его включение в оптимальное решение, определяемая по формуле (8).

Алгоритм корректировки начального приближения.

В данном алгоритме для всех вершин множества J проверяется возможность их переключения с одновременным уменьшением стоимости решения. Переключение производится для вершины, дающей наибольшее уменьшение функционала. Работа алгоритма заканчивается, когда такого переключения нельзя сделать ни для одной вершины.

В результате последовательной реализации алгоритмов формирования начального поддерева, построения начального приближения и его корректировки будет найдено приближенное решение di Е D. Погрешность полученного решения по сравнению с оптимальным решением не превосходит величины АФ = ^^ [Ғфф, W, di) — Ғ(Ьі, W, Ro)] , т.е. равняется ieJ разности между величиной функционала полученного решения и нижней оценки оптимального решения после сформирования начального поддерева.

Система размещения объектов и коммуникаций. Описанные алгоритмы реализованы в Системе размещения объектов и коммуникаций, которая применяется для решения задач размещения совместно со связывающими коммуникациями [1]. На рис. 5 показан пример применения этой системы для Тенгизского месторождения.

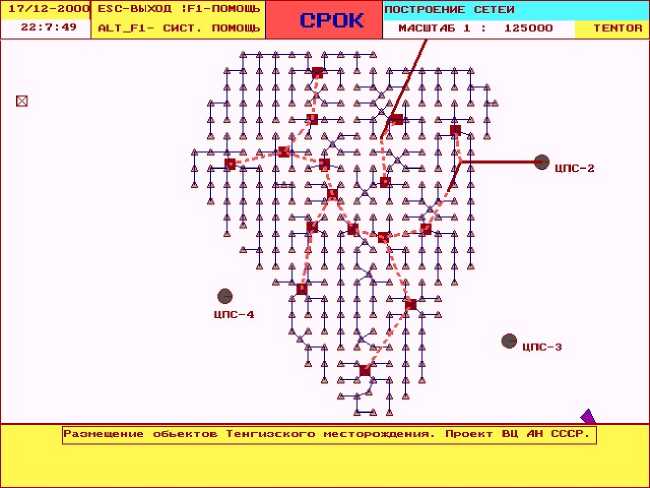
Рис. 5. Тенгизское нефтяное месторождение. Проект ВЦ РАН

Работы по данной проблематике поддержаны в 2012 г. Премией им. Н. К. Байбакова «за большие достижения в решении проблем устойчивого развития энергетики и общества».