Построение параллельной модели многослойного персептрона

Искусственная нейронная сеть (ИНС) – это математическая модель, а также ее программная или аппаратная реализация, построенные по принципу организации и функционирования биологических нейронных сетей – сетей нервных клеток живого организма. Существует огромное количество различных по своим функциональным возможностям и архитектуре классов ИНС (например, многослойный персептрон, сеть Кохонена, сеть Хопфилда и другие).

В настоящее время моделирование ИНС и применение полученных моделей для решения интеллектуальных задач различного уровня вновь становится актуальным. Но с увеличе- нием сложности задачи растет сложность архитектуры соответствующей нейронной сети. Это, в свою очередь, приводит к замедлению обработки сетью данных. Поэтому одним из важнейших аспектов исследования ИНС является эффективное использование растущих с каждым годом вычислительных мощностей. И в первую очередь это выражается в разработке параллельных алгоритмов для ИНС.

В данной статье рассматривается алгоритм построения программной модели многослойного персептрона, основанный на подходе «один нейрон – один процесс». В качестве средства разработки выбран функциональный язык программирования высокого уровня Erlang. Выбор обусловлен в первую очередь тем, что с помощью ИНС возможно решать задачи, требующие на практике высокого уровня надежности. Erlang зарекомендовал себя как удобное и эффективное средство разработки высоконадежных систем за относительно короткие промежутки времени.

К наиболее важным характеристикам Erlang можно отнести следующие [3]:

• -    краткость и простота – программы на Erlang намного короче и проще, чем те же самые программы на императивных языках (например С);

• -    отсутствие побочных эффектов – оператор присваивания отсутствует, объекты нельзя изме-

• нять и уничтожать, можно только создавать новые путем декомпозиции и синтеза существующих;

• -    отказоустойчивость – язык обладает множеством механизмов для обеспечения отказоустойчивости создаваемых программ, к примеру, в случае отказа одного из узлов виртуальной машины Erlang его процессы начнут исполняться на других и вернутся обратно при восстановлении работоспособности узла;

• -    «горячее» обновление кода – программы на Erlang позволяют обновлять свой код прямо во время исполнения, предусмотрена также возможность автоматического отката обновлений в том случае, если они приводят к нарушению работы системы;

• -    инкрементная загрузка кода – пользователь может управлять загрузкой модулей в память при исполнении программы.

Архитектура параллельной модели многослойного персептрона

Как было упомянуто выше, при разработке программы использовался принцип организации ИНС «один нейрон – один процесс». Под процессом в данном случае понимается легковесный процесс виртуальной машины Erlang, а не процесс операционной системы. В нем инкапсулированы все операции, которые в соответствии с математической моделью, предложенной в 1943 г. Мак-Каллоком и Питтсом, должен выполнять искусственный нейрон (см. рис. 1), а именно: на основе входных сигналов от других нейронов, связанных с данным по входу, вычислить выходной сигнал и отправить его всем нейронам, связанным с данным по выходу, в случае прямого функционирования нейронной сети [2], а также ряд дополнительных операций, необходимых для организации процесса обучения ИНС, на чем остановимся позже.

Необходимость в интенсивном обмене сообщениями между нейронами обусловливает использование возможностей OTP – набора Erlang-библиотек. Для реализации внутренней логики процессов нейронов было использовано так называемое behaviour gen-server, представляющее собой middle-ware, инкапсулирующее внутри функции, необходимое для реализации обобщенной клиент-серверной логики, а также предоставляющее callback-интерфейс для задания специфических обработчиков основных событий данного behaviour. Gen_server позволяет создавать обработчики для синхронных и асинхронных обменов сообщениями. Поскольку син- хронный обмен, как правило, замедляет работу системы из-за блокировок ожидания завершения обработки, рассматриваемая модель нейрона была реализована с использованием асинхронных обменов сообщениями [4].

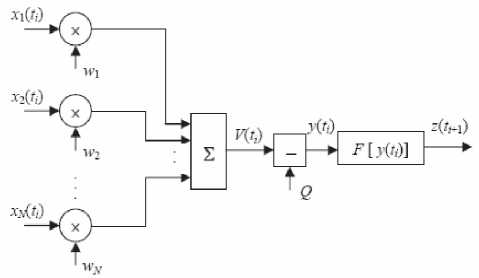
Рис. 1. Схема искусственного нейрона

Элементарные функции, выполняемые нейроном, – это лишь первый уровень абстракции. Рассматриваемый класс нейронных сетей (многослойный персептрон) предполагает наличие операций, специфических для некоторых групп нейронов (слоев), поэтому возникает необходимость ввести дополнительный уровень абстракции – непосредственно многослойный персептрон (MLP). Данная сущность модели также реализована как behaviour gen_server с использованием асинхронного обмена сообщениями. MLP обменивается сообщениями с сущностями нижележащего уровня абстракции – нейронами, – выполняя функции диспетчера.

MLP запускается как отдельный процесс, который контролирует все операции (вычисления и обмен сообщениями), выполняемые в процессе как работы, так и обучения ИНС. При запуске системы MLP получает исчерпывающую информацию об архитектуре нейронной сети и на ее основе запускает дочерние процессы – NEURON (см. рис. 2).

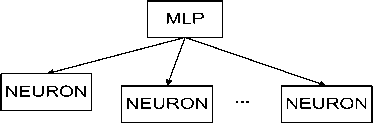
Рис. 2. Схема взаимосвязи уровней абстракции параллельной модели многослойного персептрона

Остановимся подробнее на алгоритме организации взаимодействия между процессами внутри модели. Особое внимание следует уделить обучению ИНС, поскольку это наиболее ресурсоемкий и важный процесс, определяющий дальнейшую эф- фективность работы нейронной сети. Кроме того, процесс прямого функционирования ИНС является составной частью процесса обучения, поэтому отдельно останавливаться на нем не будем.

Для реализации прототипа был выбран стохастический алгоритм обучения с учителем RPROP, основанный на принципе обратного распространения ошибки и вычислении градиента функции ошибки нейронной сети [1]. В основе алгоритма лежит положение о том, что сутью обучения сети является минимизация функции ошибки вида

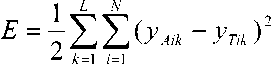
где y_Aik - фактический выходной сигнал нейрона i , y_Tik - желаемый выходной сигнал нейрона i , / = 1Л - число нейронов выходного слоя, к = 1,Z - размер обучающей выборки. Коррекция весовых коэффициентов сети осуществляется в соответствии с формулой:

wkA=wk-\w          (2)

Г\-\ 1             rV                   J                                            x / где Wk – весовые коэффициенты сети на текущем шаге, Wk+1 – весовые коэффициенты сети на следующем шаге, bw – матрица приращений весовых коэффициентов. Приращение весовых коэффициентов вычисляется на каждом шаге следующим образом:

min( Az/(Z - 1) -// + ,Amax ), если

SE        dE-----(/ - 1) •-----(Z) > 0;

dw у        Swуmax( b^t- 1) •//", Amm ), если d w у        5 w

0E

^^wu = - ^u "Sign (д---(0).

5 ^w у

Начальные величины приращения Δ_l⁽⁰⁾ выбираются случайно из промежутка (0; 1). Параметры Δ_min = 10^-6 и Δ_max = 50. Константы η ⁺ = 1,2; η ^- = 0,5. Организация взаимодействия отдельных сущностей системы в процессе обучения ИНС по вышеописанному алгоритму представлена на рис. 3.

В соответствии с алгоритмом обучение длится некоторое заранее определенное количество эпох. Каждая эпоха представляет собой последовательность операций по вычислению корректировки весов и смещений сети, описанную выше. Останавливается обучение при выполнении условий одного из критериев останова. Наиболее значимым является критерий достижения заданной минимальной ошибки (для его проверки на каждом шаге на основе данных обучающей выборки вычисляется текущая среднеквадратичная ошибка сети). Критерием, заключающим время обучения в разумные рамки, является завершение заданного количества эпох. Подобное ограничение позволяет избежать зацикливания процесса обучения, что, однако, не дает гарантий достижения оптимального уровня ошибки.

Каждый блок на приведенной схеме соответствует набору операций, выполняемых в ответ на определенное сообщение. Стрелками показаны направления движения сообщений. Область с заголовком NEURON соответствует уровню абстракции NEURON, внутри которого запущены процессы Neuronm, соответствующие нейронам сети. Внутри каждого такого процесса предусмотрены реакции на такие сообщения, как send_signal (инициирует вычисление состояния и выхода нейрона), calc_grad (инициирует вычисление градиента функции ошибки в пределах одного нейрона) и correct_wb (инициирует пересчет весов и смещений для связей одного нейрона). Следует отметить, что инициируются операции, соответствующие указанным сообщениям, на уровне абстракции MLP. Поскольку обмен сообщениями асинхронный, возникает необходимость введения дополнительных индикаторов завершения процессов обработки сигналов. В данном случае это касается операций simulate, calc_grad и correct_wb, которые завершаются на уровне MLP только тогда, когда получено необходимое количество откликов от процессов уровня абстракции NEURON. В частности, операция simulate завершается тогда, когда получено количество сообщений sim_end, равное количеству выходных нейронов сети, что соответствует завершению вычислений всех выходов ИНС.

После завершения обучения мы получаем готовую к работе сеть с настроенными весами и смещениями, сохраненными во внутреннем состоянии behavior gen_server.

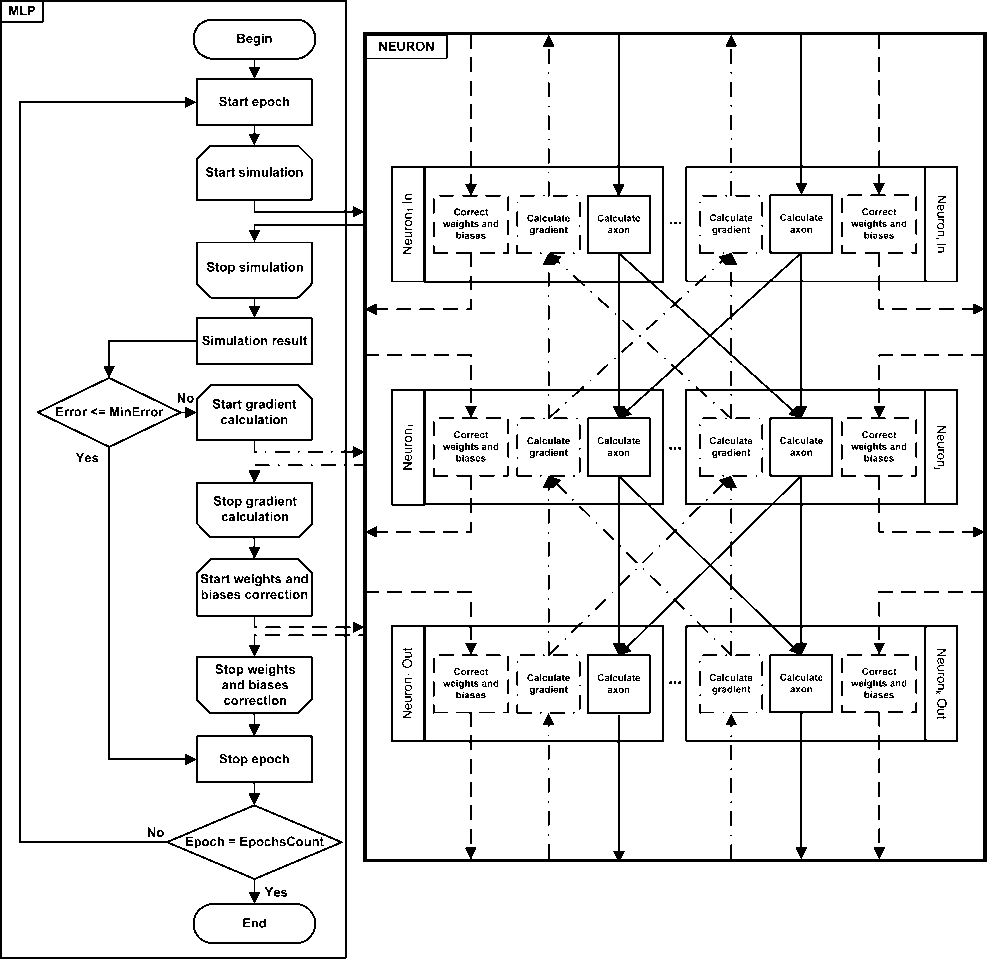
Рис. 3. Организация взаимодействия сущностей системы на уровнях абстракции MLP и NEURON

Тестирование прототипа

Для анализа эффективности разработанного прототипа было произведено тестирование производительности. Условия тестирования приведены в таблице 1.

Указанные особенности архитектуры и обучающей выборки обусловлены прежде всего тем,что сеть конструируется для дальнейшего решения задач,связанных с биометрической идентификацией (аутентификацией). Задачи данного рода требуют высокой точности, что приводит к необходимости оперирования бинарными данными больших размерностей.

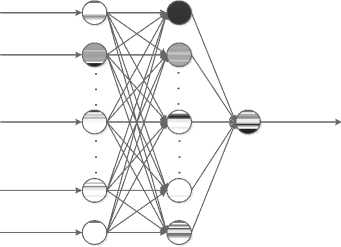
Рис. 4. Обобщенная архитектура исследуемого многослойного персептрона

Таблица 1. Условия тестирования прототипа

Архитектура многослойного персептрона	Структура слоев: -    N входов; -    1 скрытый слой с количеством нейронов N; -    1 выход. Активационная функция скрытого слоя: сигмоидальная Активационная функция выходного нейрона: линейная 100 < N < 500
Характеристики обучающей выборки	Объем: М пар Особенности: бинарные данные 10 < М < 50
Процессор	Intel(R) Xeon(R) CPU Х5650 @ 2.67GHz
Максимальное количество вычислительных узлов	8
Операционная система	CentOS release 6.2 (Final) Linux version 2.6.32-220.el6.x86_64
Версия      программного обеспечения	Erlang R15B (erts-5.9)

Обобщенная схема исследуемой сети приведена на рис. 4. Основным критерием качества прототипа является среднее время обучения сети – это величина, равная отношению общего времени, затраченного на обучение нейронной сети, к количеству эпох, которое на это ушло. Следует отметить, что скорость работы прототипа зависит от нескольких из- меняемых параметров: размерность задачи (а следовательно, размерность самого многослойного персептрона), размер обучающей выборки, а также количество вычислительных единиц (в данном случае ядер процессора). То есть зафиксировав один из параметров, мы получим диаграмму зависимости скорости обучения от двух других.

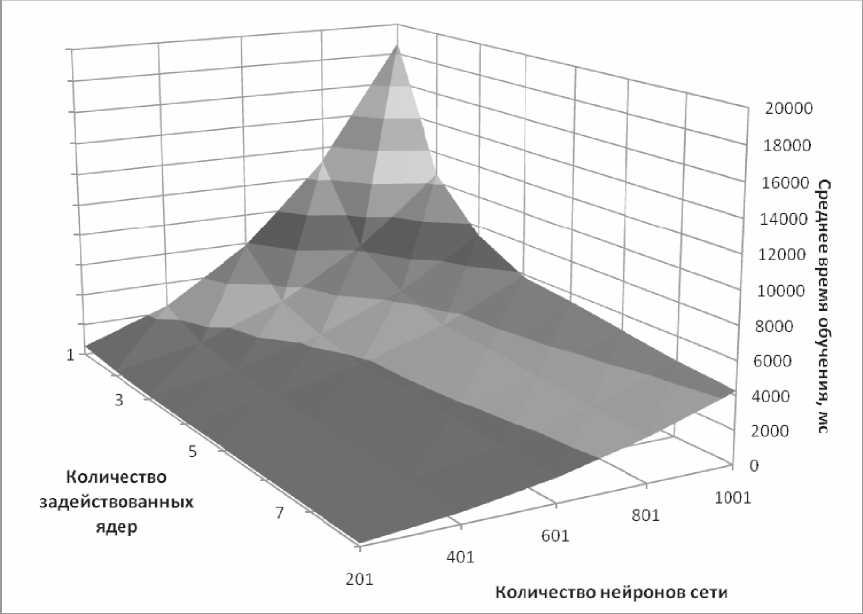
Рис. 5. Зависимость среднего времени обучения многослойного персептрона от числа задействованных ядер и числа нейронов сети

В первом тесте, зафиксировав размер обучающей выборки (20 пар), мы получили результаты, изображенные на рис. 5.

Как и следовало ожидать, с увеличением количества ядер среднее время обучения сети уменьшается, причем это тем более значимо, чем больше размер сети. Зависимость среднего времени обучения от количества задействованных ядер при фиксированном размере сети не является линейной, что говорит о наличии некоторого предела роста эффективности с ростом вычислительной мощности. Например, для размера сети в 1001 нейрон на интервале от шести до восьми ядер скорость обучения растет медленнее, чем на интервале от одного до пяти ядер.

Также следует отметить, что для восьми ядер с ростом размера сети среднее время обучения растет медленнее, чем для одного ядра. А зависимость среднего времени обучения от размера сети при фиксированном количестве ядер близка к экспоненциальной (то есть растет быстрее, чем линейная функция). Во втором тесте, зафиксировав размер сети (201 нейрон), получили результаты, изображенные на рис. 6.

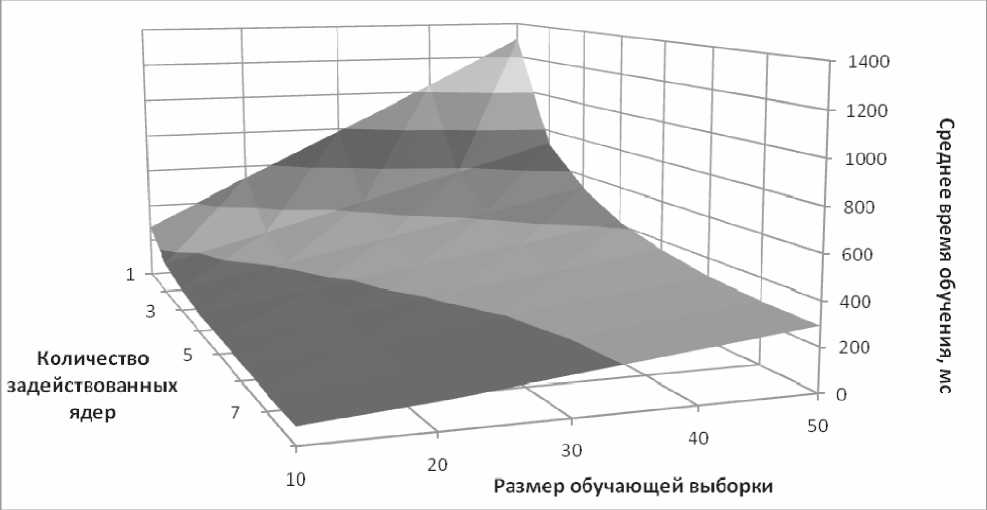
Рис. 6. Зависимость среднего времени обучения многослойного персептрона от размера обучающей выборки и числа задействованных ядер

Исходя из графика можно сделать вывод, аналогичный предыдущему. Однако зависимость среднего времени обучения от размера обучающей выборки носит линейный характер. Угол наклона прямой при этом тем меньше, чем больше количество задействованных при расчете ядер.

На рис.7 приведена диаграмма загрузки ядер процессора во время обучения многослойного персеп-трона.Она демонстрирует эффективность использования вычислительных ресурсов (ядра загружены практически на 100% и не простаивают)при выполнении обработкиданных разработанным прототипом.

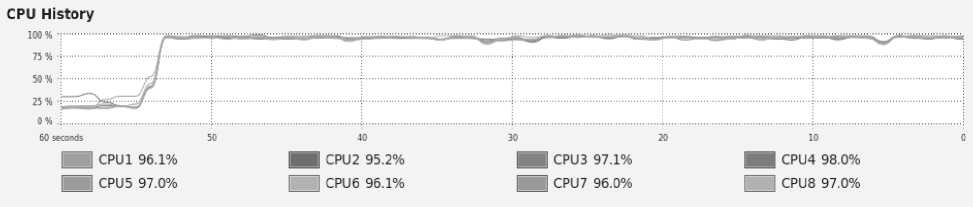
Рис. 7. Степень загрузки ядер процессора во время обучения многослойного персептрона

Помимо данных по производительности процесса обучения многослойного персептрона во время тестирования собиралась информация по производительности процесса функционирования ИНС. В данном случае мы можем построить зависимость времени работы сети от числа задействованных ядер и количества нейронов. Соответствующий график приведен на рис. 8. На нем можно проследить ту же тенденцию сокращения времени работы, а также сокращения темпа роста времени работы с ростом размера сети при увеличении числа задействованных ядер.

Заключение

По результатам проведенного исследования можно сделать следующие выводы. Разработанный прототип позволяет использовать преимущества функционального подхода к реализации математических моделей ИНС, что позволяет сократить время работы алгоритма и повысить эффективность использования вычислительных ресурсов. Кроме того, модификация алгоритма за счет ручной синхронизации операций процесса обучения ИНС позволяет использовать преимущества асинхронного обмена сообщениями.

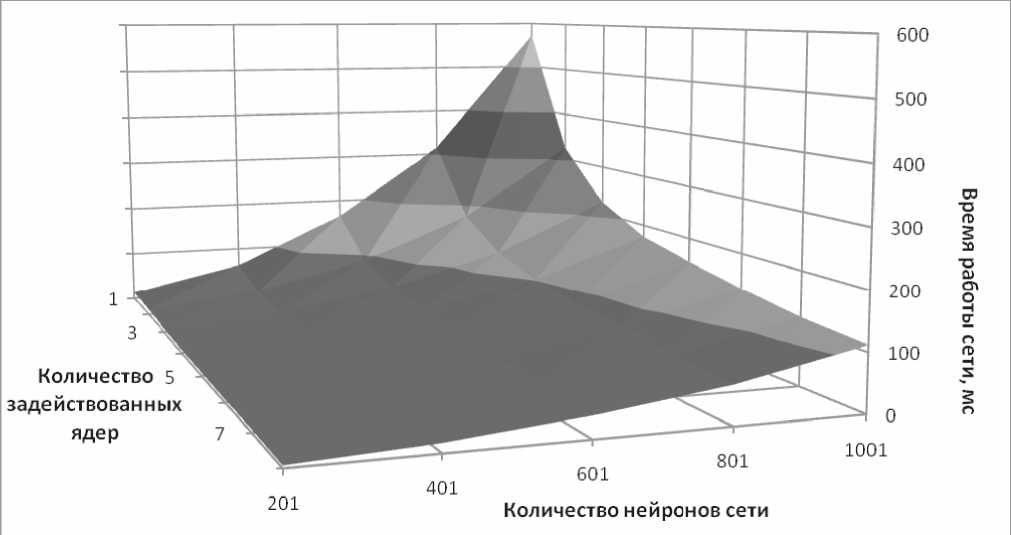
Рис. 8. Зависимость времени работы многослойного персептрона от числа задействованных ядер и числа нейронов сети

Графики, построенные по результатам исследования, показывают тенденцию сокращения времени работы при увеличении количества вычислительных узлов. При этом установлены следующие виды зависимостей:

• -    между средним временем обучения (а также временем непосредственной работы сети) и размером сети носит экспоненциальный характер;

• -    между средним временем обучения и размером обучающей выборки – практически линейна.

Следует также отметить, что приведенная реализация алгоритма позволяет достичь оптимального уровня ошибки.

По результатам всех проведенных экспериментов среднеквадратичное отклонение резуль- тирующих выходов сети от желаемых (ошибка ИНС) в среднем составляет 0,1%.