Построение параллельных алгоритмов поведения программных агентов методами генетического программирования
Автор: Кольчугина Елена Анатольевна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии компьютерных систем и сетей
Статья в выпуске: 3 т.10, 2012 года.
Бесплатный доступ
Предложен способ создания параллельных алгоритмов на основе матричной промежуточной структуры с использованием описания алгоритма в виде древовидной структуры. Введены операции над древовидными структурами, позволяющие получать параллельные алгоритмы методами генетического программирования. Выделены и рассмотрены логические уровни, на которых протекает эволюция алгоритмов поведения программных агентов.
Параллельный алгоритм, генетическое программирование, программный агент, эволюция
Короткий адрес: https://sciup.org/140191567
IDR: 140191567 | УДК: 004.42
Текст научной статьи Построение параллельных алгоритмов поведения программных агентов методами генетического программирования
Одним из способов создания самоорганизующихся программных систем является применение такого класса моделей теории искусственной жизни, как создание искусственных миров. Программная система при этом представляет собой совокупность независимых активных единиц – агентов, которые, находясь в специальным образом устроенной среде, постепенно адаптируются к ней, подобно живым организмам в природе. Адаптация происходит либо путем изменения самого агента, либо путем подстройки его параметров, например весов нейронной сети. В первом случае говорят об эволюции, во втором – об обучении. Критерием успешности адаптации отдельного агента служит значение счетчика «внутренней энергии», определяющее количество процессорного времени, в течение которого возможно продолжение выполнения агента. Следствием высокой приспособленности агента является появление у него «потомков», что приводит к появлению сообщества агентов с идентичным или схожим генотипом. В настоящей работе рассматривается модель, в которой агенты не имеют нейронной сети и развиваются путем эволюции алгоритма поведения агента, протекающей на нескольких уровнях.
Общая структура программного агента
Основные поведенческие свойства программного агента и параметры его состояния задаются последовательностью чисел, которую можно рассматривать как цифровую ДНК [1].
Часть этой последовательности задает макроалгоритм поведения программного агента. При этом номера позиций в последовательности идентифицируют блоки поведения, или элементы макроалгоритма, а значения элементов последовательности определяют программные реализации блоков поведения. Каждая программная реализация блока поведения представляет собой относительно независимую программную единицу, имеющую типовой интерфейс, на уровне которого и происходит взаимодействие с другими единицами.
В состав последовательности чисел, задающей цифровую ДНК, входит подпоследовательность, определяющая значения переменных состояния агента. При этом значения переменных можно рассматривать как нуль-аргументные функции, или как поведенческие блоки, реализующие операции присваивания значений переменным. Как и в случае кодирования алгоритма, номера позиций в последовательности чисел будут однозначным образом соответствовать переменным.
Цифровую ДНК в простейшем случае можно рассматривать как представление линейного алгоритма поведения агента, установив, например, правило, что блоки поведения будут исполняться в порядке возрастания их номеров. Однако в [1] был предложен другой подход, позволяющий строить на базе линейной цифровой ДНК параллельные алгоритмы поведения агентов. Для этого исходная числовая последовательность, представляющая цифровую ДНК, укладывалась в матрицу, называемую в [1] матрицей расписания. В [1] были предложены операции над матрицами расписаний. Расписание представляет собой промежуточную структуру, на основе которой с использованием примитивов, отражающих отношения последовательности выполнения во времени между подмножествами матрицы расписания, таких как seq (строгая последо- вательность выполнения без пересечений во времени), par (толерантность, или параллелизм) и exec (выполнение одного блока поведения), может быть получено множество различных параллельных алгоритмов. Для получения конкретного параллельного алгоритма необходимо определить конкретный способ прочтения расписания как рекурсивное разбиение исходной матрицы расписания на подмножества.
Далее предлагается и рассматривается метод формирования способов прочтения матрицы расписаний, то есть параллельных алгоритмов, и операции, позволяющие преобразовывать параллельные алгоритмы.
Представление параллельного алгоритма в виде древовидной структуры
Матрица расписаний Q размером mxn представляет собой промежуточную структуру, которую можно рассматривать как прототип параллельной формы алгоритма. При этом номера столбцов являются аналогами пространственных координат, то есть задают номера процессорных элементов, на которых будут выполняться макродействия, или блоки поведения в составе алгоритма программного агента. Количество столбцов матрицы определяет требуемое количество процессорных элементов.
Множество номеров строк задает топологические шкалы времени для элементов матрицы: для двух элементов матрицы, находящихся в одном столбце, % и q^, , при к > 0 будет верно, что q^ всегда заканчивает выполнение раньше начала выполнения ^kYi .
Параллельный алгоритм определяется способом прочтения матрицы расписания, то есть рекурсивным разбиением матрицы на множество матриц меньшего размера, которые также разбиваются на подматрицы и так далее, вплоть до отдельных элементов исходной матрицы. При этом на каждом шаге выполнения разбиения матрица будет разбиваться либо на подмножества строк, либо на подмножества столбцов. Благодаря этому подмножества, образовавшиеся на одном шаге выполнения разбиения, будут находиться между собой в отношении либо seq , либо par , либо exec .
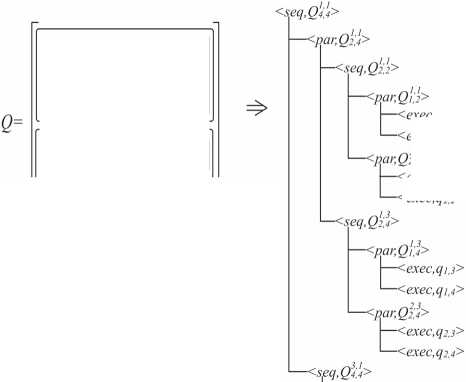
Такое разбиение может быть представлено в виде дерева, корнем которого является исходное расписание, листьями – блоки поведения, а промежуточными вершинами – матрицы меньшего, чем Q , размера, но содержащие более одного элемента. Очевидно, что арность дерева определяется как p < тах{и,т}. Пример такого дерева, а также записи параллельного алгоритма в виде формулы приведен на рис. 1. Для индексации матриц-подмножеств Q используются индексы верхнего левого и правого нижнего элементов матриц в соответствии с их нумерацией в Q .
Дадим рекурсивное определение дерева, соответствующего способу прочтения расписания, то есть параллельному алгоритму:
7г = {(г,0,{П-,...,П;}}|0,
здесь r – отношение между поддеревьями, seq , или exec (для терминальной вершины), Q – матрица расписания, которой соответствует дерево Tr, a Trx,...,Trk – поддеревья дерева Tr, каждое из которых соответствует матрице-подмножеству Q , причемПй=0,йй=5.
— — — — — — — — —
Рис. 1. Построение параллельного алгоритма в виде древовидной структуры и формулы на основе разбиения матрицы расписания
Q
Операции над древовидными структурами Поскольку варианты параллельных алгоритмов представлены в виде множества древовидных структур, для модификации имеющихся алгоритмов и порождения новых можно использовать методы генетического программирования разновидности автоматического программирования, в основе своей родственного генетическим алгоритмам и эволюционным вычислениям [2-3]. В случае генетического программирования каждая хромосома представляет собой программу на подобном языке программирования, например LISP, которая может быть представлена в виде древовидной структуры. Типичный набор операций, используемых в генетическом программировании, включает в себя [2-3]:
- репродукцию;
- кроссинговер;
- мутацию;
- дупликацию и делецию генов;
Репродукцию можно понимать либо как генерацию новой, полностью случайной древовидной структуры, либо как результат применения крос-синговера, или соединения поддеревьев, к двум или более уже существовавшим древовидным структурам-родителям с возможной последующей мутацией. Мутация означает случайную перестройку поддерева исходной структуры. Операции дупликации и делеции, то есть дублирования или удаления генов, представляется более уместным выполнять на уровне матрицы расписаний. Применение делеции и дупликации на уровне древовидной структуры, задающей способ прочтения матрицы расписаний, то есть параллельный алгоритм, способно существенно усложнить задачу выбраковки агентов с нежелательными свойствами. При условии исключения делеции и дупликации, на основе одной и той же матрицы расписаний могут быть построены деревья с одинаковым корнем и листьями, хотя и имеющие различную высоту, сбалансированность и внутренние вершины.
построить _ поддерево (матрица
2) -
дерево begin
Tr
= new
дерево;
if (£Wy) then begin x=rand(); if(^>0.5) then begin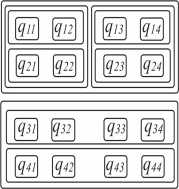
Список литературы Построение параллельных алгоритмов поведения программных агентов методами генетического программирования
- Кольчугина Е.А. Эволюция расписаний как средство разработки параллельного алгоритма поведения цифрового организма//Известия вузов. Поволжский регион. Технические науки. №1(5), 2008. С. 45-52.
- Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы. М.: ФИЗМАТ-ЛИТ, 2006. 320 с.
- Koza J.R., Bennett F.H, Andre D., Keane M.A. Genetic Programming: Biologically Inspired Computation that Creatively Solves Non-Trivial Problems//Evolution as Computation. DIMACS Workshop. Princeton, January 1999. Heidelberg: Springer-Verlag, 2001. P. 15-44.


