Построение помехоустойчивого кода на базе голографического представления произвольной цифровой информации

Голография как метод восстановления волнового фронта может быть использована не только для записи и восстановления трехмерных изображений объекта. Фундаментальное свойство голографии – делимость голограммы [1] (возможность восстановления полного изображения объекта по фрагменту голограммы) – представляет интерес для помехоустойчивого кодирования произвольных сообщений. Свойство делимости может эффективно использоваться при передаче информации по каналу связи с большим уровнем шума и / или при недостаточном уровне сигнала, когда могут быть искажены или утрачены большие фрагменты сообщения.

В этой связи интересен перенос принципов голографической обработки изображений на кодирование произвольных цифровых данных и разработка голо- графических методов помехоустойчивого кодирования, позволяющих корректировать множественные ошибки.

Это актуально для систем Radio-over-fiber (RoF), использующих многопозиционные методы модуляции Х-QAM в оптоволоконных каналах, к которым предъявляются высокие требования с точки зрения необходимого высокого отношения сигнал/шум, низкой дисперсии и других характеристик, которые могут привести к значительным искажениям сигнала и, как следствие, к искажению исходного констелляци-онного созвездия. Таким образом, вышеупомянутое свойство голографии позволит значительно повысить помехоустойчивость сигналов как в волоконных, так и в радиосегментах RoF-систем.

Высокая помехоустойчивость голографического способа обработки информации и способность обнаруживать сигнал, во много раз меньший уровня по- мех, нашли применение в радиоголографии при построении радиолокационных систем [2, 3, 4]. Способы уменьшения загрузки радиоканала при передаче информации для последующего синтеза голограммы 3D-изображений без их недопустимых искажений рассмотрены в работе [5].

Использовать голографическое кодирование для исправления ошибок предложено в [6]. Принципиальным отличием этой задачи от задач обработки изображений, обладающих внутренней избыточностью и допускающих приемлемую потерю точности, является требование точного соответствия декодированного блока данных исходному. Рассмотренный метод основан на представлении исходного цифрового блока произвольных данных как изображения и расчете интерференционной картины волнового фронта, создаваемого этим изображением.

Кодирование информации (моделирование голограммы) и декодирование (восстановление цифрового массива) требует достаточно больших вычислительных ресурсов. Сложность вычислений можно значительно сократить, если использовать для представления исходного блока цифровой информации не двоичный, а единичный позиционный код. В этом случае оптическим объектом, для которого строится голограмма, является точечный источник на черном фоне, а информация закладывается в координаты точки на поле объекта. Результатом кодирования является простейшая голограмма – зонная пластинка Френеля, координаты центра которой несут кодируемую информацию.

В работе [7] доказана возможность использования одномерных радиоголограмм с целью снижения временных и материальных затрат при передаче по радиоканалу. Моделирование голографического кодирования с голограммами разной формы и размера показало, что эффективность кода, использующего матричную голограмму ( m , m ), соответствует эффективности кода с линейной одномерной голограммой с количеством точек m ². Поэтому для снижения вычислительной сложности рационально использовать представление входных данных в виде одномерного массива и формировать линейную одномерную голограмму.

1.    Голографическое кодирование 1.1.    Алгоритм кодирования

Голографический метод кодирования основан на математическом моделировании одномерной голограммы, создаваемой в виртуальном пространстве волной от объекта, представляющего собой входной блок данных [8].

Линейное одномерное голографическое кодирование произвольной цифровой информации отличается от оптической голографии следующими факторами:

• •    объект является одномерным,

• •    объект не привязан к пространственным измерениям, единица измерения размера объекта и голограммы – длина волны излучения,

• •    волна распространяется без затухания и когерентна на любом расстоянии.

Предварительно входной блок цифровых данных X , представляющий собой k -разрядный двоичный код, преобразуется во вторичный блок A – пространственный одномерный объект, состоящий из n =2 ^k точек A ( i ), i = 1,…, n , значение одной из которых равно 1, остальных – нули: A ( i ) = 1 при i= X , A ( i )=0 при i ≠ X . Этим преобразованием закладывается информационная избыточность с числом разрядов r = n – k и задается скорость кода R = k / n . Вторичный блок имеет ( n – 1) нулей и одну единицу в позиции, заданной первичным блоком. Таким образом, входной блок данных используется как адрес позиции единицы в последовательности нулей единичного позиционного кода вторичного блока. В оптической интерпретации объект (вторичный блок) представляет черную линию с одной светящейся точкой, позиция которой определяется кодируемым первичным блоком.

Формирование голограммы производится путем построения зонной линейки Френеля.

Расстояние между точками A ( i ) равно d . Ячейка A ( i ) = 1 является источником сферической волны, распространяющейся в плоскости анализа и характеризуемой длиной волны λ = d .

Рассмотрим значения сферического волнового фронта в плоскости нахождения объекта на линии, расположенной параллельно объекту на расстоянии L , в n точках с шагом d . Волна от источника распространяется без затухания и попадает на все элементы одномерного массива H ( j ), j = 1,…, n . Значения волнового фронта в рассматриваемых точках H ( j ) определяются фазой приходящей волны φ. Значение волны от элемента A ( i ) в точке нахождения элемента голограммы H ( j ) равно

H (i) = A (i )sin ф(i, j), где ф (i, j) - фаза волны элемента A(i) в точке H(j').

Расстояние l ( i , j ) между точками A ( i ) и H ( j ) равно

l(i, j) = 7L2 + d2(i - j)2 , тогда ф (i, j) - это дробная часть отношения l (i, j) к длине волны:

ф ( i , j) = { l ( i , j )/ X } .

Совокупность n точек H (j) образует простейшую линейную голограмму – голограмму точки. Таким образом, одномерному объекту A(i) ставится в соответствие одномерная голограмма H (j). Значения полученной голограммы округляются до одного бита – положительные принимаются за 1, отрицательные – за 0, в результате чего формируется n-битный одно- мерный массив HO (j), представляющий из себя кодовую комбинацию, соответствующую k-разрядному входному блоку данных X. Округление значений голограммы не вносит цифрового шума округления, так как информация заложена не в значениях точек (яркости) голограммы H (j), а в положении (номере позиции i = X) центра зон Френеля.

Таким образом, массив H O ( j ) – это голограмма точки, она же одномерная зонная линейка, несущая информацию о входном блоке данных в виде n-разрядного кода координаты центра зон Френеля.

Кодовая комбинация (кодовое слово) H O ( j ) передается по каналу связи с помехами и на приемной стороне производится декодирование – нахождение центра зон Френеля, определение его адреса и формирование k -разрядного выходного блока данных.

• 1.2.    Алгоритм декодирования

2.    Апробация голографического кодирования на имитационной модели

Принятая по каналу связи искаженная кодовая комбинация H R ( j ) рассматривается как одномерный массив точек, число которых может быть меньше n вследствие потери части информации, а значения принятых элементов искажены шумом. Каждая из n точек кодовой комбинации H R ( j ) является источником сферической волны с той же длиной волны λ, как и при кодировании. Восстанавливаемый объект A R ( i ) представляет собой одномерный массив точек, расположенных с шагом d на прямой, параллельной массиву H R ( j ), и находящейся на расстоянии L от него. Если каждая из n точек массива H R ( j) представлена одним битом, то объект A R ( i ) содержит n многоразрядных элементов, число бит в которых зависит от длины кодовой комбинации и введенной избыточности r = n – k .

Интенсивность волны от точки массива H R ( j ) в точке восстанавливаемого объекта A R ( i ) вычисляется так же, как и при кодировании (1). В каждую точку объекта A R ( i ) приходят волны от каждой точки H R ( j ) со своим значением фазы, и в результате интерференции этих волн формируются значения восстановленного объекта A R ( i ):

A r ( i ) = Z n = 1 H r ( j ) sin Ф ( i , j ), i = 1, ^, n. (2)

Таким образом, восстановленный объект A R ( i ) является голограммой второго порядка (голограммой голограммы) исходного объекта. С оптической точки зрения восстановленный объект представляет собой темную линию с одной яркой точкой и небольшой фоновой засветкой в остальных точках.

Для получения выходного блока данных в форме k-разрядного кода необходимо определить адрес яркой точки – номер позиции Y, в которой находится максимум массива AR (i). Этот номер и есть значение выходного блока данных XR. При искажении сигнала в процессе передачи (шумы, помехи, потеря части сигнала) отношение амплитуды пика к уровню шума в восстановленном сигнале снижается, и результат декодирования принимает вероятностный характер. При этом наличие любой ошибки в декодированном сигнале делает результат восстановления неприемлемым, поэтому основной характеристикой кода является вероятность получения безошибочного результата.

Оценка эффективности голографического кодирования в сравнении с существующими помехоустойчивыми кодами проведена путем моделирования в среде MATLAB процесса искажения и восстановления кодовой комбинации H O ( j ) при наличии случайных и пакетных ошибок.

Алгоритм моделирования:

• 1.    Кодирование:

• •    задается размер кодируемого блока k ,

• •    задается кодируемое значение X в диапазоне 1,…, n , где n =2 ^k ,

• •    формируется вторичный блок A ( i ), i = 1,…, n , содержащий одну единицу в позиции i = X , остальные – нули,

• •    вычисляется голограмма H ( j ) по формуле (1) и округляется до одного бита, в результате формируется однобитная последовательность H O ( j ), являющаяся кодовым словом для исходного значения X .

• 2.    Моделирование передачи по зашумленному каналу: с помощью встроенной в MATLAB функции awgn на сигнал H O ( j ) накладывается белый шум с заданным отношением сигнал / шум ( S / N ).

• 3.    Декодирование:

• •    вычисляется восстановленный объект A R ( i ) по формуле (2),

• •    находится максимум A R ( i ), его координата i = Y является выходным значением.

На рис. 1 показан результат кодирования (одномерная голограмма) 8-разрядного входного блока данных со значением X = 100, длина кодовой комбинации – 256 бит.

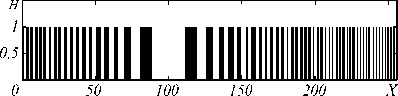
Рис. 1. Одномерная голограмма (последовательность нулей и единиц) в кодовом слове длиной n = 256

На рис. 2 приведен результат декодирования (восстановленное изображение объекта) A R ( i ) с ярко выраженным максимумом в позиции Y = 100. Декодирование производилось при наличии шума в канале, отношение сигнал / шум S / N =0 дБ. Шум в канале увеличивает паразитную засветку восстановленного объекта, при этом исправление ошибок происходит до тех пор, пока не появится шумовой выброс, превосходящий по величине информационный пик, и, соответственно, изменится координата максимума Y .

Исследование зависимости корректирующей способности голографического кода от расстояния между объектом и голограммой L , шага голограммы d и длины волны λ показало, что наилучшие результаты достигаются при значениях L = n d и λ = d .

Рассмотрим возможности кода по исправлению ошибок.

Корректирующие способности помехоустойчивого кода, имеющего n =2 ^k символов в кодовой комбинации, из которых k символов информационные, оцениваются максимальным количеством ошибок t , которые он может исправить при заданной степени избыточности. Например, для кода Рида–Маллера (РМ-код) t =2 ^{k – 2}–1 [9], что соответствует исправлению ошибок любого вида, составляющих до 25 % длины кодового слова.

н о nfy^ntty^m'iW^Ttntfrn^Z^^^TrZT^^TZ^

О 50       100      150      200        Y

Рис. 2. Результат декодирования при n = 256, уровень шума S / N = 0 дБ, декодированное значение Y = 100

Одним из самых эффективных из известных кодов для исправления ошибок является код Рида– Соломона (РС-код), широко применяемый в помехоустойчивом кодировании, в системах восстановления данных с компакт-дисков, при создании архивов с возможностью восстановления информации в случае повреждений [10]. Предел корректирующей способности ( n , k ) РС-кода определен границей Синглтона [11], в соответствии с которой для исправления t ошибок код должен иметь не менее n – k =2 t проверочных символов, т.е. два проверочных символа на одну ошибку. При большой степени избыточности ( n >>  k ) число исправляемых ошибок t приближается к 50% от длины кодового слова n . Например, РС-код (255,8) с коэффициентом избыточности 32 устраняет 123 ошибки, при этом в кодовом слове содержится 132 верных символа – ошибки занимают 48% кодового слова. Особенностью РС-кода является то, что столь высокую исправляющую способность он демонстрирует только для пакетных ошибок [10]. В то же время для большинства цифровых каналов, описываемых моделью двоичного симметричного канала без памяти, характерны случайные ошибки [10]. Если перейти от пакетных ошибок к равномерно распределенным по кодовому слову случайным ошибкам, максимальное число исправляемых РС-кодом ошибок составит t = n /2 k – 1. Отсюда следует, что тот же вариант ( n , k ) РС-кода при n = 256, k =8 исправляет 15 случайных ошибок, что составляет 6% длины кодового слова.

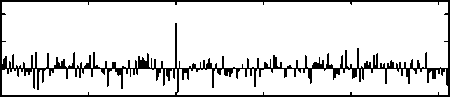
Голографический код обеспечивает высокую устойчивость как к случайным, так и к пакетным ошибкам. Для введения в кодовую комбинацию заданного числа случайных ошибок использовалась функция randperm (m, m), генерирущая m уникальных чисел в диапазоне от 1 до m. Эти числа использовались как адреса битов, в которые вносится ошибка. Результат восстановления искаженной кодовой комбинации длиной n =256, содержащей 80 случайных ошибок (искажен 31 % длины кодового слова), приведен на рис. 3. В результате проведения 100 000 испытаний установлено, что вероятность ошибки декодирования, т.е. вероятность неправильного определения положения информационного максимума при 80 ошибках составляет 0,00005.

н

О -20

О 50       100      150      200 Y

Рис. 3. Результат декодирования кодового слова, в котором 31 % случайных ошибок

Для оценки помехоустойчивости голографического кода проведено сравнение надежности передачи информации по каналу с аддитивным белым гауссовским шумом при использовании нескольких кодов. Рассмотрена зависимость вероятности ошибки декодирования от отношения сигнал / шум в канале для РС-кода, РМ-кода, мажоритарного кода и голографического кода. Для этого взяты рассмотренные выше предельные количества исправляемых ошибок для каждого кода и построена зависимость вероятности появления числа ошибок не больше предельного от отношения сигнал / шум. Во всех случаях число разрядов исходного слова – 8, длина кодового слова – 256 бит (скорость кодов R = 1/32). Результаты приведены на рис. 4.

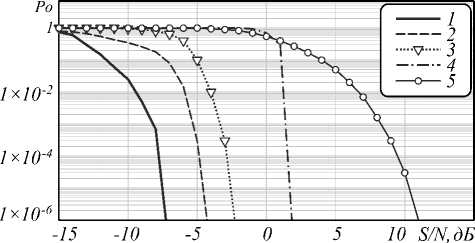
Рис. 4. Зависимость вероятности ошибки декодирования P o от отношения сигнал / шум при скорости кода R = 1/32: 1 – голографический код, 2 – мажоритарный код, 3 – РМ-код, 4 – РС-код, 5 – без кодирования

Одним из наиболее надежных способов передачи информации в сильно зашумленных каналах является усреднение в пределах введенной избыточности с мажоритарным способом выбора решения. Однако оказалось, что голографический код является более помехоустойчивым и обеспечивает выигрыш на 2 дБ по сравнению с мажоритарным кодом, что позволяет получить вероятность ошибки декодирования 10^-6 при отношении сигнал / шум S / N =–7 дБ.

Аддитивный шум существует в аналоговых каналах связи, а помехоустойчивое кодирование применяется для цифровых сигналов, в которых основной характеристикой качества канала является вероятность ошибки на бит (BER).

На рис. 5 показаны зависимости вероятности ошибки декодирования P O от вероятности ошибки в канале BER для тех же кодов, полученные расчетным путем для РС- и РМ-кодов, исходя из предельного количества исправляемых ошибок для каждого кода, и путем моделирования для мажоритарного и голографического кодов. При той же скорости кода R = 1/32 голографический код обеспечивает вероятность ошибки декодирования менее 10 ^{– 4} при вероятности ошибки в канале до уровня BER=0,34.

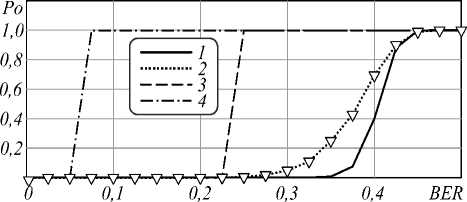
Рис. 5. Зависимость вероятности ошибки декодирования Po от вероятности ошибки на бит BER:

1 – голографический код, 2 – мажоритарный код, 3 – РМ-код, 4 – РС-код

Рассмотренные примеры искажения передаваемого сообщения характерны для двоичного симметричного канала без памяти – ошибки в нем являются независимыми. В то же время для большинства каналов радиосвязи (кроме космических каналов) характерно наличие эффекта замирания вследствие многолучевого распространения. К ним относятся каналы мобильной беспроводной связи, ионосферные и тропосферные каналы. В них искажения вызывают ошибки, имеющие вид пакетов, а не отдельных изолированных ошибок [10].

Сама по себе задача исправления ошибок во всех разрядах двоичного кодового слова является тривиальной – для этого достаточно инвертировать каждый разряд. Проблемой в этом случае для известных кодов является выбор из двух равновероятных результатов декодирования – прямого и инвертированного. Голографический код в отличие от других кодов дает совпадающий результат декодирования как для прямого, так и для инвертированного блока данных. На рис. 6 приведен результат декодирования блока с числом ошибок, равным 100 %. Как видно из сравнения с результатом декодирования неискаженного блока (рис. 2), пакетные ошибки приводят к инверсии вторичной голограммы и для восстановления значения входного блока данных необходимо лишь определить точку глобального экстремума независимо от его знака. Этот эффект можно объяснить также тем, что координаты центра зон Френеля вычисляются с одинаковым успехом для позитивного и негативного (100 % ошибок) изображения пластинки Френеля.

Более сложной задачей является восстановление блока данных, когда в кодовом слове содержится около 50 % группирующихся в пакет ошибок.

Решается эта задача следующим образом. Декодируемая кодовая комбинация разбивается на четыре равные части, и каждая часть обрабатывается в прямом и инвертированном виде. В оптической интерпретации – каждая четверть голограммы рассматривается как позитивное и негативное изображение, по каждому из которых происходит определение центра зон Френеля – восстановление исходного объекта (значения декодируемого блока данных). Это позволяет исправить все пакетные ошибки с размером пакета от 0 до 100% длины кодовой комбинации при любом расположении пакета в кодовом слове. Таким образом, предельные возможности РС-кода – исправление 50% пакетных ошибок, голографического кода – 100% ошибок.

н

о

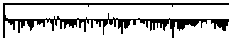
frf^rf^viiY^m^T'T^jr'

-50 -

-100 -о

50      100      150      200

Рис. 6. Результат декодирования при 100 % пакетных ошибок

Голографический код эффективен и при декодировании сигналов, содержащих смесь случайных и зависимых ошибок. При исследовании работы декодера в этом режиме ошибки в кодовую комбинацию вносились с помощью генератора случайных чисел. При числе ошибок менее 50% они являются случайными и при длине кодового слова n = 1024 вероятность ошибки декодирования P O = 0,001 при t =41 % ошибок (рис. 7).

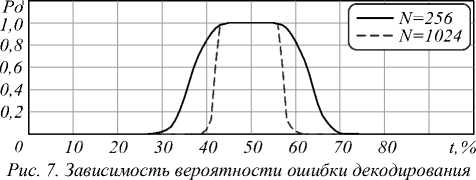
Po от числа ошибок t при длинах кода n = 256 и n = 1024

Максимальное возможное число независимых случайных ошибок в достаточно длинной кодовой комбинации составляет 50 % от количества бит в кодовом слове. При дальнейшем воздействии источника случайных ошибок происходит наложение ошибок и в итоге формируется случайное кодовое слово, половина бит которого совпадает с битами любого другого кодового слова. Для введения более 50% ошибок биты для искажения выбираются с учетом уже имеющихся ошибок, поэтому ошибки становятся зависимыми. При числе ошибок более 50 % результаты де- кодирования формируют правую часть графика зависимости вероятности ошибки декодирования PO от числа ошибок t (рис. 7). При общем числе ошибок более 60% добавляющиеся ошибки заполняют промежутки между случайными ошибками, превращая их в пакетные, что дает возможность провести полное восстановление информации. Таким образом, голографический код позволяет исправить смесь случайных и зависимых ошибок, если их общее число превышает 60% длины кодового слова.

Заключение

Голографический метод помехоустойчивого кодирования обеспечивает полное восстановление данных, содержащих до 40% случайных независимых ошибок и до 100% зависимых пакетных ошибок.

Другим преимуществом голографического кода является меньшая сложность кодирования и декодирования при изменении избыточности в широких пределах. Декодирование широко применяемого кода Рида–Соломона представляет собой довольно сложную задачу, для решения которой разработано несколько видов алгоритмов. Например, алгоритм Пи-терсона–Горенстейна–Цирлера сводит задачу нахождения позиций и значений t ошибок к решению двух систем линейных уравнений порядка t . Для решения можно воспользоваться методом Гаусса, и тогда сложность вычислений будет иметь порядок t ³ [9].

Декодирование голографического кода состоит в n ²-кратном вычислении A R ( i ) по формуле (4), что существенно проще алгоритмически и требует меньших вычислительных ресурсов.

Голографический код представляет интерес для передачи информации по каналам с низким отношением сигнал / шум (космическая связь или оптические системы связи, использующие свободное пространство в качестве канала передачи, наземная, в том числе мобильная радиосвязь, а также оптические системы связи на основе RoF технологии). Кроме того, он может повысить надежность хранения информации в системах, подверженных воздействию ионизирующего излучения (космическая техника) [12] и т.д.

Исследование выполнено за счет гранта Российского научного фонда (проект № 18-19-00123) в частях «Алгоритм декодирования» и «Апробация голографического кодирования на имитационной модели», а также Министерства науки и высшего образо- вания РФ в рамках выполнения работ по Государственному заданию ФГБОУ ВО УГАТУ # FEUE-2020-0007 по теме «Теоретические основы моделирования и семантического анализа процессов преобразования вихревых электромагнитных полей в инфо-коммуникационных системах» в части «Алгоритма кодирования».