Построение с помощью графов математической модели микроконтроллерной системы управления двигателя-маховика в режиме заданной скорости для высокодинамичных космических аппаратов

В качестве исполнительных органов систем ориентации и стабилизации различных космических аппаратов (КА) применяются двигатели-маховики (ДМ) [1]. С появлением радиационно-стойкой микроконтроллерной техники появились новые возможности в управлении ДМ, а, следовательно, и КА.

Отсутствие импортонезависимого ДМ, обладающего передовыми возможностями по сравнению с российскими и зарубежными аналогами, выявило необходимость в разработке нового поколения ДМ с цифровым микроконтроллерным управлением (рис. 1) на одном из лидирующих предприятий по созданию космической техники в Российской Федерации — АО «Корпорация «ВНИИЭМ» [2].

Рис. 1. Общий вид двигателя-маховика с цифровым управлением

Постановка задачи

Изменение скорости вращения махового колеса создает управляющий момент, воздействующий на КА, и до настоящего времени управление ДМ в изделиях АО «Корпорация «ВНИИЭМ» осуществлялось по заданному крутящему моменту (режим управления моментом). Ввод микроконтроллерного управления в схему ДМ обеспечивает возможность реализации режима высокоточной стабилизации скорости ротора, позволяющего бороться с различного рода моментами при стабилизации КА. Также появляется возможность осуществлять с пошаговым контролем [величина шага задается тактом общения с бортовым комплексом управления (БКУ) КА] изменение скорости вращения ДМ, необходимое для фактической оценки управляющего воздействия на КА. Такой режим позволяет обеспечивать ДМ стабильными техническими характеристиками, несмотря на возможную нелинейность передаточной функции и износ системы в течение всего времени эксплуатации.

Концепция создания цифрового микроконтроллерного управления нового поколения ДМ ориентирована на обеспечение характеристик ДМ как исполнительных органов системы ориентации и стабилизации высокодинамичного КА. Эта концепция подразумевает вращение КА вокруг центра масс на максимально высоких допустимых значениях управляющих моментов, создаваемых системой ДМ, и высокоточную стабилизацию данного вращения КА за кратчайшее время.

Для осуществления натурного моделирования [3] создан макет ДМ с цифровым микроконтроллерным управлением (ДМ-МК). За основу создания концептуальной модели взята аналоговая схема ДМ, разработанного и выпускаемого АО «Корпорацией «ВНИИЭМ» (ДМ20-250), маховичный электропривод которого выполнен на основе бесконтактного электродвигателя постоянного тока [4]. Цифровая схема управления реализована микроконтроллерным модулем (МКМ) [5]. Для организации обратной связи по скорости вращения ДМ-МК в схему электромеханического блока (ЭМБ) введен оптоэлектрический датчик скорости [6], информация с которого для дальнейшей обработки поступает в МКМ (рис. 2). Анализируя сигналы управления с БКУ КА и информационные сигналы с датчика скорости ЭМБ, МКМ формирует необходимое аналоговое управляющее напряжение ( U_c ), пропорционально которому ЭМБ создает крутящий момент на валу ДМ-МК.

По итогам успешной экспериментальной проверки макета ДМ-МК на работоспособность в стандартном режиме управления моментом сформулирована следующая научная задача [7]: Дано:

Основные технические характеристики ДМ-МК:

управляющий момент             1 Нм;

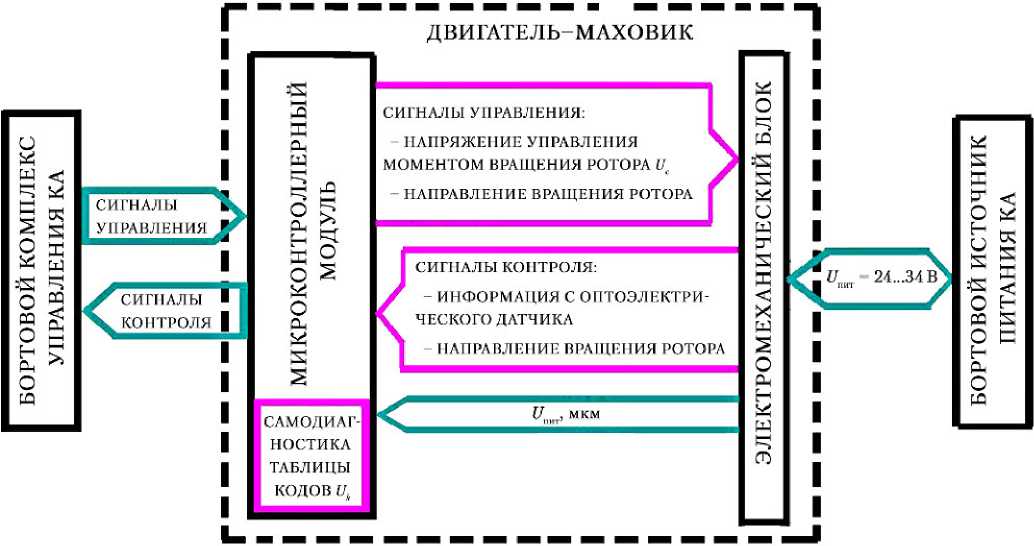
Рис. 2. Блок-схема двигателя-маховика с цифровым микроконтроллерным управлением

кинетический момент диапазон изменения частоты вращения максимальный потребляемый ток число импульсов на оборот масса напряжение питания тип семейства микроконтроллера такт общения с БКУ КА срок службы

Допустимое отклонение

±10 Нмс;

±1 300 об./мин;

10 А;

1 360;

8 кг;

24….34 В;

MCS -51;

125 мс;

не менее 12 лет. частоты вращения

ротора в режиме управления по скорости ДМ-МК:

– при неизменной заданной частоте — не более 1 об./мин;

– при темпе изменения заданной частоты не более 1 000 об./мин2 — не более 2 об./мин; – при темпе изменения заданной частоты вращения в диапазоне 1 000…8 000 об./мин2 — не более 10 об./мин.

Найти:

Функцию управления ДМ-МК в режиме заданной скорости.

Для поиска функции управления ДМ-МК в режиме заданной скорости необходимо проанализировать внутренние связи и воздействующие факторы (рис. 3). Отметим, что поиск осуществляется для всего рабочего диапазона скоростей вращения ротора, где величины паразитных моментов, наличие которых обусловлено различными факторами (в т. ч. моменты трения подшипников, изменяющиеся свойства смазок, термические процессы в конструкции и т. д.), для разных скоростей различны [8]. Поэтому в решаемой задаче необходимо учитывать нелинейность данной системы, обусловленную изменением электромеханических характеристик во время работы в течение всего срока жизни изделия.

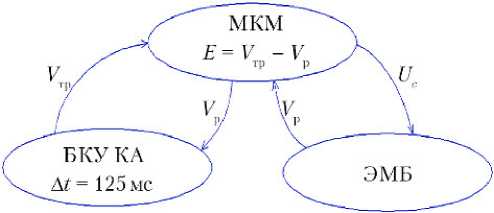
Рис. 3. Блок-схема причинно-следственных связей для построения графа: МКМ — микроконтроллерный модуль; БКУ КА — бортовой комплекс управления космического аппарата; ЭМБ — электромеханический блок; Е — ошибка скорости; V_тр — требуемая скорость вращения ротора ДМ; V_р — реальная скорость; U_c — управляющий сигнал

Построение математической модели с использованием графов для решения научной задачи

При построении математической модели были проанализированы различные варианты математического исследования поставленной задачи [9–11]. В результате проведенного анализа было предложено одно из возможных направлений исследования ДМ-МК как системы с помощью системного анализа, базирующегося на теории отношений и графов. Отметим, что использование теории графов в построении математической модели ориентируется на концепцию разработки высокодинамичного КА.

Концепция построения графа базируется на поиске быстрейшего выхода и стабилизации значения требуемой скорости ( V _тр) вращения ротора ДМ. Разница между V _тр и реальной ( V _р) скоростями вращения ротора ДМ определяет значение ошибки скорости ( Е ). Задача сводится к формированию микроконтроллерным модулем управляющего сигнала U _c с целью достижения и обеспечения нулевого значения Е ( E ₀). Отметим, что отклонение частоты вращения ротора в режиме управления по скорости ДМ-МК допустимо в пределах требований к ДМ.

Построим ориентированный граф (рис. 4) [12], где вершинами являются значения Е ; веса дуг определяются значениями U _с, вычисленными с учетом снятых с ДМ-МК и контролируемых значений напряжения компенсации момента трения U_k для всего диапазона скоростей вращения ротора; длительность времени Δ t между соседними вершинами, объединенными дугами, соответствует времени обновления информации о скорости вращения ротора (см. разд. «Постановка задачи»).

Граф построен от возможного начального значения Е ( Es ), где Еs (рис. 4, вершина а ) может быть от 0 до 2 600 (см. разд. «Постановка задачи», диапазон изменения частоты вращения) до E 0. На графе представлен случай, где Δ E_m — максимальное значение Е за Δ t , возможное при формировании МКМ максимального значения U_c ( U_m ), согласно техническим характеристикам ДМ-МК Δ E_m = 20. В случае, если Es ≤ Δ E_m , Еs принимает значение вершины, соответствующей значению Е в диапазоне Е 0… Е 20 (рис. 4).

Отметим, что учет значений U_k имеет большое значение в расчете U_c , так как в течение срока жизни изделия U_k может достигнуть значений, близких к 50% U_m . Таким образом, в случае варианта увеличения значения скорости вращения ротора ДМ момент трения может привести к останову набора скорости вращения ротора (рис. 4, вершины а–b 1), так как U_с станет равным U_k .

Снижение значения U_с для уменьшения Δ E_m (с целью повышения вероятности попадания в требуемую скорость) ведет к неблагоприятному замедлению функции управления за счет появления дополнительных тактов Δ t (рис. 4, сравните варианты вершины точного выхода на Е 0: вершины a–с 21 с вершинами а–у 2). Поэтому, руководствуясь концепцией построения графа для быстрейшего выхода на требуемую скорость, целесообразно до момента определения Е в зоне Δ E_m (т. е. Е ≤ E_m ) управление осуществлять на значении U_c = U_m (рис. 4, см. дугу a–z 1).

По результатам математической оценки (в т. ч. с помощью метода Монте-Карло), в связи с тем, что рассматриваемое значение Es носит стохастический характер, вероятность точного попадания (рис. 4, вариант вершин a–zn) в значение E0 определяется величиной значения ΔEm и, соответственно, составляет 5%. Отметим, что величина значения ΔEm может изменяться в течение срока жизни изделия, поэтому в программное обеспечение МКМ введен корректирующий коэффициент ΔEm, но в данной статье фактор старения системы не учитывается.

На графе рис. 4 представлены все варианты вершин с соответствующими дугами, обеспечивающие точный выход на значение Е 0, без перерегулирования c момента определения Е в зоне Δ E_m . Отметим, что варианты с перерегулированием не рассматриваются, так как при перерегулировании за 1 Δ t (100 мс) вероятность точного выхода на V _тр определяется «плавающей» задержкой отработки управляющего воздействия U_c , которая носит стохастический характер и может иметь разную длительность — от 1 до 60 мс. Данная задержка обусловлена переходными процессами механической и электрической составляющих ЭМБ, приводящих к необходимости наличия «затухающего» перерегулирования, стремящегося к Е = 0 (см. рис. 4, дуги z 1– zn ). Таким образом, появляются дополнительные затраты времени как следствие устранения низкой точности выхода на требуемую скорость, неблагоприятные для решаемой задачи.

Для характеризации построенного графа (рис. 4) строим матрицу инцидентности ( М_i ) [13], где «0» — вершина графа не инцидентна дуге графа; «1» — дуга выходит из вершины; «–1» — дуга входит в вершину (табл. 1).

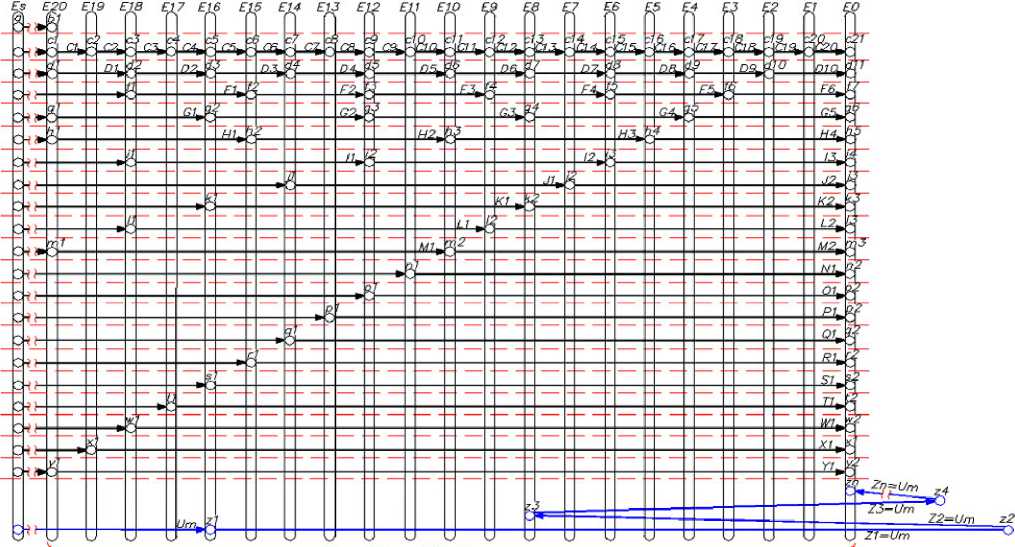
Зона EgEm для' Uc=Um

Рис. 4. Функциональный ориентированный граф отработки новой требуемой скорости

Таблица 1

Вершины графа E20 E19 E18 E17 E16 E15 E14 E13 E12 E11 E10 E9 E8 E7 E6 E5 E4 E3 E2 E1 E0 Он S ч C1 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C2 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C3 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C4 0 0 0 1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C5 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C6 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C7 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 C8 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 0 C9 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 0 C10 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 0 0 C11 0 0 0 0 0 0 0 0 0 1 1 –1 0 0 0 0 0 0 0 0 0 C12 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 0 C13 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 0 C14 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 0 C15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 0 C16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 0 C17 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 0 C18 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 0 C19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 0 C20 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 –1 D1 1 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 D2 0 0 1 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 D3 0 0 0 0 1 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 D4 0 0 0 0 0 0 1 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 D5 0 0 0 0 0 0 0 0 1 0 –1 0 0 0 0 0 0 0 0 0 0 D6 0 0 0 0 0 0 0 0 0 0 1 0 –1 0 0 0 0 0 0 0 0 D7 0 0 0 0 0 0 0 0 0 0 0 0 1 0 –1 0 0 0 0 0 0 D8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 –1 0 0 0 0 D9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 –1 0 0 D10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 –1 F1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 F2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 F3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 F4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 F5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 F6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 G1 1 0 0 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 G2 0 0 0 0 1 0 0 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 G3 0 0 0 0 0 0 0 0 1 0 0 0 –1 0 0 0 0 0 0 0 0 G4 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 –1 0 0 0 0 G5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 –1 H1 1 0 0 0 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 H2 0 0 0 0 0 1 0 0 0 0 –1 0 0 0 0 0 0 0 0 0 0 H3 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 –1 0 0 0 0 0 H4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 –1 I1 0 0 1 0 0 0 0 0 –1 0 0 0 0 0 0 0 0 0 0 0 0 I2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 –1 0 0 0 0 0 0 I3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 –1 J1 0 0 0 0 0 0 1 0 0 0 0 0 0 –1 0 0 0 0 0 0 0 J2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 –1 K1 0 0 0 0 1 0 0 0 0 0 0 0 –1 0 0 0 0 0 0 0 0 K2 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 –1 L1 0 0 1 0 0 0 0 0 0 0 0 –1 0 0 0 0 0 0 0 0 0 L2 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 –1 M1 1 0 0 0 0 0 0 0 0 0 –1 0 0 0 0 0 0 0 0 0 0 M2 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 –1 N1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 –1 O1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 –1 P1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 –1 Q1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 R1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 S1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 T1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 W1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 X1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 Y1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 Z1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 матрица инцидентности Мi зоны Е ≤ ΔEm

В данной матрице М_i в качестве примера результата отработки Es (рис. 4, вершины а–z 1) на значении U_c = U_m обозначена синим цветом зона Е 16, из которой желтым цветом выделены возможные ориентированные маршруты (их длины выражены дугами C5– C 20; D 3– D 10; G 2– G 5; K 1– K 2; S 1), приводящие из Е 16 точно в Е 0.

Для поиска наименьшей длины пути возможных ориентированных маршрутов построим матрицы смежности ( M_{c 0}, M_{c 1}, M_{c 2}, M_{c 3}, M_{c 4}), для удобства и наглядности наложим их друг на друга, цветом выделим соответствующие связи вершин (обозначенные «1») в рамках каждой матрицы (табл. 2).

Найдем степенную матрицу M_c^L с помощью последовательного умножения матриц смежности возможных ориентированных маршрутов M_{c 0}; M_{c 1}; M_{c 2}; M_{c 3}; M c 4 (т. е. M c = M 0 X M c 1 X M c2 X M c3 X M c4 ) Результат последовательного умножения данных матриц высчитывается по правилам конъюнкции булевой алгебры

(при перемножении наличие «1» в столбце матрицы, участвующей в вычислении, обозначает требование игнорирования наличия нулей как потенциальных вариантов связи в данной матрице с данной вершиной). В результате последовательного умножения получено следующее свойство элементов маршрута поиска x_ij степенной матрицы M^ x x^L ^ = 1, которое означает, что существуют один или более ориентированных маршрутов длиной x_ij из x_i в x_j , так как выполняется следующее условие:

V(k < L)(xj) = 0) Л (xj) = 1), где k — опознавательный индекс степенной матрицы Mck, являющейся последовательным произведением Mc = Mc0 x Mc 1 x Mc2 x Mc3 и не содержащей ориентированных маршрутов наименьшей длины xij из xi в xj, матрица McL содержит маршрут наименьшей длины xij, являющийся решением данного примера, и соответствует вершинам s1–s2 функционального ориентированного графа отработки новой требуемой скорости (см. рис. 4).

наложение матриц смежности

Таблица 2

	Вершины графа
	х i																х j
	E 16	E 15	E 14	E 13	E 12	E 11	E 10	E 9	E 8	E 7	E 6	E 5	E 4	E 3	E 2	E 1	E 0
E 16	0	1	1	0	1	0	0	0	1	0	0	0	0	0	0	0	1
E 15	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
E 14	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0
E 13	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0
E 12	0	0	0	0	0	1	1	0	1	0	0	0	0	0	0	0	0
E 11	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0
E 10	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0
E 9	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0
E 8	0	0	0	0	0	0	0	0	0	1	1	0	1	0	0	0	1
E 7	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0
E 6	0	0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0
E 5	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0
E 4	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	0	1
E 3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0
E 2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1
E 1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1
E 0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Примечание. H — M c ₀ ; H — M c 1 ; H — M c ₂ ; H — M c ₃ ; H — M c ₄ .

заключение

По итогам проделанной работы с помощью графов выполнена задача поиска функции управления ДМ в режиме заданной скорости вращения ротора для высокодинамичных КА, и построена математическая модель поиска функции управления в реальном масштабе времени. Найденная функция управления ДМ была интегрирована в программное обеспечение МКМ. Натурные испытания, проведенные на макете ДМ-МК, подтвердили выполнение решаемой задачи и требований к допустимому отклонению частоты вращения ротора в режиме управления по скорости ДМ-МК (рис. 5).

Внедрение ДМ-МК с реализованным режимом управления по скорости осуществляется в настоящее время.

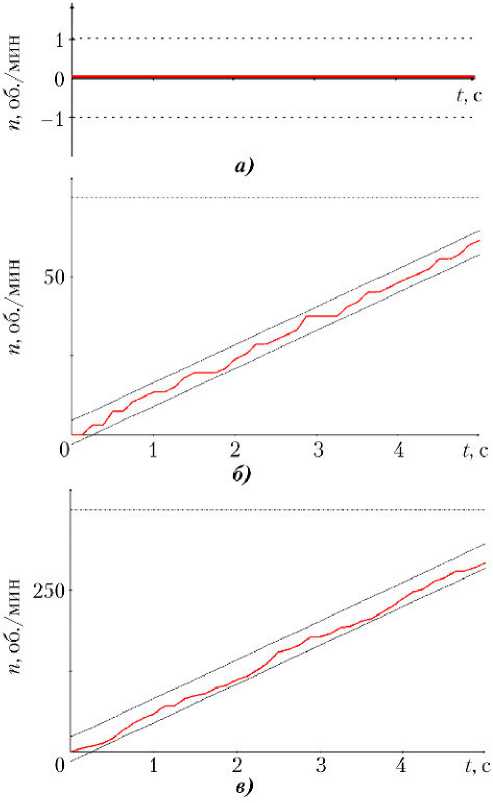
Рис. 5 Соответствие допуску отклонения частоты вращения ротора в режиме управления по скорости ДМ-МК: а — при неизменной заданной частоте — не более 1 об./мин (в примере V_тр = 500 об./мин); б — при темпе изменения заданной частоты не более 1 000 об./мин² — не более 2 об./мин; в — при темпе изменения заданной частоты вращения в диапазоне 1 000…8 000 об./мин² — не более 10 об./мин

Автор выражает благодарность сотрудникам АО «Корпорация «ВНИИЭМ»: дтн Макриденко Л.А., дтн Сарычеву А.П., ктн Рогозе А.В., Медушеву С.В., Щетинину М.Ю., ктн Кузьмину В.К., Городецкому Р.С., Кубраку В.К., Медушеву А.С., Соколунину И.В. за обеспечение возможности создания и отработки цифрового микроконтроллерного управления на образцах двигателей-маховиков, разработанных и выпускаемых АО «Корпорация «ВНИИЭМ».

Отдельную признательность автор выражает дтн Бабишину Владимиру Денисовичу за руководство по созданию диссертационной работы, в рамках которой написана данная статья.