Построение управляемых комплексов OLAP-моделей

На сегодняшний день существует достаточно большое количество программных продуктов, реализующих функции OLAP-анализа. Такие крупные компании, как Hyperion Solutions Corp., IBM, Oracle, Microsoft, Sybase, Panorama Software, Cognos Inc. и другие ведут разработки в этой области, их решения охватывают практически все существующие задачи. Однако традиционные OLAP-решения малоэффективны в прикладных областях организационного управления, где необходим комплексный анализ данных, связанный с реализацией сложных аналитических алгоритмов. Методы расчета аналитических показателей для решения задач оперативного управления и планирования в здравоохранении, образовании, в сфере социальной защиты населения и множестве других прикладных областей представляют собой сложные многошаговые процессы анализа многомерных данных. Потребовался новый подход в OLAP-технологии, ориентированный на решение сложных аналитических задач, использующих связные многошаговые расчеты с множеством информационных объектов.

В статье представлены результаты работ по развитию функциональности OLAP-продуктов в рамках нового подхода, названного комплексным OLAP-моделированием [1; 2]. Описаны средства автоматизации разработки OLAP-приложений для сложных аналитических задач на основе построения управляемых комплексов OLAP-моделей.

Метаописание комплекса OLAP-моделей для сложных задач. Идея технологии OLAP хорошо описана [3–5]. В основе OLAP лежит многомерная логическая модель данных [6]. OLAP-модель (далее – модель) представляет собой описание процессов расчета некоторой аналитической задачи. Структурно аналитическая модель состоит из исходных данных (витрины данных), информационного куба и операций над ним, а также способов представления результатов вычисления.

Для решения сложных аналитических задач обычно строится не одна модель, а целый комплекс OLAP-моделей, каждая из которых решает отдельную подзадачу. Например, чтобы применить эту технологию к задаче планирования медицинской помощи, требуется построить модели анализа и прогноза демографической ситуации в регионе, анализа заболеваемости, анализа соответствия необходимых объемов медицинской помощи возможностям существующих медицинских учреждений и т. п. Каждая из перечисленных подзадач имеет самостоятельное значение, однако чтобы осуществить ежегодное планирование медицинской помощи в регионе, необходимо выполнить целенаправленный связный расчет с применением всего комплекса моделей. Для этого помимо средств сохранения результатов расчетов каждой модели необходимо обеспечить управление расчетами в зависимости от состояния задачи.

Построение управляемых комплексов OLAP-моделей для сложных аналитических задач предлагается осуще- ствлять на основе метаописания, которое включает в себя описание каждой модели, множество отношений между моделями, условия применения и коррекции моделей, условия альтернативного выбора модели. Метаописание комплекса OLAP-моделей осуществляется с применением специальной гибридной модели знаний декларативно-процедурного типа:

U=, где W = {M1, M2, ..., Мп} - описание множества моделей; R - отношения между моделями; U - условия применения и коррекции моделей.

Каждая OLAP-модель M е W представляется в виде M= < X , G , Q ( G ), S ( G )> .

Используются следующие обозначения:

X - дискретное множество входных данных модели (витрина данных);

G = < Z , F> - гиперкуб - модель логического многомерного представления данных, характеризующаяся двумя наборами параметров: показателями Z = < z _р z ₂, _, z m > и измерениями F = 1, f₂, ^,f>. Каждый показатель представляет собой множество значений, количественно характеризующих анализируемый процесс. Каждое измерение представляет собой упорядоченное множество значений определенного типа. Множество измерений образует оси гиперкуба. Измерения могут быть организованы в виде упорядоченной иерархической структуры;

Q ( G ) - функции, или процедуры, описывающие построение элементов гиперкуба G : показателей Z и измерений F , исходя из множества входных данных Х, а также операции над гиперкубом: агрегирование гиперкуба по иерархии атрибутов выбранного измерения, срез гиперкуба G по одному или нескольким заданным измерениям, операции поворота гиперкуба, изменяющие порядок измерений в гиперкубе;

S ( G ) - описание результатов вычисления OLAP-модели, обычно сохраняемых в виде таблиц агрегатов. Особенностью технологии OLAP является возможность наглядной визуализации результатов обработки в виде таблиц, кросс-таблиц, диаграмм, а также динамических картограмм [2].

Для описания моделей в работе [7] предложен специальный язык и разработаны программные средства генерации в этом языке скрипта OLAP-модели, который генерируется в результате ее интерактивного формирования в программной системе. Однако работать со скриптовым представлением оказалось довольно сложно, поскольку комплекс может содержать большое число моделей. К примеру, для задачи ежегодного планирования медицинской помощи комплекс включает более сорока OLAP-моделей.

Для повышения обозримости комплекса нами введено краткое метаописание OLAP-модели М в виде кортежа:

М : < витрина данных >; < назначение модели >;

< результат >.

Метаописание каждой модели М в базе знаний формируется автоматически, с помощью специально разработанного программного обеспечения на основе скрипта.

Для реализации управляемых расчетов, помимо описания отдельных моделей, необходимо описать их взаи- мосвязи. Это осуществляется путем описания отношений между моделями и условий их применения.

Основной вид отношений между моделями - отношение информационной зависимости моделей M _t ^ M 2 , которое определяет необходимость предварительного расчета модели M 1 для последующего расчета модели M ₂ . Обычно это отношение имеет место, если результаты вычисления M 1 используются как исходные данные для M ₂. Отношение информационной зависимости применяется для построения упорядоченных цепочек расчета OLAP-моделей. Можно также использовать отношение альтернативного выбора модели для случая, когда разные модели решают одну и ту же задачу разными методами.

Условия применения моделей описываются с помощью правил следующего вида:

R,: ЕСЛИP(х„х2, ...,Хп) ТО ВЫПОЛНИТЬ М/ ИЗМЕНИТЬ М, где Rj - уникальное в базе знаний имя правила; хр х2,^, хп - показатели, заданные как результаты расчета какой-либо модели, либо заданные в витрине как исходные данные. Каждый показатель представляет собой многомерный куб, описанный в витрине данных соответствующей OLAP-модели. Предикат P задается в виде логико-лингвистического выражения. Операция ВЫПОЛНИТЬ М в правой части правила R1 интерпретируется как выполнение расчета OLAP-модели М. Если в процессе логического вывода правило R2 применяется, то это приводит к расчету показателей - результатов модели М. Как следствие, должны быть пересчитаны все информационно зависимые OLAP-модели. Операция ИЗМЕНИТЬ М в правой части правила интерпретируется как переход к интерактивному процессу коррекции модели M. Пример правил такого типа приведен ниже.

Алгоритмы управления аналитическим расчетом. Метаописание комплекса OLAP-моделей используется в управляемых расчетах следующим образом. Генерация цепочек OLAP-моделей выполняется на основе их метаописания как процедура логического вывода на гибридной базе знаний. Процедура вывода представляет собой интерактивный процесс, позволяющий производить многовариантный расчет сложных многоэтапных задач.

Управление процессом расчета осуществляется на основе применения правил выполнения и выбора OLAP-моделей, а также с учетом действий пользователя. Пользователь может интерактивно изменить или заменить любую модель, вследствие чего изменяется ее системное представление. Также пользователь может изменить условия применения, изменив метаописание в базе знаний. Процедура логического вывода учитывает оба варианта. При этом автоматически исследуются возможные изменения расчета и строятся новые цепочки моделей. Кроме того, продукционные правила позволяют не только указывать условия применения моделей, но и в явном виде задавать в базе знаний такие важные элементы, как критерии согласованности показателей.

Рассмотрим алгоритм логического вывода, позволяющий выполнять управляемый многовариантный расчет на примере расчета Территориальной программы государственных гарантий оказания населению бесплатной медицинской помощи (далее - ТПГГ) с применением метаописания комплекса OLAP-моделей [8].

Чтобы выполнить процесс генерации цепочек OLAP-моделей, позволяющих рассчитать показатели объемов медицинской помощи и нормативы требуемого финансирования, а также выполнить согласование этих показателей, применяется по стро енное метаопис ание комплекса моделей. Генерация цепочек OLAP-моделей для расчета ТПГГ выполняется как интерактивный процесс логического вывода, позволяющий производить много- вариантный расчет ТПГГ либо в целом, либо отдельных ее фрагментов. Управление процессом расчета выполняется на основе применения правил выполнения и выбора OLAP-моделей, а также с учетом действий пользователя.

Рассмотрим алгоритм расчета с применением обратной цепочки вывода на базе знаний, представляющей метаописание комплекса моделей (рис. 1). Алгоритм условно можно разделить на три этапа: формирование цепочек OLAP-моделей, генерация скрипта цепочек и сам процесс расчета.

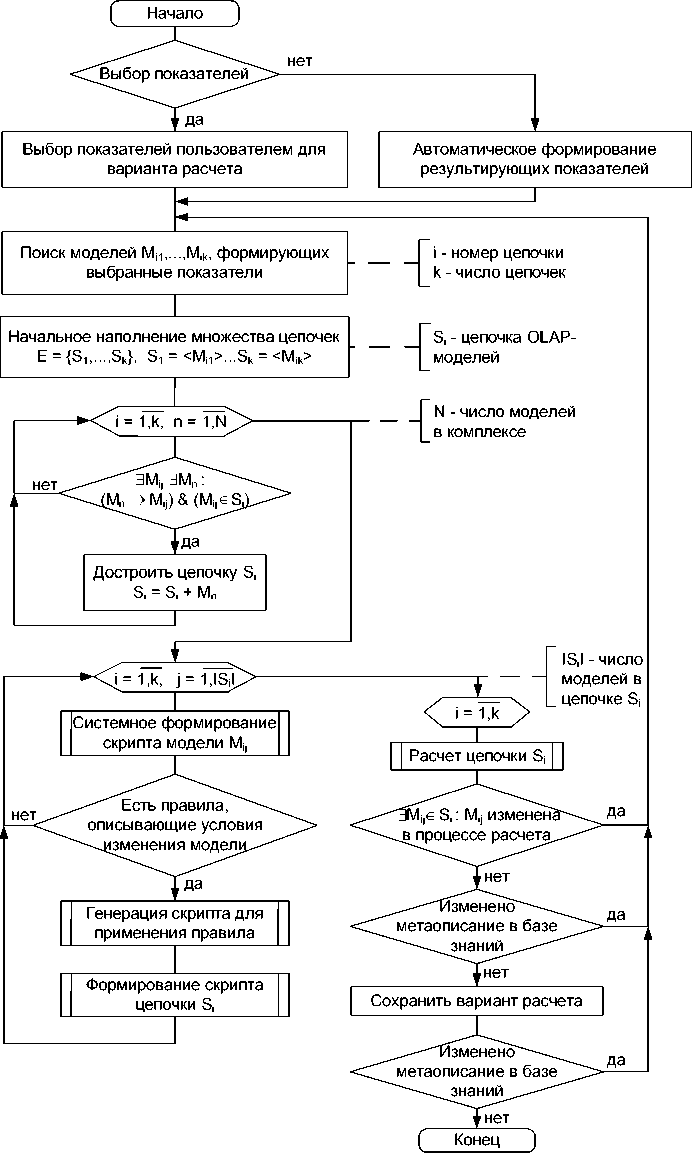
Рис. 1. Алгоритм расчета выбранных показателей

Построение цепочек предполагает определение зависимых моделей. Задаются показатели, которые необходимо рассчитать. Автоматически определяются необходимые для этого модели и порядок расчета. По описанию в базе знаний находятся модели такие, от которых информационно зависит какая-либо модель из числа помещенных в цепочки. Соответствующие цепочки дополняются.

Результирующие цепочки должны удовлетворять следующему требованию: любая зависимая модель должна располагаться в цепочке не раньше любой модели, от которой она информационно зависит; для каждой пары моделей в цепочке, если имеет место отношение М ₁ → М ₂, то М ₁ должна предшествовать М ₂ в цепочке. Это требование обеспечивает корректность расчетов.

Затем формируется скрипт построенных цепочек моделей (рис. 2). Для этой цели используется системное описание моделей и правила выполнения и выбора моделей, представленные в базе знаний. В зависимости от вида правил формируются и вставляются в скрипт цепочек управляющие элементы.

Полученный вариант расчета ТПГГ можно сохранить, затем изменить методику расчета, изменив модели или условия выполнения моделей, и вновь выполнить расчет.

Таким образом, можно получить несколько вариантов расчета ТПГГ и выбрать из них наиболее рациональный.

Многовариантный расчет можно выполнить также для того, чтобы применить разные модели балансировки показателей ТПГГ. Уточнение и балансировка показателей необходимы для согласования требуемых объемов медицинской помощи и выделенного финансирования. Можно изменить порядок расчета моделей балансировки, изменив в базе знаний приоритеты правил применения этих моделей.

В случае если в результате интерпретации правила R_i , описывающего в базе знаний условия выполнения, или изменения OLAP-модели, или отдельного показателя, оказалось, что левая часть правила – условие – оказалось выполнено, то в скрипт расчетной цепочки, куда помещена модель в результате выполнения предыдущего алгоритма, добавляется скрипт, позволяющий инициировать соответствующее действие. При этом, если в результате интерактивного взаимодействия с пользователем модель изменяется, то по алгоритму (см. рис. 1), это приводит к возврату к построению последовательности расчета заново.

Рассмотрим алгоритм проверки условия правила, содержащего многомерные показатели (рис. 3). Алгоритм записывается следующим образом:

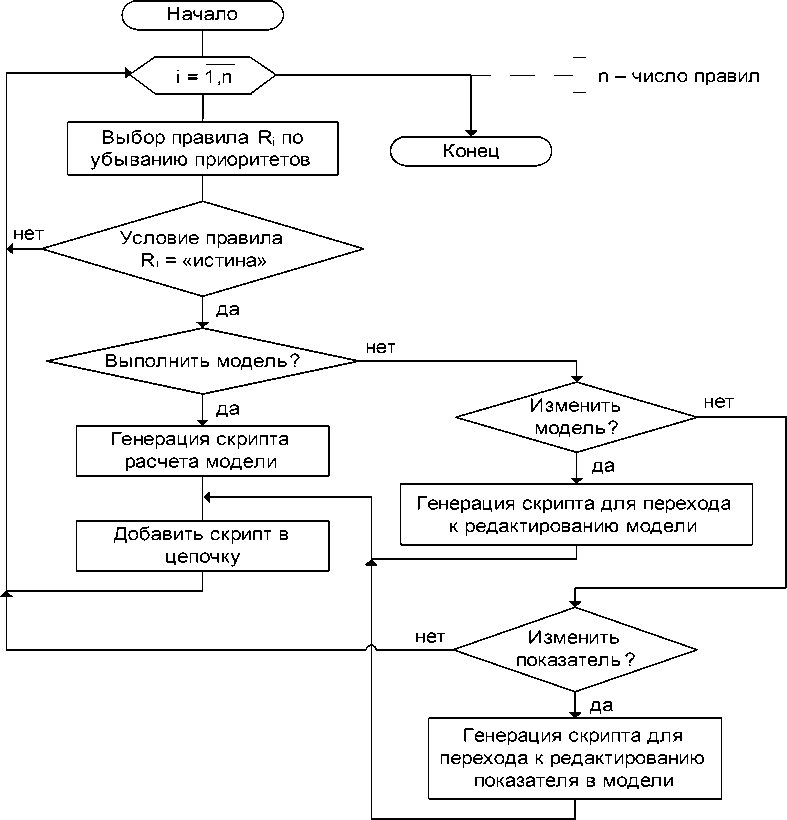
Рис. 2. Алгоритм формирования управляющих элементов в цепочке моделей

R ₁: ЕСЛИ ( х ₁ ~ a ₁) И ( х ₂ ~ a ₂) И … И ( х_n ~ a_n ) ТО ВЫПОЛНИТЬ М .

Суть алгоритма состоит в том, чтобы сравниваемые многомерные показатели привести к одинаковой размерности. Для этого по несовпадающим измерениям производятся срезы. Затем значения показателей, имеющие одинаковое положение в построенном кубе, попарно сравниваются, если отношение выполняется для всех пар, то условие правила истинно, в противном случае – условие ложно. Если показатели не имеют общих измерений, условие ложно.

Таким образом, рассмотренные алгоритмы позволяют выполнять расчет показателей путем реализации обратной стратегии логического вывода на знаниях, представляющих метаописание комплекса моделей.

Пример сводного расчета объемов медицинской помощи по круглосуточным стационарам представлен на рис. 4.

Таким образом, предложенный способ метаописания связных комплексов OLAP-моделей, основанный на декларативно-процедурной модели знаний, позволяет осуществлять управление многовариантными аналитическими расчетами путем построения упорядоченных цепочек OLAP-моделей. Особенностью является возможность применения многомерных условий в правилах, описывающих порядок вычисления моделей. Представленные алгоритмы управления аналитическим расчетом в комплексе применены для расчета показателей территориальной программы бесплатной медицинской помощи. Выполнена программная реализация полученных результатов. Программное обеспечение внедрено в агентстве здравоохранения Красноярского края.