Построение увеличенного изображения со сверхразрешением с помощью планарных ЛМ

Одной из важнейших характеристик любой изображающей оптической системы является оптическое увеличение, показывающее соотношение между размерами предмета и сформированного изображения данного предмета. Традиционно в геометрической теории изображений используют три вида увеличений – линейное (часто называют поперечным), угловое (называют также коэффициентом сходимости) и продольное [1, раздел 4.3.1]. Данная работа посвящена градиентным элементам микрооптики, строящим изображение с линейным увеличением и при этом обладающим сверхразрешающей способностью, заключающейся в разделимости изображений двух источников, разделённых расстоянием меньше половины длины волны света в вакууме.

Достижение такого сверхразрешения стало возможным в последние годы с развитием нанофотоники. В частности, это возможно с помощью суперлинз [2], представляющих собой, например, чередующиеся слои металла и диэлектрика. Эксперименты по сверхразрешению с помощью таких линз были осуществлены в [3, 4]. В [3] было достигнуто сверхразрешение, равное 0,4 λ , где λ – длина волны. Аналогичный эксперимент был проведён в [5] с помощью субволнового слоя серебра, который также работает как суперлинза. В этой работе были разрешены две линии, разделённые расстоянием 145 нм при освещении их ультрафиолетовым светом с длиной волны 365 нм. То есть в [5] было также достигнуто сверхразрешение, равное 0,4λ. В упомянутых работах использованы оптические элементы, включающие в себя металлические компоненты, проходя через которые свет будет поглощаться. В работах авторов [6, 7] рассмотрены градиентные элементы для построения изображения со сверхразрешением. Эти элементы полностью диэлектрические и не поглощают свет, но линейное увеличение в этих системах равнялось единице, т.е. формируемое изображение оставалось субволновым.

В работе [8] рассмотрена гиперлинза, строящая увеличенное изображение. Численно показано, что с помощью гиперлинзы, состоящей из 160 чередующихся 10-нанометровых слоёв из серебра (при λ=365 нм) и диэлектрика ( ε ≈ 2,7), можно сформировать увеличенное (примерно в 5 раз) изображение двух источников, разделённых расстоянием λ /4,5. Однако эта гиперлинза также включает в себя металл, и, хотя в работе [8] написано, что поглощение света несущественно, количественные данные о потерях не приводятся. Кроме того, источник света должен быть помещён внутрь цилиндрической гиперлинзы, т.е. в цилиндрическую полость, диаметр которой не указан, но, судя по рисункам в [8], примерно равен 200 нм. Это представляется непростой технической задачей.

В данной работе рассматривается построение увеличенного изображения с помощью линз Микаэляна (ЛМ) [9], состоящих полностью из диэлектриков. С использованием принципа Ферма предсказано положение изображения внеосевого источника, формируемого двумя кремниевыми ЛМ, расположенными вплотную друг к другу. Кремний для длины волны λ > 1 мкм почти не поглощает свет. Показано, что в оптической системе из двух ЛМ, одна из которых вдвое больше другой, изображение, формируемое внеосевым точечным источником, расположенным на расстоянии y от оптической оси, не находится на расстоянии, вдвое большем от оптической оси (т.е. 2 y ), а представляет собой световое пятно, основная энергия которого заключена в пределах (3,7 y ; 2 y ). Построение изображения с помощью двух линз и с помощью одной линейно расширяющейся ЛМ исследовано численно с помощью конечно-разностного FDTD-метода. Для системы двух ЛМ, одна из которых в 2,5 раза больше другой, получено изображение двух точечных источников света с линейным увеличением, равным 2,1. Для линейно расширяющейся ЛМ получено линейное увеличение 3,14. В обоих случаях были разрешены точечные источники, разделённые расстоянием 0,28 λ .

1. Уравнение траектории луча в градиентном волноводе

Пусть дан планарный градиентный волновод с оптической осью x и зависимостью показателя преломления от поперечной координаты n ( y ). Пусть луч света соединяет точки A и B с координатами

n(y ) =

n ₀

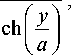
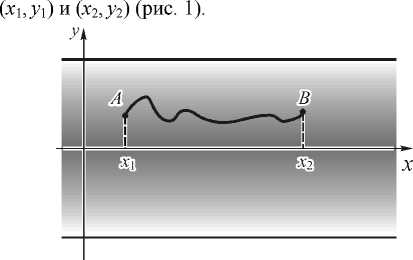
Рис. 1. Однородный градиентный волновод и световой луч, соединяющий две произвольные точки A и B

где n 0 – показатель преломления на оси волновода (т.е. при y =0), a – параметр, определяющий ширину волновода и задающий скорость спада показателя

преломления от оси волновода к его краям.

Подставив это выражение в уравнение для траектории луча (4), получим:

x ( y ) = D ± a arcsin

sh ( Z IV a )

7 n 2 C -1

Согласно принципу Ферма, световой луч проходит по траектории y ( x ), обеспечивающей минимальный оптической путь, т.е. минимум следующего функционала:

L [ y(x )] = f n(y)

x ₁

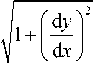
d x .

Известно, что такие задачи можно решать с помощью уравнения Эйлера–Лагранжа [10], которое для функционала (1) выглядит следующим образом:

Из полученного уравнения выразим явно sh ( y / a ) через x :

sh f ^y | = 7 n 2 C - 1 sin f x — D | .                (7)

V a)              к a )

Знак «±» в (7) опущен, так как изменение «+» на «-» достигается прибавлением n a к константе D . Обозначим ( n 2 C - 1 )^/ cos ( D/a ) как C , а ( n ₀ ² C - 1 )^Z sin ( D/a ) как - D . Тогда уравнение траектории луча в градиентном секансном волноводе примет вид:

sh ^{f y} | = C sin ^f x | + D cos ^f x | .                 (8)

V a ) V a ) V a )

1 d n = y"

n ( У ) ^d У 1 + ( y ' ) ² "

Умножив обе части на 2 y ΄ и проинтегрировав по переменной x , получим выражение для производной траектории луча y ( x ):

Пусть в плоскости x = x 1 луч проходит через точку с координатами ( x 1 , y 1 ) и тангенс угла наклона луча к оптической оси равен а (рис. 2).

d x =± 7 Cn ² ( ^{y )-} 1,

где C – постоянная.

Данное дифференциальное уравнение решается в радикалах, если искать траекторию луча через обратную функцию x ( y ):

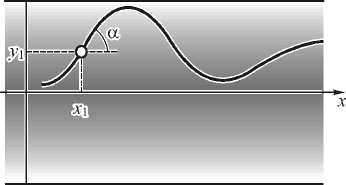
Рис. 2. Задание луча, распространяющегося в градиентном гиперболическом секансном волноводе, расстоянием от оптической оси y₁ и углом наклона к ней а в некоторой опорной плоскости x = x 1

y

x(y ) = ±J

d t

7Cn2 (t )-i

+ D

где D – постоянная.

Это уравнение является уравнением траектории луча для произвольного планарного градиентного волновода. Далее получим это уравнение для градиентного секансного волновода.

Получим уравнение для такого луча, продифференцировав (8) по x :

2. Уравнение траектории луча в градиентном секансном волноводе

В работах [11-12] приведён вывод уравнения луча в градиентном секансном волноводе. Кратко повторим его с помощью уравнения (4).

Пусть распределение показателя преломления задано в виде гиперболического секанса:

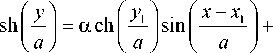
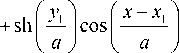
По аналогии с матричными методами расчёта оптических систем будем описывать луч двумя координатами, задающими точку пересечения луча с некоторой опорной плоскостью, а также наклон луча

к оптической оси. Первой координатой будем считать величину sh( y / a ), а второй – ch( y / a ) (d y /d x ).

Тогда из (9) нетрудно получить, что в матричной форме распространение луча описывается следующим уравнением:

a

max

ⁿ 0 ²

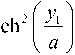
- 1 .

где

sh ^f y I

V a )

f y ) dу (x) chi - I—V a ) dx

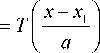
sh ^{f У} 1

V a )

ch f У, ) M x)

V a ) dx

, (10)

T (ф) =

cos ф - sin ф

sin ф cos ф

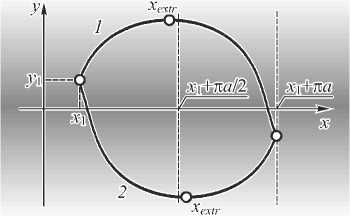
Рис. 3. Планарный гиперболический секансный волновод и световые лучи, соединяющие точку предмета (x₁, y₁) и точку изображения (x 1 + п и, -у 1 )

Из этого уравнения следует, что при x = x 1 + п ma ( m – целое) y = (–1) ^my 1 , независимо от угла наклона луча а . Это означает, что даже для неосевого точечного источника света сохраняется гомоцентричность пучка лучей и формируется точечное изображение.

3. Числовая апертура при построении изображения в градиентном гиперболическом секансном волноводе

Это означает, что при удалении точечного источника от оптической оси числовая апертура лучей, формирующих изображение такого источника, будет уменьшаться. В точке изображения синус максимального угла луча с оптической осью равен:

Очевидно, реальный волновод ограничен по ширине, которая для волновода (5) определяется, например, спадом показателя преломления до единицы. В этом случае не каждый луч, проходящий через некоторую точку, останется в волноводе, часть лучей выйдет через край волновода. Чтобы определить самый крайний луч, найдём точки траектории луча, в которых он максимально удаляется от оптической оси. Для этого в левой части (10) приравняем производную y′(x) к нулю. Тогда получим, что луч максимально удаляется от оптической оси в точках (точки поворота луча) с координатами xextr, удовлетворяющих уравнению th I У1| tg I 'x"----1| = a.                            (12)

V a) V a )

Далее будем рассматривать градиентную линзу, которая представляет собой усечённый волновод длиной п a . Из уравнения (12) видно, что если у 1 и a одного знака, то x extr < x 1 + п a /2 (луч 1 на рис. 3), а если у 1 и а разных знаков, то x 1 + п a / 2 <  x extr <  x 1 + п a (луч 2 на рис. 3).

Согласно (9), (12), максимальное удаление луча от оси описывается следующим уравнением:

sh l y xL | = ± sh² | ^{y 1} | + a ²ch² | ^y 1 I .          (13)

V a ) у V a) V a)

^a max |

sin 9 = '      1V1 + a2L

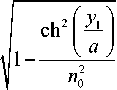
а числовая апертура равна

NA = n (у) sin 9 =

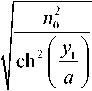
- 1.

Для осевого источника света ( y 1 = 0) числовая 2       ¹²

апертура равна NA = I n 0 - 1 ) , что совпадает с [11].

Для источника на краю волновода (т.е. ch ( y 1 ) = n 0 ) числовая апертура равна нулю и формируемое световое пятно изображения бесконечно расплывается.

4. Построение увеличенного изображения с помощью двух ЛМ

На краю волновода    n ( y extr ) = 1,

значит,

sh ( У extr I^a ) = ( n 2 - 1 )^/ . Из этого условия можно найти максимальный угол наклона a _max, при котором луч не выйдет из волновода, а будет распространяться в нём, формируя в точке ( x 1 + п a , - у 1 ) изображение точечного источника, расположенного в точке ( x 1 , y 1 ):

Рассмотрим градиентную линзу, которая представляет собой усечённый гиперболический секанс-ный волновод длиной п a /2. Такая линза известна как ЛМ [9]. Пусть дана оптическая система, состоящая из двух таких линз с параметрами a 1 = 2L 1 / п и a 2 = 2 L ₂/ п ( a 1 < a ₂, L 1 , L ₂ - длины линз), расположенных вплотную друг к другу (рис. 4). Пусть в передней плоскости первой линзы ( x = x 1 ) расположен точечный источник вблизи оптической оси на расстоянии y 1 ( y 1 <<  a 1 ).

Согласно (11), для обеих линз матрица T имеет вид:

T (ф) =

- 1 0

Тогда из (10) следует, что в задней плоскости первой линзы световые лучи будут описываться координатами:

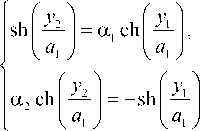
снова соберутся в одной точке и сформируют симметричное относительно оптической оси изображение источника независимо от того, осевой он или

где a ₁ и a ₂ - тангенсы углов наклона луча к оптической оси в плоскостях x ₂ = x 1 и x ₂ = x 1 + п a 1 /2 соответственно.

нет. Однако при a ₁ * a ₂ и у ₁ * 0 изображение сформировано не будет, так как координата y 4 зависит от того, какой угол имел луч с оптической осью в начальной плоскости x = x 1 .

Отношение квадратов гиперболических косинусов в (21) не может превышать единицу, так как a 1 <  a 2 . Источник света расположен недалеко от оси, т.е. y 1 <<  a 1 . Из этого следует, что гиперболические синусы в обеих частях (21) примерно равны своим аргументам и точка пересечения луча задней плоскости второй линзы может быть приближённо определена следующим образом:

_t £1 _{т т} b _r

Рис. 4. Оптическая система из двух ЛМ

Из второго уравнения (18) и близости источника к оптической оси ( y 1 <<  a 1 ) следует (так как ch ( у 2 / a 1 ) >  1), что | a ₂| << 1. Поэтому при записи закона преломления на границе первой и второй линзы можно вместо синусов писать тангенсы:

У 4 =

ch2 f y21 a 2     Ia 2 J a1 Ch2 f У2) ( a1 J

^y 1 ^.

Для луча, выходящего из источника параллельно оптической оси ( a ₁=0), из (18) следует, что у ₂ = 0 и согласно (22)

n ₀

ch

f X1 I al J

a2 =

n ₀

ch

y ₃

a ₂

« з ,

У 4 =

^^^^^^в

a

² y ₁ .

a ₁

где у 3 и a ₃ - расстояние до оптической оси от луча и тангенс наклона луча к оптической оси в плоскости границы двух линз. Очевидно, y 3 = y 2 , т.е. обозначение y 3 введено для единообразия индексов. Снова применим преобразование лучей (10), но уже для второй линзы. Обозначим у 4 и a ₄ - расстояние до оптической оси от луча и тангенс наклона луча к оптической оси в задней плоскости второй линзы (т.е.

Для луча, проходящего через самый край первой линзы, справедливо соотношение: ch( y 2 / a 1 )= n 0 , а значит,

ch

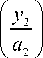
= 2 ( n 0 + ^ n 02 ^{- 1} ) a ² + ( n 0 ^- ^ n 02 ^{- 1} ) a ²

a ₁

a ₁

В частности, при a 2 =2 a 1 получим:

Chly3 ( a 2,

n 0 ^{+ 1}

2,

в плоскости x ₂ = x ₁ + п a 1 / 2 + п a 2 /2):

sh I y ⁴ ) = а з ch I y ³ 1 ,

I a 2 J         I a 2 J

a. ch f У4-1 = - sh f Zl1

I a 2 J       ( a 2 J

Выразив из (19) явно a ₃ через a ₂, выразив явно a ₂ из (18) и подставив полученное выражение для а ₃ в первое уравнение (20), получим:

, X ch2 (1 X sh I ~ 1 =--N sh I У11             (21)

I a 2 J     c_h 2 i y , 1 I a 1 J

I a1 J

Данное уравнение позволяет определить положение точки пересечения луча в задней плоскости второй линзы, зная положение источника в передней плоскости первой линзы. Легко видеть, что если источник света осевой (y1 =0), то все лучи из него соберутся в одной точке и сформируют осевое изображение (y4= 0). Также видно, что при a1 = a2 лучи т.е.

у 4 =^- n ^r ¹ У 1 . ^{(26) n} 0 ²

Это означает, что при a 2 =2 a 1 изображение точечного источника, находящегося на расстоянии y 1 от оси двойной ЛМ из кремния ( n 0 = 3,47), не будет находиться на расстоянии 2 y 1 от оси, а будет расплываться, причём основная доля энергии будет сосредоточена между расстояниями 0,37 y 1 и 2 y 1 от оптической оси.

Численное моделирование проводилось FDTD-методом. Как принято в оптике, оптическая ось обозначим z, а поперечную координату – x. Параметры моделирования были следующими (рис. 4): материал обеих линз – кремний (показатель преломления на оси n 0 = 3,47), длина волны света – 1,55 мкм, длина первой линзы – 1 мкм (ширина – 2,44 мкм), второй – 2 мкм (ширина - 4,88 мкм), расчётная область - 3 Х< x < 3 Х , -0,2 Х< z < 2,5 Х , время моделирования 60 Х / c , где c - скорость света в вакууме, шаг дискретизации по обеим координатам - Х /50, по времени - Х /(100 c ).

Источник света – плоская волна шириной λ/50, расстояние от источника до передней плоскости первой линзы – λ/50. Расстояние от центра источника света до оптической оси варьировалось и составляло 0,1λ, 0,2λ, 0,3λ, 0,4λ, 0,5λ, 0,6λ. Измеритель- ный экран помещался на расстоянии λ/50 от задней плоскости второй линзы. На рис. 5 показаны распределения интенсивности света в плоскости измерительного экрана для всех шести положений источника.

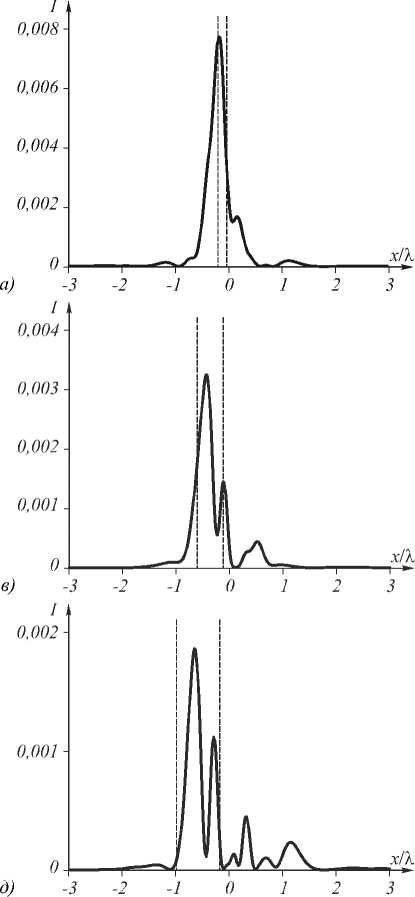
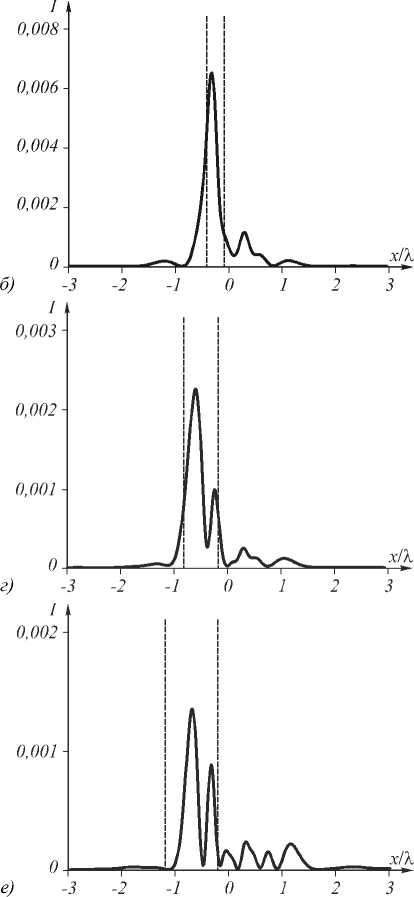
Рис. 5. Распределения интенсивности света в плоскости измерительного экрана для шести положений источника, задаваемых расстоянием от оптической оси: 0,1 λ (а), 0,2 λ (б), 0,3 λ (в), 0,4 λ (г), 0,5 λ (д), 0,6 λ (е)

Вертикальными линиями показаны границы пятна, предсказанные уравнениями (23) и (26). Из рис. 5 видно, что основная энергия сосредоточена как раз в этих границах, за исключением рис. 5 а . На рис. 5 а границы находятся на расстоянии всего 0,163 λ друг от друга, что близко к двумерному дифракционному пределу в кремнии (0,127 λ ). В этом случае геометрооптический подход неприменим и световое пятно не помещается в указанных переделах. Кроме того, при удалении источника от оси возникает два пика интенсивности вместо одного. Это можно объяснить наличием аберраций типа комы.

• 5.    Численное моделирование построения увеличенного изображения со сверхразрешением

с помощью двух ЛМ

В предыдущем разделе показано, что при использовании двух ЛМ разных размеров формируемое изображение имеет линейное увеличение, меньшее, чем отношение размеров линз.

В данном разделе приводятся результаты моделирования построения увеличенного изображения со сверхразрешением с помощью двух градиентных мик-роЛМ, одна из которых в 2,5 раза больше другой. Схема моделирования представлена на рис. 6.

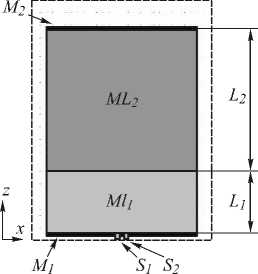
Рис. 6. Оптическая схема изображающей системы с увеличением, состоящей из двух микроЛМ

Свет от двух точечных источников S 1 и S 2 (рис. 6) попадал в линзу Микаэляна ML 1 (источниками могли бы являться, например, два отверстия диаметром 100нм, разделённые расстоянием 100нм, как в работе [13]). В передней плоскости линзы интенсивность света регистрировалась экраном M 1 . Затем свет распространялся через линзу ML 1 длиной L 1 и попадал в линзу Микаэляна ML 2 , длина которой L 2 примерно в 2,5 раза больше L 1 . В задней плоскости линзы ML 2 располагался измерительный экран M 2 . Пунктирной линией показаны границы области моделирования.

Показатели преломления обеих линз распределены по закону гиперболического секанса, т.е. распре- деление показателя преломления всего элемента имеет вид:

n ( x , z )

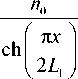
,0 <  z <  L i ,

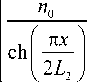
, L 1 <  z <  L 2 .

Параметры моделирования для TE-поляризации были следующими: длина волны света в вакууме X = 1 мкм, материал линзы - кремний, показатель преломления на оптической оси n 0 = 3,47, ширина обеих линз W =4,8 мкм, расчётная длина первой линзы L 1 =2 мкм, расчётная длина второй линзы L 2 = 4,45 мкм. Шаг дискретизации по обеим координатам X /50 = 20 нм, расстояние между источниками - 0,28 X , ширина источников - 0,14 X . Расстояние между источниками и началом первой линзы - 0,1 X , интенсивность поля (| E y |²) на входе линзы (т.е. в плоскости экрана M 1 на рис. 6) показана на рис. 7.

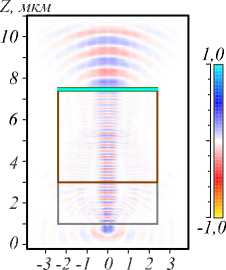
На рис. 8 представлено мгновенное распределение амплитуды E y в момент времени 30,6 X / е , где е -скорость света в вакууме.

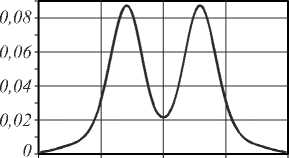
На рис. 8 в плоскости изображения (т.е. в задней плоскости второй линзы) формируется два световых пятна. Усреднённая по времени интенсивность |Ey|2 в этой плоскости, показанная на рис. 9, это под- тверждает, что источники разрешаются по уровню 1/4 от максимума.

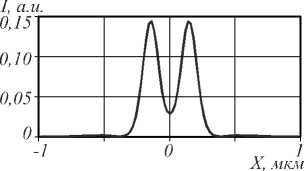
Рис. 7. Интенсивность светового поля в передней плоскости первой линзы

X, мкм

Рис. 8. Мгновенное распределение амплитуды E_y в момент времени 30,6 Х /е

I, а, и.

-1               0               1

X. мкм

Рис. 9. Интенсивность светового поля в задней плоскости второй линзы

Из рис. 9 видно, что расстояние между изображениями источников примерно 0,59 X , т.е. линейное увеличение составляет приблизительно 2,1. Эти два изображения уже можно различить обычной высокоапертурной оптикой с числовой апертурой 0,86.

• 6.    Построение увеличенного изображения со сверхразрешением с помощью расширяющейся ЛМ

На стыке двух линз в предыдущем разделе возникают френелевские потери. Чтобы этого избежать, исследуем линзу Микаэляна, линейно расширяющуюся вдоль оптической оси, т.е. в показатель преломления добавим зависимость от координаты z :

n =

n

ch

^, n x

1 2 L ( z ) J

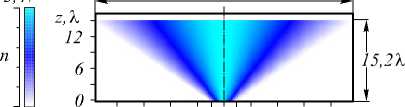
где L ( z ) =2 + 0,5755 z . Распределение показателя преломления такой линзы показано на рис. 10 (в полутонах).

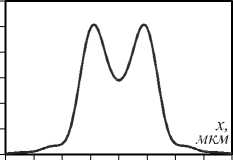
Длина линзы на рис. 10 равна 15,2 мкм, ширина в передней плоскости – 4,8 мкм, в задней – 48 мкм. На рис. 11 приведено распределение интенсивности в задней плоскости линзы при изображении тех же двух источников шириной 0,14 λ с расстоянием между их центрами 0,28λ.

4.8Х

Рис. 10. Распределение показателя преломления (в полутонах) в линзе Микаэляна, линейно расширяющейся вдоль оптической оси 0,06 0,04 0,02 0,00

• -2  -10  12

Рис. 11. Распределение интенсивности в задней плоскости линзы (28) при изображении двух источников шириной 0,14 λ с расстоянием между их центрами 0,28 λ

Расстояние между центрами изображений равно 0,88 λ , т.е. увеличение такой линзы составляет примерно 3,14. Эти два изображения уже можно разрешить обычным микрообъективом с числовой апертурой 0,58.

В разделе 3 было показано, что при удалении от оптической оси даже в случае неувеличивающей линзы, когда пучок лучей сохраняет гомоцентрич-ность и сходится в плоскости изображения, формируемое изображение точечного источника имеет всё больший размер вследствие дифракционного размытия. Это следует из того, что дифракционный предел обратно пропорционален числовой апертуре, которая для системы из двух одинаковых ЛМ имеет вид (16). Если состыковать две линзы разного размера, то лучи из внеосевого источника уже не пересекаются в плоскости изображения, т.е. пятно на изображении будет расширяться не только из-за дифракции, но и из-за нарушения гомоцентричности пучка лучей. На рис. 12 показана зависимость ширины (по полуспаду интенсивности FWHM) светового пятна, формируемого внеосевым источником света с помощью линейно расширяющейся линзы (28). Расчёт проводился FDTD-методом. Параметры расчёта те же самые, что и для рис. 10.

Положение источника менялось от 0 до 2,4 мкм, т.е. вдоль всей передней плоскости линзы (рис. 10). Из рис. 12 видно, что ширина светового пятна на изображении в задней плоскости линзы варьировалась от 0,51 λ до 0,58 λ , т.е. оставалась примерно постоянной, что выгодно отличает линзу (28) от системы из двух линз (27).

На рис. 13 показана расчётная зависимость положения центра светового пятна от положения цен- тра источника света при формировании изображения с помощью линзы (28).

FWHM, X

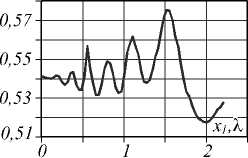
Рис. 12. Зависимость ширины FWHM формируемого изображения от положения точечного источника

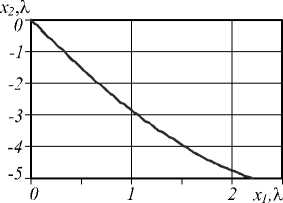
Рис. 13. Зависимость центра фокусного пятна от положения центра источника света

Из рис. 13 видно, что зависимость близка к линейной. Это позволяет ожидать, что при наличии нескольких источников на изображении будут сохраняться пропорции.

Заключение

В рамках геометрической оптики с использованием принципа Ферма получена оценка для положения изображения внеосевого источника, формируемого двумя планарными ЛМ, расположенными вплотную друг за другом. Для системы двух ЛМ, одна из которых в 2,5 раза больше другой, численно с помощью конечноразностного FDTD-метода получено изображение двух точечных источников TE-поляризованного света с линейным увеличением, равным 2,1. Для линейно расширяющейся ЛМ получено линейное увеличение 3,14. В обоих случаях уверенно разрешались два точечных источника, разделённые расстоянием 0,28 λ .

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (соглашение №8027), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и молодого кандидата наук (МК-3912.2012.2) и грантов РФФИ (12-07-00269, 12-07-31117).