Построение в конечных полях вейвлетных фильтров третьего порядка с использованием двучленов специального вида
Автор: Червяков Николай Иванович, Ляхов Павел Алексеевич, Семенова Наталия Федоровна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 2 т.13, 2015 года.
Бесплатный доступ
В работе исследован метод построения вейвлетных фильтров третьего порядка над конечными полями с использованием двучленов специального вида. Использование предложенного подхода позволяет значительно сократить время построения вейвлетных фильтров конечного поля по сравнению с известными методами, основанными на применении алгоритма Берлекэмпа или его модификаций.
Цифровая обработка сигналов, вейвлет-преобразование, алгоритм, конечное поле
Короткий адрес: https://sciup.org/140191750
IDR: 140191750 | DOI: 10.18469/ikt.2015.13.2.01
Текст научной статьи Построение в конечных полях вейвлетных фильтров третьего порядка с использованием двучленов специального вида
Разработка моделей, методов и алгоритмов цифровой обработки сигналов (ЦОС) в конечных полях вызывает в последнее время повышенный интерес у исследователей. Данный факт объясняется особенностями строения конечного поля как алгебраической структуры. В конечных полях, так же как и в полях действительных и комплексных чисел, сохраняется возможность выполнения арифметических операций сложения, вычитания, умножения и деления. С другой стороны, дискретная природа конечных полей эффективна при обработке квантованных величин, возникающих в ЦОС [1].
В настоящее время получило широкое распространение применение вейвлетов для решения разнообразных задач ЦОС. Вейвлет-преобразование возникло как альтернатива преобразованию Фурье – обработка с использованием вейвлетов позволяет получать не только частотную информацию о сигнале, но еще и его локальные особенности. В настоящее время вейвлеты широко применяются для задач сжатия сигнала [2], очистки от шума [3-4], анализа временных рядов [5], обработки данных в медицине [6] и во многих других областях.
Однако в большинстве случаев на практике используются вейвлеты, построенные над полями действительных и комплексных чисел. Особенностью этих вейвлетов является относительная простота построения и применения на практике. Однако вейвлет-преобразование над полями действительных и комплексных чисел не лишено недостатков, к которым прежде всего следует отнести высокую вычислительную сложность обработки, а также неизбежное возникновение ошибок округления.
Для устранения этих недостатков был разработан математический аппарат ЦОС с использованием вейвлетов конечного поля [7]. Предложены методы и алгоритмы кодирования [8-9], криптографической защиты информации [10-11] и обработки изображений [12] с использованием вейвлетов конечного поля. Одним из главных препятствий на пути использования вейвлетов конечного поля на практике является высокая сложность их построения, так как в настоящее время для этой цели используется алгоритм Бер-лекэмпа или его модификации [7]. В данной статье исследованы вейвлетные фильтры третьего порядка над конечными полями, построенные с использованием линейных двучленов специального вида. Представлены алгоритмы построения таких фильтров и приведены примеры.
Вейвлет-преобразование в конечных полях
Конечные поля (поля Галуа) делятся на два типа: простые поля GF^ и полиномиальные поля . Простое конечное поле GF^ содержит число элементов, равное простому числу . Любое конечное поле из элементов изоморфно полю классов вычетов по модулю , поэтому операции сложения, умножения и вычитания в могут рассматриваться как аналогичные операции над целыми числами, взятые по . Арифметика полиномиальных полей является более сложной и осно- вана на свойствах многочленов над GF^p). В данной работе будут рассмотрены лишь простые поля gf(p) .
Пусть мы имеем конечное поле gf(p) . Определим векторное пространство V , элементы которого – вектора над полем GF^p) . Предположим, что это пространство можно представить в виде прямой суммы двух подпространств v = v0®w0,v^w0 = {0}. (1)
Если обозначить через spanyx^a-,,...,«„ линейную оболочку над векторами {»,,«,,...,«„}, то материнский вейвлет ^M и скейлинг-функция р(Д определяющие вейвлет-преобразование в конечном поле GF(pY должны удовлетворять следующим соотношениям [7]
Fo = 8рап)ф(п - 2/)}; V/eZ; (2)
^o = span^n - 2/')}; \/j&Z, (3)
и, кроме того, условиям ортонормированности базиса
YpY1 ~ ^m\ф)п — 2^ = 5^m ~ k)’ Фт, к g Z; (4)
(ip(n - 2m), ip(n -2к^ = 6^m -к), Ут, к eZ; (5)
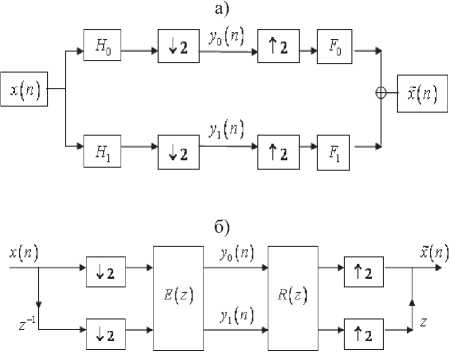
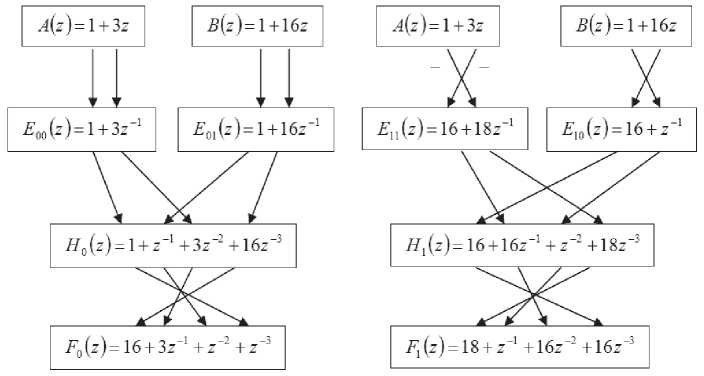
( - 2^)) = 0, \/m,k & Z . (6) Вейвлет-преобразованием в конечном поле GF^p) является отображение, ставящее в соответствие вектору x(m) последовательность коэффициентов (x(m),ip)m -2k)^. Обратное преобразование осуществляется по формуле keZ + ^{^x(m), ip(m - 2k))ip(ii - 2k). На практике вейвлет-преобразование реализуется при помощи наборов фильтров. На рис. 1а показан двухканальный набор фильтров дискретного вейвлет-преобразования. Здесь Hfl и н^ – анализирующие фильтры; 4- 2 – оператор децимации; t 2 – оператор разрежающей выборки; Fo и ^ – синтезирующие фильтры. Этот же набор фильтров может быть представлен в многофазной форме (см. рис. 1б) [13]. С таким набором фильтров ассоциирована матрица E01 (“)4 £u(z)J элементы которой принадлежат кольцу многочленов F(z). В конечных полях, так же как и в полях действительных и комплексных чисел, порядок фильтров, соответствующих материнскому вейвлету ^(.x) и скейлинг-функции ^(^) , должен быть нечетным [7]. Для того, чтобы набор фильтров обладал свойством точного восстановления сигнала, необходимо, чтобы матрица F(z) была параунитарной, то есть выполнялось соотношение Et^z"v')e^) = I , где I – единичная матрица [14]. Необходимым и достаточным условием точного восстановления сигнала является выполнение соотношения Em №oo t’1)+ Em №011’1) = 1 (10) между элементами матрицы (8). Пусть порядок фильтра определяется целым числом 2N + \ иM – положительное число, такое, что M Рис. 1. Двухканальный набор фильтров дискретного вейвлет-преобразования: а) обычное изображение, б) изображение в многофазной форме. EM^^iLevi2" , eiN^0, e„ e GF^p), (12) /=0 а многочлены £io(z) И £11(Z) матрицы (8) находятся по формулам £ю(z) = z"NE»x (z“‘), Д1 (z) = -z"New(z"' ) . (13) Фильтры Яо и H, можно найти по формулам Ho(z)= Eoo(z2)+Z"'SO1(Z"2) Hi(z)= Ew(z2)+ z"*En(z"2)- Фильтры Д И Д находятся из условий точного восстановления сигнала [1] или p = 2"'+3(2Z +1)+1 = 2"'+4Z + 2",+3 +1. Тогда Д Д Y ^i (" Y Д("Y -Яо (- - ) • (16) P Х=Т+г или P 1 =2™+2(2Z + l). Рассмотрим Построение набора фильтров на рис. 1 сводит. М . ся к отысканию многочленовA^z^^a-' ап*0 , и BV^^z' , Ьм + 0 из кольца многочленов f^, удовлетворяющих условию каждый из этих случаев. 1. Пусть r1_2m+^ Если m + 2 четное чи- 1 2 сло, то является квадратичным вычетом по модулю P . Если m + 2 нечетное число, то символ A(z)a(z ’)+ B(z)b(z ’)=1. (17) Лежандра ( /^ m+2 \ = 1, так как p - 8k +1 Каждая такая пара многочленов A(z) и B^ [15]. Следовательно, является квадратич- определяет многочлены Вoo и Ет по формулам ным вычетом по модулю p и при m + 2 нечет- “ = ew; е1( = 0, для i = 0 ... N - М -1; (18) ном. 2. Пусть ^-^2"'+2(2Z + l). Тогда символ Якоби [16] равен Ь,■ =е1(Л,_Л/+,), для z = О ... М. Основной сложностью при построении вейв-летных фильтров конечного поля является поиск многочленов A(z) и 5(з) , удовлетворяющих условию (17). Далее будет исследован вопрос о нахождении многочленов 4(z) и s(z) вида 1 + az в полях GF^ для построения вейвлет-ных фильтров наименьшего нетривиального (третьего) порядка. Построение вейвлетных фильтров третьего порядка в полях GF^ Рассмотрим задачу о построении многочленов A(z)= 1 + az и B^ = \ + bz из GFp\z], для которых выполняется соотношение A(z)a(z~’ )+ B^B^z"' )= 1. Сформулируем и докажем вспомогательное утверждение, которое будет необходимо нам для решения поставленной задачи. Утверждение 1. Число является квадратичным вычетом по модулю p для простых чисел вида p = 8k +1 и p = 8^ + 3 , а для простых чисел вида p = 8k + 5 и p = 8k + 7 является квадратичным невычетом по модулю p. Доказательство. Пусть простое число p имеет вид p -8k + \. Согласно основной теореме арифметики, любое целое число к > 1 представляется в виде учитывая, что — =1 при p = 8k +1. Следова-I P ) тельно, и в этом случае является квадратич ным вычетом по модулю p. Таким образом, p является квадратичным 2 вычетом по модулю P для любых простых чисел вида p = 8k +1. Если простое число p имеет вид p = 8k + 3, то ^1 = 4^ + 1 Символ Якоби для этого случая 2 I 4^ + 1] / , \2A (4A-+11 I , равен (8^ + 3) <4^ + U Если простое число P имеет вид p = 8k + 5, o — 1 то В---= 4Z- + 1. Символ Якоби для этого слу-2 f4£ + 2^ ( 2 Y2A- + C чая равен \8A' + 5y V 8k + 5 Д 8k + 5 J ' «(44+2)7 1 Y J учитывая что 2 яв- 3 7 (2A- + 1J ляется квадратичным невычетом по модулю p = 8k + 5 . k = p1'p<-p; - Если простое число P имеет вид p = 8k + 2, D — 1 то = 4A- + 3 . Символ Якоби для этого случая где F,-,P„ различные простые числа, а a, > 0 ,a, g Z . Равенство (19) можно переписать в виде к = 2"', (777 > 0) или к = 2"' (2Z +1), (77 7 > 0, Z>1). Следовательно, jD = 2",+3+1 равен Обобщая все результаты, описанные выше, заключаем, что является квадратичным вычетом по модулю р для простых чисел вида р = 8/< + 3 и квадратичным невычетом по модулю р для простых чисел вида р = 8к + 5 и р = 8к + 7 . Утверждение доказано. Используя доказанное утверждение, сформу- Окончательно (с учетом порядка следова- ния) имеем пару многочленов и s(z)=l + A(z)=1 + -E^z M 2 удовлетворяющих соотношению A(z)a(z ')+ B(z)b(z )=1 для p = 8k +1 и p = 8k + 3 . Теорема доказана. лируем и докажем следующую теорему. Теорема 1. Для простых чисел вида р = 8к + 5 и р = 8к + 7 не существует пар многочленов 4(z)= 1 + az и B(z)-\ + bz из GF[z], таких, что A(z)a(z"')+ b(z)b(z"') = 1. Для простых чисел вида p = 8k +1 и p = 8/" + 3 многочлены A(z)=l + J? V 2 и 5(z)=l + z (20) Рассмотрим на примере процедуру построения вейвлетных фильтров третьего порядка с использованием теоремы 1. Пример 1. С помощью теоремы 1 найдем многочлены A(z)-1 + az и B(z)= 1 + bz из GF„[z], для которых выполняется соотношение A(z)a(z"' )+ 5(z)5(z-1 )= 1. Полученные многочлены приведены в таблице 1. из GFp\z\ обладают свойством A(z)a(z ')+ B(z)b(z ')=1. Доказательство. Если A(z)= 1 + az и S(z) = 1 + bz, то A^A^z 1) = az + a1 +1 + az1, а s(z)s(z-1) = bz + b1 +1 + bz"1. Следовательно, A(z)a(z 1^+B(z)b(z ') Таблица 1. Многочлены A(z) и S(z) из GF,[z] p = 8k + r j(z) = l + az 5(z)=l + te 3 = 8 ■ 0 + 3 1 + z l + 2z 5 =8-0+5 не существует не существует 7 = 8-0 + 7 не существует не существует 11 = 8-1+3 l + 4z l + 7z 13 = 8-1 + 5 не существует не существует 17 = 8-2+1 l + 5z l + 12z 19 = 8-2 + 3 1 + 3z 1 + 16Z (p + b)z + a + b + 2 + (p + b)z Если A(z)a(z~1)+ B(z)b(z~1)=1 , то a + b = 0 ^b = p - a < или ( . a2 + b2 + 2 = 1 («2+62+l = 0 Из равенства b = p-a следует, что b: = a . С учетом равенства a2 + b2 +1 = 0 имеем, что 2a2 = p-\ или a2 =----. Последнее равенство 72-I возможно в том и только в том случае, если является квадратичным вычетом по модулю p. Используя утверждение 1, заключаем, что если p = 8k + 5 и p = 8k + 7, то многочлены A(z) = 1 + az и B(z)— 1 + bz из <^v[~L для которых A(z)a(z 1)+ B^b(z ' ) = 1 не существуют. Если же p = 8k +1 и p = 8k + 3 , то многочлены A(z) = l + az и B(z) = l + bz из ^14 для которых A(z)a(z ')+ b(z)b(z1 )=1, существуют. В этом случае имеем две пары чисел а и b, удовлетворяющие поставленному требованию: , IP”! a, = J---- и b. = p-A----, а также V 2 V 2 Обратим внимание, что если число p имеет вид p = 2c2 +1, например /2 = 3,19,73,163,883,..., D /2-1 2 МПНГППЛРП то в этом случае ----— c и многочлен A(z) = 1 + az = 1 + cz . В таблице 1 этот случай встречается при /2 = 3 = 2-12+1 и при /2 = 19 = 2-32 +1. Построим теперь вейвлетный фильтр в поле GF(19) с использованием многочленов A(z)=1 + 3z и S(z) = 1 + 16z. Процесс последовательного построения многочленов F!V(z), / = 0,1, y = 0,l из формул (11)-(13), а также анализирующих (Яо и Я,) и синтезирующих ( Fo и F, ) фильтров схематично изображен на рис. 2. Многочлены Л(з) и S(z) из теоремы 1 могут быть использованы для построения других пар многочленов, обладающих свойством A^A^z"1)+ s(z)s(z-1 )= 1. Теорема 2. Пусть Ax(z) = 1 + az , A2(z) = a + z , Mz) = (f - 0+ (f - aV , A4(z) = (p-a)+(p -l)z, B1(z) = l + bz,B2(z) = b + z, B3(z) = (p-l)+ (p-b)z, B4(z) = (p-b)+(p-l)z . Тогда если для многочленов 4(z)и S/(-) из ^„M выполняется соотношение 4(z)4 k'l+^^tz"^!, то для 4(2) иSt(z), где k = 1,2,3,4 и / = 1,2,3,4 выполняется соотношение 4 (z)A, (z"1 )+ Bk (z)Bk (z4 ) = 1. Доказательство. Преобразуем выражения 4(Z)4(A), Л(^)лИ и 4(z)4(z-'): 4 (z)4 (z-1) = az +1 + о2 + az"' = 4 (z)A2 (z~1 ); A (Aa (A ) = (^ - 1X^ - °)- + + (^-1)2 + (^-а)2 + (^-1Х^-«к“' = = az +1 + a2 + az"' = Ax ^Аг (z-1). Аналогично доказывается, что A A)A (A ) = 4 A )4 (A) • Из этих равенств следует, что A/(z)A/(z 1) = az +1 + a" + az для / = 1,2,3,4. Аналогично доказывается, что Bk ^Bk (z-1) = bz +1 + b" + bz"' для k = 1,2,3,4. Так как 4(z)4(z-')+Sl(z)S1(z-1)=l, то и AiW^'V BkWAAVX для 4(z) и BXZV где к = \Д,ЗА и / = 1,2,3,4. Теорема доказана. Рис. 2. Схема построения анализирующих (Но и Н) и синтезирующих (7^ и F) вейвлетных фильтров из многочленов A(z) и В^ в поле GF^ Теорема 2 дает возможность, имея пару многочленов A,(z) = 1 + az и В^)=1 + Ьг, для которых 4 (Z)4 (Z"‘ )+ S1 (Z)B! (--’ ) = L построить с ее помощью еще 15 пар многочленов Л (z) и Bk^Y для которых A^A^-'V BkWkWX • Пример 2. В примере 1 было найдено, что в GF^ для A1(z) = l + 3z и S,(z) = l + 16zвыпол-няется соотношение 4 (z)4 (A )+B! (z)b,(z~' ) = 1 • Используя теорему 2, получим, что A2(z) = 3 + z , A3(z) = 18 + 16z, A4(z) = 16 + 18z , S2(z) = 16 + z , S3(z) = 18 + 3z, 34(z) = 3 + 18z. Комбинируя разными способами 4(z) и Bk(z), где к = 1,2,3,4 и / = 1; 2; 3; 4, получим 16 пар многочленов, удовлетворяющих условию A (z)4 (A)+ Bk Wk (-’’) =1 • Каждая из таких пар может быть использована для построения вейвлетных фильтров третьего порядка над GF(19) аналогично схеме, показанной в примере 1. Заключение В работе исследован метод построения вейв-летных фильтров третьего порядка над полями GF^ с использованием двучленов специального вида. Показано, как предложенный подход может быть использован для построения вейвлет- ных фильтров над полями GF^ при p = 8^ + 1 и p = 8k + 3 . Использование теорем 1 и 2 позволяет значительно сократить время построения вейвлетных фильтров конечного поля по сравнению с известными подходами, основанными на применениии алгоритма Берлекэмпа или его модификаций. Дальнейшая работа в данном направлении может быть направлена на исследование практического применения вейвлетных фильтров третьего порядка для задач ЦОС, а также в кодировании и шифровании. Перспективным подходом к использованию вейвлетов над полями GF(p) является использование модулярной арифметики в системе остаточных классов с простыми модулями. Работа выполнена при финансовой поддержке РФФИ, грант № 14-07-31004-мол-а.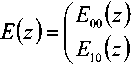
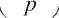
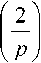
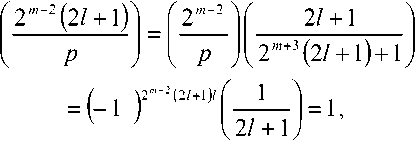
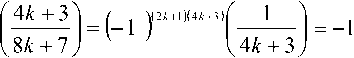
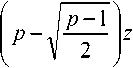
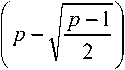
Список литературы Построение в конечных полях вейвлетных фильтров третьего порядка с использованием двучленов специального вида
- Cooklev T., Nishihara A., Sablatash M. Theory of filter banks over finite fields//Proc. IEEE Asia-Pacific Conf. On Circuits and Systems, Taipei, 1994. -Р. 260-265.
- Usevitch B.E. A tutorial on modern lossy wavelet image compression: foundations of JPEG 2000//IEEE Signal Processing Magazine. V.18, No.5, 2001. -Р. 22-35.
- Zhang D., Bao P., Xiaolin Wu. Multiscale LMMSE-based image denoising with optimal wavelet selection//IEEE Transactions on Circuits and Systems for Video Technology. V.15, No.4, 2005. -Р. 469-481.
- Shukla K.K., Tiwari A.K. Efficient Algorithms for Discrete Wavelet Transform With Applications to Denoising and Fuzzy Inference Systems Series. SpringerBriefs in Computer Science, 2013.
- Fu-Chiang Tsui, Li C.-C., Mingui Sun, Sclabassi R.J. A comparative study of two biorthogonal wavelet transforms in time series prediction//Proc. IEEE Int. Conf. on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Orlando. V.2, 1997. -Р. 1791-1796.
- Brechet L., Lucas M.-F., Doncarli C., Farina D. Compression of Biomedical Signals With Mother Wavelet Optimization and Best-Basis Wavelet Packet Selection//IEEE Transactions on Biomedical Engineering. V.54, No.12, 2007. -Р. 2186-2192.
- Fekri F., Mersereau R.M., Shafer R.W. Theory of wavelet transform over finite fields//Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Phoenix. V.3, 1999. -Р. 1213-1216.
- Sartipi M., Delgosha F., Fekri F. Two-Dimensional Half-Rate Codes Using Two-Dimensional Finite-Field Filter Banks//IEEE Transactions on Signal Processing. 2007. V.55, No.12, 2007. -Р. 5846-5853.
- Fekri F., McLaughlin S.W., Mersereau R.M., Schafer R.W. Block error correcting codes using finite-field wavelet transforms//IEEE Transactions on Signal Processing. V.54, No.3, 2006. -Р. 991-1004.
- Delgosha F., Fekri F. Stream cipher using finite-field wavelets//Proc. IEEE Int. Conf. On Acoustics, Speech, and Signal Processing. V.5, 2005. -Р. 689-692.
- Delgosha F., Fekri F. Public-key cryptography using paraunitary matrices//IEEE Transactions on Signal Processing. V.54, No.9, 2006. -Р. 3489-3504.
- Chervyakov N.I., Lyakhov P.A., Babenko M.G. Digital filtering of images in a residue number system using finite-field wavelets//Automatic Control and Computer Sciences. V.48, No.3, 2014. -P. 180-189.
- Vaidyanathan P.P. Multirate Systems and Filter Banks. Englewood Cliffs, NJ: Prentice-Hall, 1993.
- Phoong S., Vaidyanathan P.P. Paraunitary filter banks over finite fields//IEEE Transactions on Signal Processing. V.45, No.6, 1997. -P. 1443-1457.
- Виноградов И.М. Основы теории чисел. СПб.: Лань, 2009. -176 с.
- Сизый С.В. Лекции по теории чисел. М.: Физматлит, 2007. -192 с.


