Построение вейвлет-базисов, адаптированных к дифференциальным операторам

A method of obtaining biorthogonal wavelet bases adapted to linear differential operators is considered. Examples of biorthogonal wavelet bases with compact support are obtained. Using these bases the Galerkin method of solution of differential equations d m u ( x ) /dx^m = f ( x ) supplies diagonal stiffness matrix.

Во многих реальных задачах возникает необходимость решения дифференциальных уравнений, где искомые и/или явно входящие в уравнения функции имеют сингулярности или большие градиенты. При решении уравнений с такими функциями конечно-разностные или спектральные методы становятся либо неустойчивыми, либо не дают необходимой точности из-за возникновения осцилляций вследствие явления Гиббса. Вейвлет-базисы позволяют минимизировать указанные выше эффекты, а также предоставляют возможность построения адаптивных расчетных схем для решения эволюционных уравнений. Тем не менее, применение вейвлет-базисов для решения дифференциальных уравнений все еще не получило достаточного распространения, которое можно было ожидать исходя из их потенциальных возможностей. Одной из причин, на наш взгляд, является сложный, хотя и достаточно разряженный, вид матриц дифференциальных операторов в вейвлет-базисах. В связи с этим возникает потребность построения вейвлет-базисов, дающих наиболее простой вид дифференциальных операторов, входящих в уравнение.

Метод Галеркина

Рассмотрим одномерное линейное дифференциальное уравнение вида

Lu ( x ) = f ( x ),                                 (1)

где u , f g H , H - некоторое гильбертово пространство, например L ²( R ), L -линейный дифференциальный оператор, такой, например, как L = d^m ] dx^m .

Сформулируем основные принципы решения уравнения (1) с помощью метода Галеркина (Петрова – Галеркина). Слабая формулировка уравнения (1) имеет вид

(Lu ( x ), Д) = ( f , p^,                           (2)

где (•, •) обозначает скалярное произведение в соответствующем гильбертовом пространстве, { в _к } — некоторый базис пространства H . Пусть { а _к } - некоторый другой базис пространства H , тогда конечномерная аппроксимация решения u ( x ) примет вид

u ( x ) = Z u j a j .

Подставляя последнее соотношение в (2), имеем

Z uXl«i , в к} = { f , в к ) = f k .                       (3)

Наша задача найти такие базисы a k , в _к , ^пР^и которых матрица жесткости A _jk = L botj , в _к^ имела бы наиболее простой вид. В случае, когда матрица жесткости имеет диагональный вид A jk = A _k 5 j_k , уравнение (3) элементарно разрешимо, u k = A-fk ,    u ⁽ x ) = E A -¹ fa .

k

Если оператор L представляет собой сумму дифференциальных операторов с постоянными коэффициентами L = E N 0 a_k d^kIdx^k , то при использовании базиса Фурье {e ^ik , k е Z } матрица жесткости, очевидно, будет диагональной. Для вейвлет-базисов ситуация сложнее. Тем не менее, имея ортонормированный вейвлет-базис { у _jk ( x ) = 2 j ^/2 у (2 ^j x - k ), j , k е Z } , можно построить биортогональные базисы [1,3,5]

^a jk = L^' k , ^e jk = ^L > jk ,                            ⁽⁴⁾

где L - оператор, сопряженный оператору L . Тогда разлагая решение по базису ajk, а правую часть по базису уjk u=E (u, в j, f=E (f, ^jk} ^jk, j, k                                       j, k подставляя в уравнение (1) и проектируя на базис уjk , получим

E ( u , ^e jk ) ^{L L()}^j k , ^ lm^ = E ( ^f ’ ^ jk } ^ j k     = ^f , У Im ) .

j , k                                       j, k

В силу ортонормированности базиса уjk матрица жесткости будет диагональной: LLajk,ylm^ = (lL’Vjk,ylm^ = (уjk,ylm^ = 5jl5km и решение уравнения принимает простой вид u = E(fУ)ajk • j, k

Так же можно разложить решение u ( x ) по базису у _jk , а правую часть по базису a _jk , тогда решение можно записать в другой форме:

u = E{ f , в Y^j k .

j , k

В случае, когда оператор L самосопряженный и положительно определенный, например L = d ² m/ dx² m , схему решения можно несколько изменить [2]. Представляя оператор L в виде

L = V V , можно определить биортогональные базисы следующим образом: ^a jk = V ^{- 1} y jk , ^e jk = V ^yrjk .

Разложим решение по базису ajk, а правую часть по базису ejk, u=E (u, ejk j, f=E (f, ajk) ejk, j, k                                     j, k подставляем в уравнение (1) и проектируем на базис alm ,

E ( u , ^e jk } k ^L()Cjk ^{, а} 1т^ = E ( ^{f , a} jk ) ( ^e jk ^{, a} im^ = ( f , ^a im ) ^. j , k                                           j , k

Очевидно,     матрица жесткости имеет диагональную     форму:

LLajk ,aim} = V Vajk , V«lm^ = ( VV "ХУ^ , VV "ХУЫ ) = (yjk , У1т ) = 5fl5km и решение уравнения примет вид u= ∑ f,αjk αjk .

j , k

Биортогональные вейвлет-базисы и кратномасштабный анализ

Биортогональные, в частности, ортогональные вейвлет-базисы могут быть получены с помощью так называемого кратномасштабного анализа (КМА) (multiresolution analysis). Биортогональный КМА состоит из двух последовательностей замкнутых аппроксимирующих подпространств пространства L ² ( R ):

⋅⋅⋅⊂ V _{- 2} ⊂ V _{- 1} ⊂ V ₀ ⊂ V ₁ ⊂ V ₂ ⊂⋅⋅⋅ ,

⋅⋅⋅⊂V-2⊂ V-1⊂V0⊂V1⊂ V2⊂⋅⋅⋅, таких, что и?=м u?=м j∈Z                   j∈Z

I ? {", I?>={»}, j∈Z                 j∈Z где черта сверху обозначает замыкание множества. Пространства V , V являются масштабированными версиями центральных пространств V0, V0 соответственно:

f ( ⋅ ) ∈ V ⇔ f (2 ⋅ ) ∈ V 0 , f ( ⋅ ) ∈ V ⇔ f (2 ⋅ ) ∈ V 0 .

Вейвлет-пространство W ( W ) представляет собой дополнение пространства V ( V , соответственно) в пространстве V _{+ 1} ( V _{+ 1} соответственно):

+ 1                        ,         + 1                         .

Условия биортогональности вейвлет-пространств разных масштабов W ⊥ W _′ , ≠ ′ эквивалентны условиям

W 1 r₀, W 1 ^                      (5)

Наконец, существуют функции φ , φ – масштабирующие функции (scaling functions), чьи целочисленные сдвиги образуют базисы Риса (т.е. безусловные базисы) пространств V ₀ и V ₀ соответственно.

V_o = span { ф ( - - k ), k g Z } , ? ₀ = span { ф ( - - k ), k g z } .

Из вложенности пространств V ₀ ⊂ V ₁, V ₀ ⊂ V ₁, следуют так называемые масштабирующие соотношения (scaling relations)

ф( x) = V2 Z Икф(2 x - k), Ф (x) = V2 ^ hi-ij% (2 x — k), kk где hk=φ,φ1k,hk=φ,φ1k, или в пространстве Фурье

ф(5) = mo(^2)Ф(^/2), Ф(^) = mo(^2)ф(^2), где mo (5) = At Z hke~k , kmo(^> = Ат У, hike~k .

2 k                      2 k

Функции m _o( ^ ) и 7 m _o( ^ ) называются низкочастотными фильтрами или масками и полностью определяют КМА. Для выполнения условия биортогональности (5)

достаточно, чтобы масштабирующие функции были биортогональными относительно целочисленного сдвига: ф(-), ф(• - к)^ = 30к , что в терминах масок имеет вид mo (5) 1m 0 (5) + m 0(5 + п) 1m 0 (5 + п) = 1, где черта сверху обозначает комплексное сопряжение. Тогда, определив вейвлет-функции следующим образом:

/5 ) = m ( 5 2) Ф ( 5/ 2) = e "  ⁵ 2 m o ( 5 2 + п ф ( 5 / 2),            (6)

/ ( 5 ) = m 1 ( 5 2) ф ( 5 2) = e "  ⁵ 2 m o ( 5 2 + п ф ( 5 / 2),             (7)

получим биортогональные вейвлет-базисы всего пространства L ²( R ). А именно, обозначив через W ₀ , ( W ₀ ) замыкания множеств целочисленных сдвигов вейвлет-функций:

W_o = span { / ( • - к ), к е Z } , W _o = span { / ( • - к ), к е Z } , получаем, что пространство L ² ( R ) разлагается на прямую (в общем случае неортогональную) сумму вейвлет-пространств W _j ( W _j соответственно)

L ²( R ) = © W = © W ,. j' e Z ^j j e Z ^j

Таким образом, множества функций

/ j_k ( x ) = 2 ^{j /}2 / (2 ^j x - к ), / % _jk ( x ) = 2 ^{j /2} p (2 ^j x - к ), j , к e Z образуют биортогональные базисы пространства L ² ( R ):

(/ к ^ m^ = ³ jl ³ km .

Обозначим через {дк} и {g% к} коэффициенты, соответствующие высокочастотным фильтрам т1 (5) и й% 1 (5) , mi(5)=4- Е дке~ik5, m% 1(5)=-4 2 ^gке~i"5 , 2k                      2k дк = (/, ф1 к У gк = ^Р', (^к \ тогда из (6) и (7) следуют простые соотношения для коэффициентов {дк } и {^дк } :

д к = ( - 1) "l к + 1 , ^д к = ( - 1) ^k h - к + 1 .

Алгоритмы разложения и восстановления по вейвлет-базисам

Помимо того, что КМА дает методику для получения вейвлет-базисов, КМА обеспечивает простую реализацию алгоритмов разложения функции по вейвлет-базису и ее восстановления из вейвлет-коэффициентов.

Пусть нам известны коэффициенты разложения некоторой функции f по масштабирующим функциям самого мелкого масштаба J : c^J _k =(^ f ,фОУ , как правило, в качестве коэффициентов c _k ^J берутся сами значения функции f из дискретной выборки { f k } : c k = fk . Тогда вейвлет-коэффициенты d^J _k=^ f , a _jk^ могут быть вычислены по следующим формулам:

d i - = 2 д . - k C n ,                           (8)

n ci- = Е h.-2 ri .                             (9)

n если сигнал дан N = 2J значениями, то мы имеем N коэффициентов разложения по вейвлет-базису ajk : c 0, dk, j = 0,..., J -1, k = 0,...,2j -1. Формула восстановления имеет вид

c k = E ( % - 2 n^j + ^g k - 2 n ^{d j} ) . n

Как достаточно

мы видели, для вычисления разложения функции по вейвлет-базису

знать лишь коэффициенты низкочастотных { h_k } , { h _k } и высокочастотных

{ g k } , { ^g k }

фильтров. Алгоритмы разложения-восстановления являются более быстрыми, чем БПФ, и при использовании вейвлетов с компактным носителем требуют всего O(N) операций.

Построение биортогональных вейвлет-базисов, адаптированных к операторам вида dm [ dxm

Рассмотрим простейший дифференциальный оператор вида L = d^m / dx^m . Пусть мы имеем ортонормированный базис у _jk , который может быть использован для получения биортогональных базисов по формулам (4). Но непосредственное численное дифференцирование и интегрирование вейвлет-функций, в особенности вейвлетов с компактным носителем типа Добеши, весьма неустойчивая и трудоемкая операция. Кроме того, для применения быстрых алгоритмов разложения и восстановления (8) – (10) необходимо знать соответствующие масштабирующие функции, т.е. низкочастотные фильтры (маски), которые в общем случае нельзя получить применением операторов L - и L к масштабирующей функции ф , определяющей ортонормированный вейвлет-базис.

Пусть m ₀ низкочастотный фильтр (маска), определяющий ортонормированный вейвлет-базис, образованный функциями у _jk с N нулевыми моментами, тогда

- ф mо(^) = —— Q(f), Q(п) # 0,

V 2 7

где в случае использования функций с компактным носителем Q (ф)-тригонометрический полином.    Используя соотношение,    связывающее масштабирующую функцию с маской m0 ,

^

ф (ф ) = C П m о ( 2"Ч),

j = 1

где константа C определяется нормировкой функции ф, и классическую формулу го

П cos (- -)        , j=1                    к можно показать, что маски, соответствующие вейвлетам ajk = !/ уjk , Pjk = Гуjk, где

L = d m I dx m , выражаются следующим образом: /        _e n m             /        _e n N + m

(i + - - if A           (i + -iф mo“(^) =           m о(Ф) =             Q (f),

V 2 7 V 2 7

m о ^в ( f ) =

Г 2 e - ^{i f}

V 1 + e - ^{i f}

.к_Хц_ге - f V - m m о ( ф ) = e - i^{m f} —e—     Q ( f ).

V 2 7

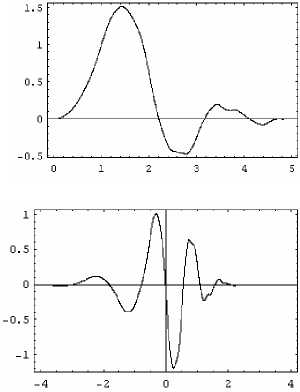
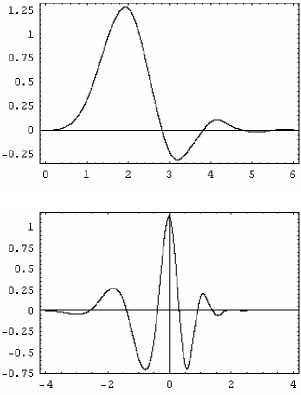
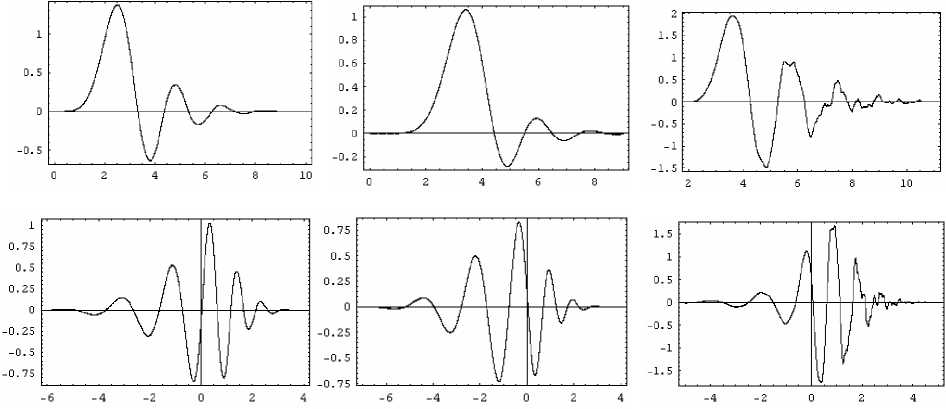
На рис. 1, 2 изображены биортогональные масштабирующие функции и вейвлеты, адаптированные к операторам d ² dx ² и d ⁴ dx ⁴, полученные из ортонормированных вейвлет-базисов Добеши 5-го и 10-го порядка.

а

б

с

Рис. 1. Масштабирующие функции (верхний ряд) и вейвлеты (нижний ряд), адаптированные к оператору d ² dx ² , построенные на основе вейвлета Добеши 5-го порядка. Вейвлет Добеши (а); биортогональные вейвлеты α (б) и β (с)

а

б

с

Рис. 2. Масштабирующие функции (верхний ряд) и вейвлеты (нижний ряд), адаптированные к оператору d ⁴ dx ⁴ , построенные на основе вейвлета Добеши 10-го порядка. Вейвлет Добеши (а); биортогональные вейвлеты α (б) и β (с)

Необходимо отметить, что операция дифференцирования (интегрирования) не коммутирует с операцией масштабирования. А именно, определим оператор масштабирования следующим образом:

Df=21/2f(2⋅), тогда d—Djf (x) = 2jmDj—f (x), m, j eZ. dxm      ( )          dxm ( )

Таким образом, матрица жесткости при использовании алгоритма анализа-синтеза в силу того, что действие алгоритма сводится к масштабированию продифференцированных (проинтегрированных) вейвлетов, имеет диагональные элементы вида 2-jm и решение уравнения запишется в виде u = ^ 2jm f/ ,«jk j .

j , k

Примеры решения уравнений

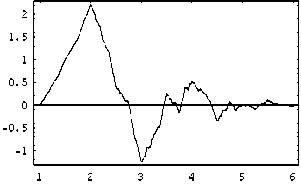
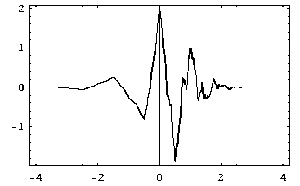
Приведем примеры решения уравнений 2-го и 4-го порядка с разрывными правыми частями. На рис. 3 приведены решения уравнений d ² u/dx ² = f ( x ) и d⁴ u] dx ⁴ = f ( x ), x e [ 0,1 ] с периодическими граничные условиями

u ⁽ n ) (0) = u ⁽ n ) (1), n = 0,1,..., m — 1, условием совместности и условием однозначной разрешимости 11 j f ( x ) dx = 0, J u ( x ) dx = 0. 00

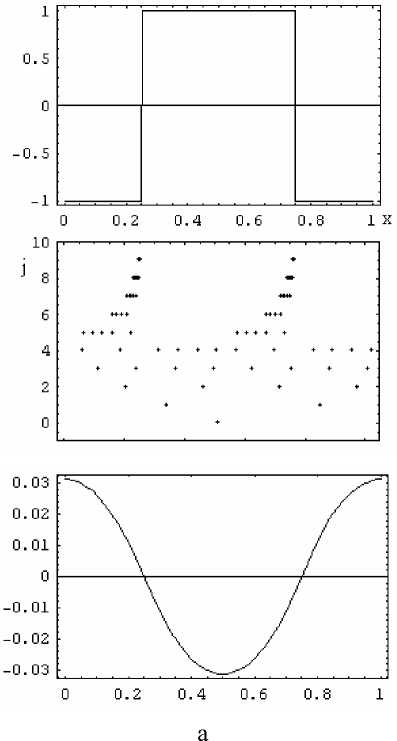
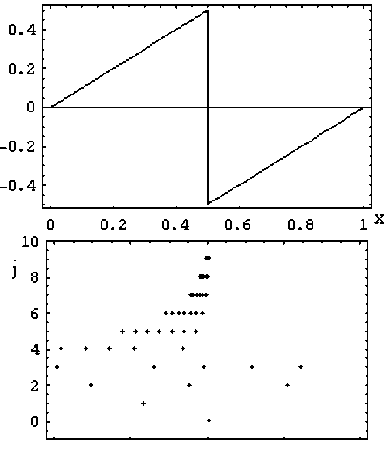
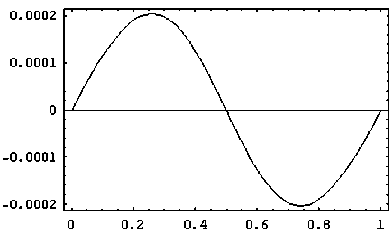
б

Рис. 3. Примеры решения дифференциальных уравнений 2-го порядка (а) и 4-го порядка (б). Верхний ряд: графики правых частей уравнений; средний ряд: сетки существенных вейвлет коэффициентов (больших малого порогового значения, по вертикальной оси отложен индекс масштаба); нижний ряд: решения уравнений

Отметим, что в отличие от спектральных методов, представление разрывных функций с помощью вейвлет-базисов достигается лишь небольшим количеством существенных коэффициентов.

Заключение

Как мы видели, биортогональные вейвлет-базисы в принципе позволяют решать дифференциальные уравнения не менее эффективным способом, чем при использовании базисов Фурье. Более того, представление функций с резкими градиентами (разрывами) требует существенно меньшего числа степеней свободы. К сожалению, построение вейвлетов, адаптированных к более общим дифференциальным операторам, таким как сумма дифференциальных операторов с постоянными коэффициентами, затруднено тем, что теперь биортогональные вейвлеты не являются инвариантными относительно масштабирования. Отдельной проблемой остается удовлетворение граничных условий. Таким образом, назревает потребность обобщения понятия вейвлет-базиса, когда вейвлет-функции не инвариантны относительно сдвига и масштабирования [4].

Первый автор (В.Г. Захаров) выражает благодарность за финансовую поддержку Американскому фонду гражданских исследований и развития, грант № PE-009-0.