Построение векторных моделей с использованием промежуточных аргументов

Метод математического моделирования векторных замкнутых контуров достаточно подробно освещен в работах [1, 2], и успешно применяется для моделирования механизмов, применительно к задачам анализа и синтеза, а в более широком смысле и композиции механизмов (синтеза структурной или кинематической схемы механизмов обеспечивающих требуемую передаточную функцию). Основу метода составляют векторные замкнутые контуры, состоящие из отдельных векторов. Вектор – это направленный отрезок с параметрами r и а i (рис. 1).

Известно, что любую структурную схему механизма можно отобразить векторным контуром (рис. 2).

Подобные векторные замкнутые контуры можно привести к виду элементарных векторных замкнутых контуров – модулей, с заранее известными и подробно описанными решениями, определяемые из условий замкнутости векторных контуров (1) и (2).

Условие замкнутости m -векторного контура на плоскости:

mm

^ ri cos ai = 0; ^ ri sin ai = 0.

i=1

Условие замкнутости m -векторного контура в пространстве:

m

m

^ r i cos a i cos P i = 0 ; ^ r i sin a i = 0

im1i

^ r i cos a i sin ^p i = 0 .

i = 1

Основные сочетания функций возможных векторных контуров исходя из условия замкнутости определяют четыре плоских элементарных Косенок Борис Борисович, кандидат технических наук, доцент кафедры основ конструирования машин.

модуля(Пл1-Пл4)) и двадцать пространственных (Пр1-Пр20) [1]. Это позволяет строить систему векторных контуров, достаточно простым методом подбора требуемых модулей.

Построенная на основе модулей основная векторная модель позволяет получить решение определенных функций, с известными для каждого момента времени аргументами модели и связями между отдельными векторами и контурами.

Простые векторные модели, состоящие даже из множества векторных контуров, позволяют решать, например, задачи теории машин и механизмов в рамках анализа и синтеза механизма, но не позволяют решать все задачи моделирова ния, которые стоят перед проектировщиками.

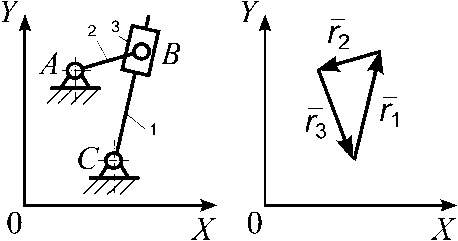
Рис. 2. Структурно схема(а) и векторная модель(б) механизма

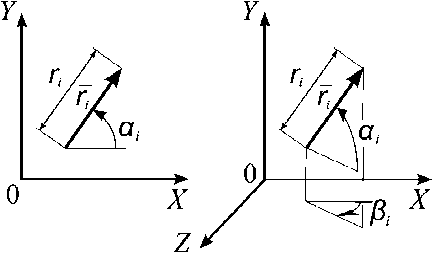
Рис. 1. Параметры плоского и пространственного вектора

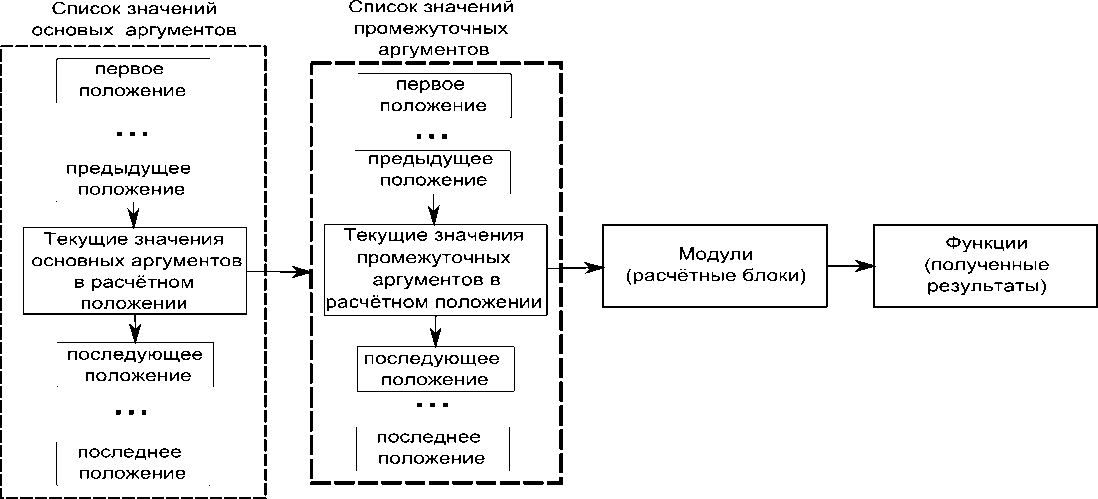
Рис. 3. Схема расположения промежуточных аргументов в системе расчета векторных модулей

Различные задачи исследования и проектирования механических устройств, привели автора к необходимости использовать инвариантность векторных моделей в моделировании более сложных объектов – различных траекторий, площадей, объёмов и т.д., что и было найдено с введением новых расчетных векторных моделей с использованием так, называемых промежуточных аргументов.

В общем случае, промежуточные аргументы -это аргументы или изменения параметров вектора для построения нескольких положений векторной модели в одном положении основных аргументов. Тем самым, как бы проводится изменение векторной модели не только от одного положения к другому (от одного значения основных аргументов к другому), но и изменение векторной модели в одном положении (от одного значения промежуточных аргументов к другому) (рис. 3).

Например, роторно-поршневой двигатель (РПД) Ванкеля можно смоделировать с помощью векторного моделирования, так, как приведено на рис.4.

Простейшая векторная модель моделирует отображенная на рис. 4.в моделирует движение точки А, в то время, как расширенная модель, отображённая на рис. 4.г позволяет строить профиль камеры сгорания роторного двигателя в каждый момент времени.

Принципиальная разница этих моделей, состоит не в сложности второй относительно первой, а в том, что для описания движения составных частей двигателя в векторной модели (рис. 4.в) используются основной аргумент, описывающий изменение поворота ротора двигателя во времени и этого достаточно для проведения кинематического исследования РПД Ванкеля, в то время как, в расширенной векторной модели (рис. 4.г)

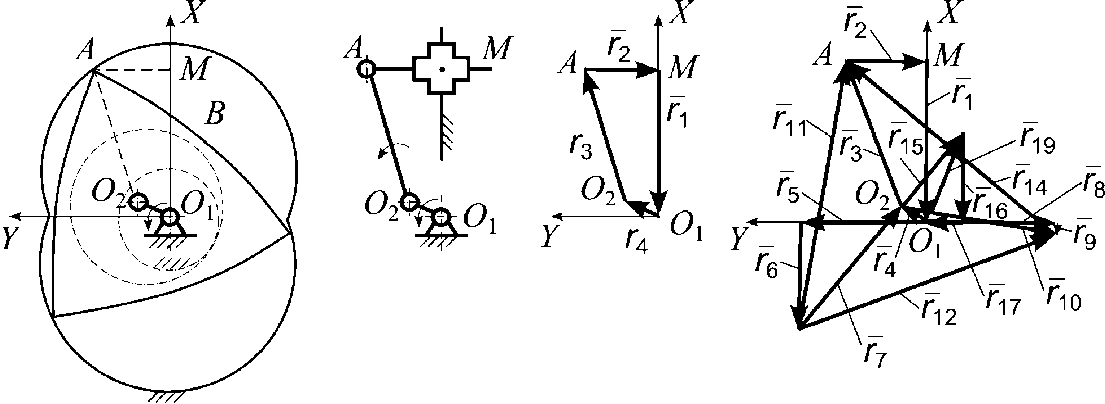
а)                   б)                 в)

г)

Рис. 4. Конструктивно-структурная схема(а) РПД Ванкеля и замещающая рычажная схема(б), его векторная модель (в) и расширенная векторная модель(г)

возможностью непосредственного соединения с

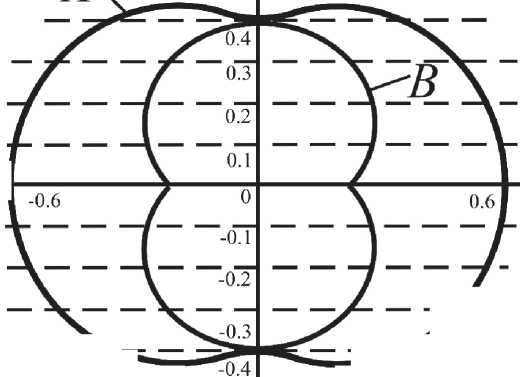
\     0.4352 6^ / _     _ _\o£X _ /          1       02           1 I -o.6      !     о        д       06L T        1      01         1        / "X^     \ "°2      /     / -0.43526 Рис. 5. Траектории движения точек A и B векторной модели РПД используются промежуточные аргументы, позволяющие строить как движение характерных точек А и В(описывающих, как движение ротора в корпусе), так и множества точек принадлежащий внутреннему профилю корпуса двигателя(рис. 5). Построение полной траектории данных точек в каждом расчетном положении, необходимо для решения задачи нахождения объема рабочей камеры двигателя, что требуется для построения индикаторной диаграммы давления в рабочей камере, которое в свою очередь необходима для проведения исследования динамического поведения двигателя. Удобство работы с промежуточными аргументами заключается и в том, что плотность точек описывающих площадь камеры сгорания, можно легко уменьшать или увеличивать, то есть оперативно изменять точность в процессе работы с моделью, что проистекает из параметрической основы векторных моделей. Ещё один пример применения векторных моделей с промежуточными аргументами относится к расчетам шестеренных насосов. Шестеренные насосы (рис. 6) обладают простотой конструкции, малой трудоемкостью изготовления, сравнительно небольшими габаритами и массой, П I Г        AW, Ate 1             . i' )      \ i                               -Х-XXL/’ —U --V^^-------J-------х=^ц=^-------k-^x--- ХжХ- - ^— Рис. 6. Схема шестеренного насоса

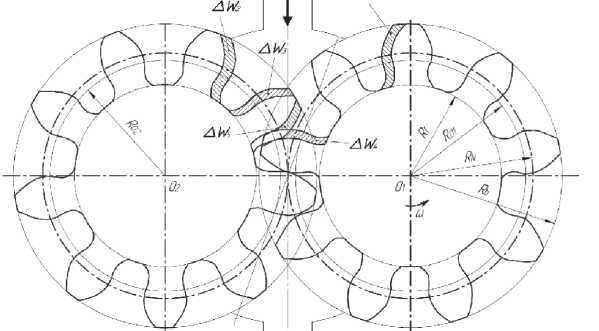
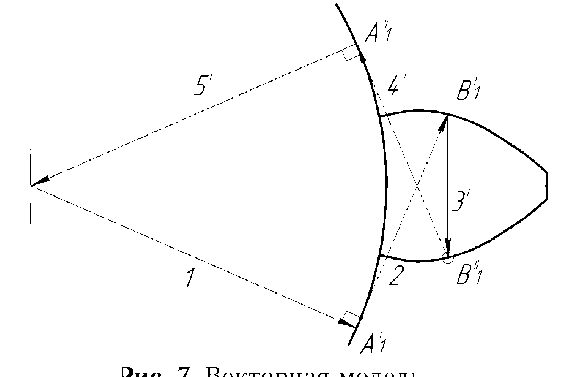
быстроходными двигателями. В тоже время к недостаткам шестеренных качающих узлов следует отнести чувствительность к механическим примесям в перекачивающей жидкости; рост зазоров в процессе эксплуатации, вызывающий увеличение утечек; неравномерность подачи жидкости и высокий уровень акустического шума. Для снижения интенсивности колебательных и кавитационных процессов необходима разработка методов оперативного и адекватного учета кинематической подачи жидкости при измененной геометрии профиля зубьев насоса. В рамках разработки методики анализа и диагностики пульсаций подачи жидкости шестеренным насосом была создана математическая модель зубчатого зацепления сопрягаемых поверхностей на базе векторной модели с промежуточными аргументами (рис. 7). Более подробно разработка и проверка как самого метода, так и векторной модели освещены в статьях [3, 4]. Результаты эксперимента по проверке новой методики анализа и диагностики пульсаций подачи жидкости шестеренным насосом приведены на рис. 8. Сравнение по среднеквадратичному значению амплитуд пульсаций Рис. 7. Векторная модель, описывающая отдельный зуб шестерни 400 p----T------T--------------T------T------т------- Я 200         \           \           \           \ - “   A A A A i "&z ж'жж \ t^-200 F        ‘ f -4001----------1----------1----------1-------—1----------1----------1----------IO3 0      2      4      6      8     10     12     14 Время, c ------ Предлагаемая мидель — — Эксперимент ■ • ■ — Традиционная модель Рис. 8. Результаты эксперимента

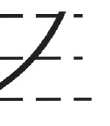
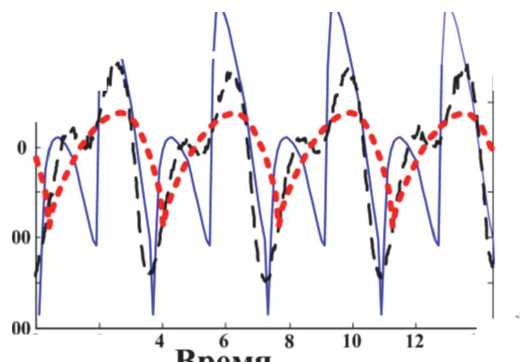
давления предлагаемой и ранее существующей моделей с экспериментом показало, что предлагаемая модель точнее существующей на 25-30% в зависимости от режима работы шестеренного насоса.

Использование векторных моделей с промежуточными аргументами и в этом случае дали возможность простыми методами и трудозатратами наглядно и быстро решить задачу построения и взаимодействия различных деталей насоса.

При выполнении работ в рамках исследований [5, 6] автором статьи была предложена векторная модель воспроизводящая кинематику шариков подшипника качения.

В опорах авиационных газотурбинных двигателей для восприятия осевых и радиальных нагрузок применяются шариковые подшипники. Величины нагрузок существенно зависят от режима работы двигателя. Величина радиальной нагрузки определяется весом ротора и величиной дисбаланса, а величина осевой - разностью газодинамических сил компрессора и турбины. Для обеспечения нормальной работы необходимо знать влияние изменения геометрии подшипника и его составных частей, а также нагрузок на динамику подшипника. Схема усилий в контактах с учетом центробежных сил шариков при двухточечном контакте приведена на рис 9.

Для подобного анализа предложена векторную модель точек контакта колец и шарика подшипника качения (рис. 10), полная векторная модель с использованием промежуточных аргументов представлена на рис. 11.

В эксперименте описанном в работе [6] оценивалось радиальное перемещение внутреннего кольца подшипника относительно наружного при

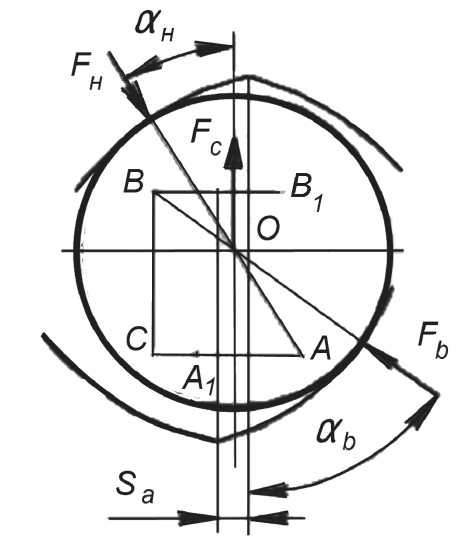
Рис. 9. Схема усилий в контактах шарика с учетом центробежных сил

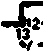
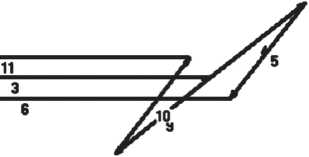
Рис. 10. Векторная модель точек контакта колец и шарика подшипника качения

различных уровнях нагрузки радиальной и осевой силой для нескольких значений оборотов ротора. Радиальная нагрузка на подшипник складывалась из веса ротора и динамической нагрузки от его дисбаланса. Сравнивая результаты полученные экспериментально с расчетными можно говорить о том, что погрешность не превышает 15-20 % (рис. 12).

Приведённые примеры использования векторных моделей с промежуточными аргумента-

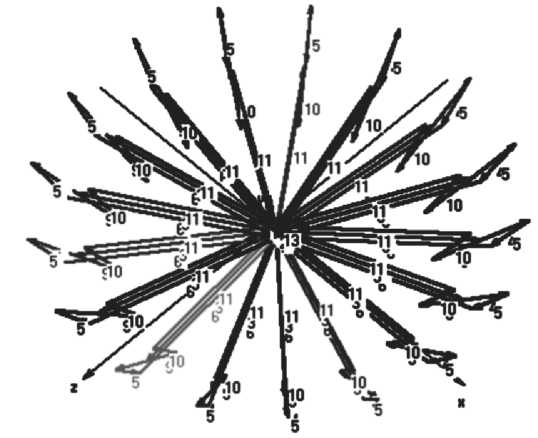
Рис. 11. Полная векторная модель подшипника качения

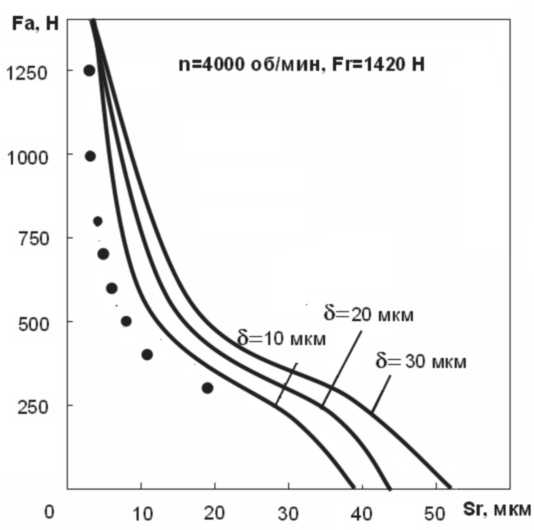
Рис. 12. Осевые усилия на подшипник ми, показывают, что такие параметрические векторные модели с одной стороны, обладают достаточной простотой и позволяют оперативно добиваться нужной точности вычислений (увеличивая или уменьшая шаг промежуточных и основных аргументов модели), а с другой, при описании сложных траекторий, поверхностей, и объёмов, обладают визуальной наглядностью, и являются системой ранее отлаженных расчётных блоков (модулей), что позволяет обеспечивать надежность полученных результатов. Использование промежуточных аргументов позволяет использовать векторные модели как для решения основных задач, так и для расчета вспомогательных задач, в рамках единой расчётной модели.