Построение винтовых поверхностей технических форм

Большое количество машиностроительных форм, в том числе и металлорежущего инструмента (метчики, фрезы, сверла, зенкеры и пр.) имеют в своей основе винтовые поверхности. Эти поверхности применяются для формирования режущих кромок, размещения стружки и смазочно-охлаждающих жидкостей. Кроме того, винтовые поверхности в различных вариантах зубчатых колес, червяков, валов участвуют в передаче механического движения. Качественное изготовление винтовых поверхностей в большой степени зависит от специальной теории, которая рассматривает различные способы образования винтовых поверхностей.

Винтовая поверхность получается в результате винтового перемещения образующей. Точки образующей во время винтового движения описывают винтовые линии, каждая из которых может служить направляющей винтовой

поверхности. Полученные лини называют винтовыми параллелями. В представленной статье показано два варианта получения винтовых параллелей в зависимости от варианта выбора координации пространства. Одним из свойств винтовых поверхностей является возможность «сдвига», т. е. перемещение вдоль оси винтовой поверхности во время винтового перемещения. Благодаря этому винтовые поверхности находят широкое применение в машиностроении: шнеки горнопроходческих, снегоуборочных и сельскохозяйственных машин, винтовые лестницы, сверла, винты, пружины, змеевики и многие другие варианты применения винтовых поверхностей.

Развитие способов формообразования поверхностей в специальных координатах требует применения к такой координации пространства уже известных конструктивных схем и способов. Одними из наиболее распространенных в технике являются винтовые поверхности, которые образуются винтовым движением представленной образующей линии. Такие поверхности можно получить путем изъятия из конгруэнции, цилиндрических винтовых линий, имеющих общую ось и постоянный шаг.

Для формообразования винтовых поверхностей применяют различные криволинейные координаты. И выбор этих координат зависит от конкретных условий формообразования винтовых поверхностей. В случае необходимости создания общего для винтовых поверхностей метода профилирования инструментов, его создание возможно в случае, когда профили винтовых поверхностей будут заданы одними и теми же параметрами криволинейных координат. Так как винтовые поверхности обладают возможностью «сдвига» в направлении винтовой линии, то за первую координату обычно принимают винтовую линию, а второй координатой может быть произвольная линия, находящаяся на винтовой поверхности. В данной статье рассматриваются варианты замены нормальной цилиндрической координации пространства путем ввода новой конгруэнции координатных линий. Делается это путем замены одной из двух семей координатных линий на опорном цилиндре на семью винтовых линий.

Одним из вариантов применения винтовых поверхностей являются цилиндрические косозубые колеса эвольвентного профиля. Зубчатые колеса используют для передачи движения и усилия с одного вала на другой. Передача этого усилия происходит за счет сцепления рабочих поверхностей зубьев. Поэтому к зубчатым передачам применяют различные кинематические и прочностные требования, которые обеспечивают их качественное функционирование. Работа зубчатых колес в значительной мере зависит от геометрических параметров зубьев, находящихся в зацеплении, размеров самих колес и параметров зуборезных станков. В настоящее время наиболее распространенные зубчатые передачи имеют поверхности зубьев эвольверт-ного профиля, которые имеют достоинства по cравнению с другими поверхностями зубьев зубчатых колес. В приведенной статье показана возможность моделирования теоретической боковой поверхности цилиндрического косозубого колеса эвольвентного профиля путем создания внутреннего уравнения на основе цилиндрической системы координат. При этом на поверхности опорного цилиндра семейства линий t, u, v заменяются конгруэнцией винтовых линий. В результате в значительной мере облегчается моделирование сложного эвольвентного профиля зубьев.

Основной целью являлась разработка аналитической модели конгруэнции координатных линий нормальной цилиндрической системы, которая образуется при замене одного из семейств координатной сетки опорного цилиндра на семью винтовых линий постоянного шага. В работе [1] были рассмотрены конгруэнции координатных линий нормальных систем, которые образуются за счет изменения одного из двух семейств линий координатной сетки опорной поверхности.

МЕТОДИКА ИССЛЕДОВАНИЙ

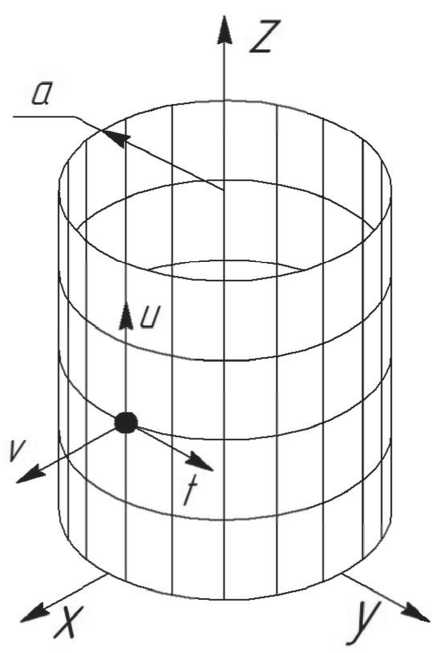
Рис. 1. Опорный цилиндр нормальной цилиндрической системы координат

Система нормальных цилиндрических координат (рис. 1) в классическом виде записывается в виде функций:

x = (a + v )cos t, y = (a + v )sin t, (1)

z = u, где: t – угловая координата, отсчет которой осуществляется в направлении против хода часовой стрелки от плоскости XOZ до полуплоскости расположения текущей точки;

u – расстояние от плоскости z=0 до текущей точки на поверхности цилиндра (координата u может быть положительной либо отрицательной);

v – расстояние от текущей поверхности опорного цилиндра до точки пространства вдоль нормали;

а – радиус опорного цилиндра.

Следует отметить, что координаты р и и образуют прямоугольную декартову систему координат на плоскости с осью Oz при условии t=const, а соответственно координаты p=a+v и t в совокупности будут образовывать полярную систему координат в плоскости xOy (при u=const).

Поверхности v=const являются цилиндрами, которые будут соосны с опорным цилиндром. Если рассмотреть координатные поверхности систем: t=const и u=con st, то они будут представлять собой плоскости, которые перпендикулярны к оси 0z и проходят через ось опорного цилиндра.

При определении конгруэнций линий необходимо выделить следующие:

• -    конгруэнция v - линий, образуется при помощи нормалей опорного цилиндра;

• -    конгруэнция u - линий, образуется совокупностью прямых, которые будут параллельны оси опорного цилиндра;

• -    конгруэнция t – представляет собой множество окружностей, центры которых расположены на оси опорного цилиндра и будут пересекаться плоскостями расположенными перпендикулярно к опорному цилиндру.

Поменяем заданную нормальную цилиндрическую координацию пространства (1) путем ввода новой конгруэнции координатных линий. Сделать эту замену можно следующим способом: поменяем одну из двух семей координатных линий на опорном цилиндре на семью винтовых линий. В результате этой замены будут получены два варианта новой координации.

В первом варианте координатная сетка на опорном цилиндре, вместо окружностей и прямолинейных образующих будет состоять из множества прямолинейных образующих винтовых линий пересекающих их под постоянным углом - р . Для получения данного семейства линий, необходимо заменим параметр u. Сделать это можно при помощи непрерывной дифференцированной функции [2] двух переменных:

U = U (t, W) , (2)

где w – параметр семьи линий винтовых линий, которые располагаются на поверхности определителе.

Если воспользоваться уравнением для нахождения угла между двумя направлениями на поверхности, то получим выражение функции (2)

COS ф = .                       X

• 4 Edu ² + 2 Fdudt + Gdt²

Edu d u + F ( du d u + dt d t ) + Gdt d t   (3)

4 E d u ² + 2 F d u d t + G d t²

где E = 1 , F = 0 , G = a ² - коэффициенты первой квадратичной формы опорного цилиндра.

Направление прямолинейных образующих опорного цилиндра [3] можно определить выражением д u = 1, д t = 0 . Учитывая эти выражения и значения коэффициентов E, F и G уравнение

• (3)    будет выглядеть следующим образом: du

и ² + a² dt ² .

cos в = —j= d

Если в данном уравнении разделить переменные получим следующее выражение:

du = ± a ctg в dt .            (4)

Решая данное уравнение получим:

u = ± a ctg в t + w .          (5)

Знаку ± в данном выражении будут соответствовать: правое направление винтовой линии – знак «+», левое направление винтовой линии – знак «-».

При подстановке правой части выражения (5) в выражение (1) вместо значения u получаем следующие функции:

x = (a + v )cos t, y = (a + v) sin t,               (6)

z = ± a ctg в t + w .

В результате получены уравнения, которые определяют новую нормальную цилиндрическую координацию пространства. В результате этой замены семья u=const , которая представляет собой совокупность прямых, параллельных оси опорного цилиндра, заменена семьей прямых геликоидов ( w=const ). Эта семья образуется нормалями опорного цилиндра вдоль винтовых линий. Конгруэнцию t – линий в новой координации пространства опорным цилиндром образуют пары поверхностей w=const и v=const . Эти пары поверхностей определяют множество винтовых линий, которые в соответствии с выражением (6) будут иметь постоянный шаг b=a ctg p .

Связав параметры w и v с помощью непрерывной дифференцируемой функции, получим внутренние уравнения поверхности новой конгруэнции координатных линий:

v = v ( w ), t = t, или w = w ( v ), t = t .

Если в уравнение (6) подставить правую часть уравнения (7) можно получить параметрические уравнения поверхности конгруэнции. Так как каждому значению параметра t в функциях (6) соответствует полуплоскость пучка с осью Oz , то функции w=w(v) или v=v(w) при этом определяют некоторую плоскую линию, которая лежит в этой полуплоскости.

Во втором варианте на опорном цилиндре координатная сетка будет состоять из семьи окружностей с центрами на оси цилиндра, которые принадлежат плоскостям перпендикулярным к ней, и семьи винтовых линий, которые образуют постоянный угол y = n /2- в с этими плоскостями.

Если записать уравнение (4) относительно dt , при этом учитывая значение угла наклона винтовых линий у получим:

dt = ±

du

a tg Y

Решением этого выражения будет: u

t = ±--+ w.

a tg Y

При подстановке уравнения (8) в функции (1) вместо значения t получаем:

u x = (a + v) cos(±--+ w), a tg Y y = (a + v) sin(± — --+ w),      (9)

a tg Y

z = u

В отличие от первого варианта в данном случае в параметризации опорного цилиндра сохранено семью плоскостей u=const . Конгруэнции w=const будет соответствовать однопараметрическое множество прямых геликоидов соосных с осью опорного цилиндра, а семейство u – линии, образует конгруэнцию винтовых линий.

Функции, которые будут определять внутренние уравнения поверхности конгруэнции винтовых линий, будут записаны в виде:

V = v(w), u = u , или w = w(v), u = u . (10)

При этом стоит обратить внимание, что приданной координации пространства [4] на поверхности опорного цилиндра можно выделить два семейства линий:

• -    винтовые линии, находящиеся на поверхности опорного цилиндра;

• -    плоские линии, находящиеся в плоскостях перпендикулярных оси опорного цилиндра и соответствующие текущему значению параметра u .

Полученные результаты позволяют связывать с выражениями (6) и (9) возможность погружать в конгруэнцию винтовых линий некоторую плоскую линию. Погруженная линия, совершая движение вдоль оси опорного цилиндра, будет находиться:

• -    в плоскости перпендикулярной оси опорного цилиндра, если применяется координация пространства в соответствии с функциями (9);

• -    в плоскости, которая проходит через ось опорного цилиндра, если применяется координация пространства в соответствии с функциями (6).

Исследуем эти свойства, рассмотрев конкретные примеры в области машиностроения.

Пример 1. Составить уравнение поверхности, образованной левым винтовым движением окружности, которая находится в плоскости, проходящей через ось вращения.

Искомую поверхность получим, погружая окружности в конгруэнции (6) винтовых линий [5]. Пусть плоскость окружности определяется значением параметра t=t0 [6, 7]. Параметрические уравнения (6) будут иметь вид x = (a + v) cos t0, y = (a + v )sin t0,              (11)

z = - a ctg pt0 + w и будут определять плоскую систему прямоугольных координат, оси которой v, w параллельны осям системы p = ^x2 + y2 , z с началом в точке O‘, которая имеет координаты r0=a, z=-actgb.

Подставляя в уравнение заданной окружности f         y i x = ^tg t ₀;

l(p - Pc)2 + (z - zc)2 = R2, вместо x, y, z правую часть выражений (11) и учитывая, что r=a+v, преобразуем эти уравнения в

• t = t 0 ;

• <         ( a + v - P c )² +

+ ( - actg p 1 ₀ + w - z c )² = R ².

Решая последнее из уравнений системы относительно w получим:

w = zc ± VR2 - (a + v - Pc)2 +

+ a ctg в 1 ₀

внутреннее уравнение поверхности. На рис. 2 изображена поверхность, построенная по полученному внутреннему уравнению.

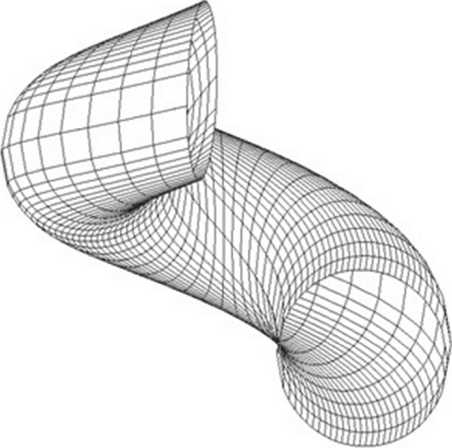
Рис. 2. Поверхность к примеру 1

( 0 ^t^ 3n/2 , - p c -R ^ v^ p c +R )

Пример 2. Составить внутреннее уравнение теоретической боковой поверхности цилиндрического косозубого колеса эвольвентного профиля.

Эвольвента является траекторией точки, принадлежащей прямой линии (производящей прямой), которая перекатывается без скольже- ния по окружности. В цилиндрических зубчатых передачах именно передачи с эвольвентным зацеплением распространены наиболее широко. Это является следствием их достоинств – нечувствительность передаточного отношения передачи к изменению межосевого расстояния, простота инструмента для обработки эвольвентных зубьев методом обкатки [8, 9, 10].

Уравнение эвольвенты и ее свойства обычно описывают в полярной системе координат. Ось 0 проводят через начальную точку эвольвенты. Положение точки на эвольвенте в полярной системе координат задают с помощью двух параметров – радиус-вектора и угла между радиус-вектором и полярной осью.

Уравнение эвольвенты ry =        , cosay invay = tgay - ay где ry – радиус-вектор текущей точки эвольвенты;

a_y – угол между радиус-вектором и полярной осью;

r_b – радиус основной окружности;

inva_y – полярный угол текущей точки эволь-веты (инвалюта угла профиля).

Эвольвента обладает двумя важными свойствами:

• 1.    Прямая, образующая эвольвенту, нормальна (перпендикулярна) к эвольвенте (и каса-тельна к основной окружности по условию образования эвольвенты).

• 2.    Радиус кривизны эвольвенты равен отрезку нормали от точки эвольвенты до точки касания нормали с основной окружностью.

Теоретической поверхностью косозубого эвольвентного колеса является поверхность, касательная к винтовой линии. Сечением такой поверхности плоскостью, перпендикулярной к оси цилиндра винтовой линии, будет эвольвента окружности сечения цилиндра этой плоскостью. Следовательно, такую поверхность можно получить винтовым движением эвольвенты относительно оси цилиндра, или погружением эвольвенты в конгруэнцию винтовых линий постоянного шага. Рассмотрим этот случай образования поверхности.

Совместим одну из торцевых плоскостей колеса с плоскостью xOy пространственной системы, ось основного цилиндра направим вдоль оси Oz. Тогда уравнениями конгруэнции винтовых линий, являющихся траекториями движения точек эвольвентного профиля, будут уравнения (9). Точки профиля, которые находятся в плоскости xOy, определяются значением параметра u=u0 и полярными координатами r=a+v, w с полярной осью Ox. Следовательно, внутреннему уравнению искомой поверхности будет со- ответствовать полярное уравнение эвольвенты окружности основного цилиндра, которое возможно получить из общих параметрических уравнений эвольвенты окружности радиуса а:

x = a (cos ф + ( ф - ф ₀) sin ф ), y = a (sin ф - ( ф - ф ₀) cos ф ) ,

где: ф , ф 0 - соответственно угловой параметр текущей точки окружности, которая поворачивается, и угловой параметр начальной точки эвольвенты. Подставим правую часть уравнений (12) в формулы перехода от прямоугольной к полярной системе

Р = ± 7 x1 + у2 = ± а^ (ф - ^0)2 + 1

y w = arctg — =

x

= arctg

' sn p - ^ - ^ )cos p' _v cos ф + ( ф - ф ₀ ) sin ф ^

Решив первое из уравнений относительно ф, учитывая, что r=a+v, и подставив его во второе уравнение, получим:

. ,    , ( v + a ) 2

sin⁽ P o ±i  --- T^^- 1) ⁺ a ²

( V + a ) 2 a ²

w = arctg

I

cOs( P o ±

( v + a ) 2 a ²

- 1) o ±

_л , ( v + a ) 2

- 1cos( p ₀ ±_A     ^-1)

a ²

1W-1 sm(R ± ((v+< -1) a                 a a > внутреннее уравнениt эвольвентного геликоида. Положительное или отрицательное значение двойного знака определяет направление развертывания окружности. На рисунке 2 дано изображение боковой поверхности зуба вместе с основным цилиндром.

Рис. 3. Поверхность цилиндрического косозубого колеса эвольвентного профиля

Как видно из рисунка 3, винтовые лиинии располагаются параллельно линии зуба, что несомненно является положительным результатом исследований, которое можно рассматривать с точки профилирования зубчатых колес.

ЗАКЛЮЧЕНИЕ

Полученные результаты указывают на то, что выбор первого или второго варианта координации пространства влияет на схему образования винтовой поверхности: уравнениями (6) удобнее пользоваться при винтовом движении плоской линии, плоскость которой проходит через ось движения, уравнениями (9) – когда ее плоскость перпендикулярна к этой оси.