Построения ассиметричных дельта - функций

Представление модели построенной с помощью дельта-функций открывает широкие возможности в изучении происходящего процесса описывая его как непрерывная функция от аргумента. Здесь кривая описывающая процесса представляется суммой нескольких дельта-функций. Для каждого процесса особый подход при выборе дельта-функций.

Методы построение дельта - функции Дирака, приведенные в [1,5] основном симметричны. Для построение асимметричной дельта - функции Дирака возьмём функцию ^ ( x ) , от который требуется только обращение в нуль при x = ±^ и отличие от нуля интеграла I = j ^ ( xdx . Всегда можно сделать этот интеграл равным 1, умножая ^ ( x ) на соответствующую константу. Если это предположить, тогда j ^ ( x de = 1 . Для простаты рассмотрим такие p ( x ) , которые имеют единственный максимум в x <=( -<» , да ) .

И пусть этот максимум достигается в точке т0 т.е ф(mо)- max^(x). Для хе(-»,и)

несимметричности функции р x ) достаточна добавить условия:

m о-л j ^( x dx / । ^( x dx(1),

-л другими словами площадь начертанный графиком  ^( x) x е(-л, m0) не совпадает с площадью ^( x) x е(m0, л).

Из выше сказанных условий попробуем построить функцию. Если  ^(x)  имеет единственный максимум значит ^ / (x) - 0 имеет единственное решение. Для начала просмотрим известную функцию рx) - е-х2 и действительно ^ / (x) - 0 имеет единственное решение при x - 0 т.е. т0 - 0. Проверим дополнительное условие (1), так как m'е-х2dx -jе-х2dx мы -л          т 0

конкретно не можем сказать что функция    ^ ( x ) - е ^х 2 не симметрична.

Чтобы выполнялось условия (1) будем искать функцию вида ^(x)- е х2к+x (где к целое и к>1) и действительно ^ / (x)- 0 имеет единственное решение при x - 2k-JX  т.е. т - 2kJX  и действительно если проверить условия (1)

2k              0      2k m ехр(- х2 к + xdlx /j ехр (- х2 к + xdlx     с помощью графиков     функций вида

-л                       т 0

р x ) - ехр - х ² к + x )   (где к целое и к >1).И так мы построили функцию вида

^ ( x ) - е ^{х + x} (1) и она удовлетворяет вышеуказанные условия.

Теперь нам остаётся добавить параметр n и построить дельта функцию и это видно из следующих графиков

М ^{x )-} lim n v ^{( nx} )    (2) [1] .

п ^л

4 x ) - lim пе - " >‘ ' ⁺ ” ^x       (3)

n ^л

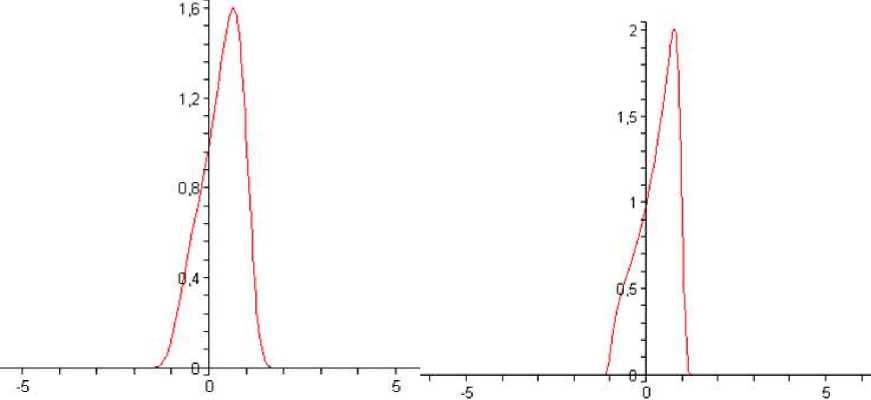
k=2, S = 2.1, m 0 = 0.63             k=5, S = 2.2, m0 = 0.85

Рис. 1. График функции (1)

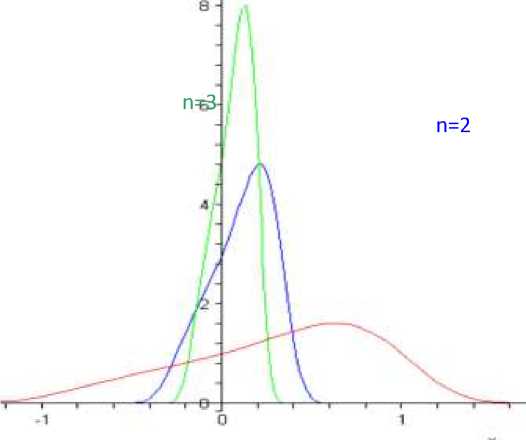
рис. 2. График функции (1) при различных n

Если анализировать построение несимметричных дельта – функций нетрудно заметит, что в функцию p ( x ) = е - х ^{+ x} в место x ² k можно поставить другую функцию потребовав положительность, посвей числовой прямой и более резкое возрастание относительно линейной функции. Например, показательная функция с основанием больше единицы.

Вывод

Учитывав что, из часто используемых показательных функций является экспоненциальная функция е^х можно построить несимметричную дельта-функцию виде ^ ( x ) = е ^{- е + x} (4).

Этот метод построение дельта-функций даёт широкую возможность в построении подходящего модели происходящего процесса