Потенциал взаимодействия атомов кремния

В настоящее время большой интерес в науке уделяется технологиям синтеза наноструктур различных материалов. Большую значимость для проектирования и прогнозирования конкретных видов структур представляет компьютерный эксперимент, основанный на численном решении уравнений движения частиц системы при известном потенциале их взаимодействия. Однако сегодня не до конца ясны природа и характер межатомного и межмолекулярного взаимодействия [1]. Например, атомы углерода могут образовывать множественные ковалентные связи с соседними атомами в решетке. Именно учет характера гибридизации в соединениях углерода приводит к сложности вывода формулы оптимального потенциала межатомного взаимодействия.

В данной работе предпринята попытка численного моделирования атомов кремния, являющегося одним из широко используемых химических элементов. Кремний по химическим свойствам схож с углеродом, но ему свойственна степень гибридизации sp3, благодаря чему атом кремния в кристалле может образовывать ковалентную связь с четырьмя ближайшими соседями [2]. Поэтому, ограничившись в первом приближении потенциалом двухчастичного взаимодействия атомов кремния, будем искать его как сумму двух составляющих:

V(r) = V ковал (r) + V B-B (r),                                                   (1)

Е.И. Герман, Ш.Б. Цыдыпов, В.Н. Парфенов, А.А. Гладких. Потенциал взаимодействия атомов кремния где Vковал(r) характеризует энергию ковалентного взаимодействия, VB-B(r) – потенциал вандерваальсового взаимодействия.

Для задачи подбора потенциала ковалентной связи вполне применим трехпараметрический потенциал Морзе [3], имеющий вид:

V ковал (r) = ε (e^-2α(r-σ) – 2e^-α(r-σ)),                                                              (2)

где ε = 52400 K – глубина потенциальной ямы, σ = 2.22 Å – расстояние, на котором потенциал имеет минимальное значение, α = 1.1 – подгоночный коэффициент.

Очевидно, что параметр ε определяет энергию, которую должна иметь частица, способная преодолевать притяжение других частиц в системе. Эта энергия рассчитывалась исходя из данных по удельной теплоте испарения кремния. Кристалл кремния имеет алмазоподобную кристаллическую решетку с периодом 5.43 Å. Параметр σ в (2) рассчитывался как ближайшее расстояние между атомами в кристаллической решетке, подгоночный коэффициент α – исходя из данных по пределу упругости и модулю Юнга кремния. Если механическое напряжение не превышает предела упругости, то, согласно закону Гука, зависимость приложенного напряжения от относительного удлинения должна быть линейной. Аналогичный характер должна иметь зависимость силы взаимодействия двух атомов в кристаллической решетке от расстояния между этими частицами. Интегрируя линейную функцию зависимости такой силы от расстояния, определяем вид потенциала вблизи его минимума:

„с

*^(г) = к — +f,                              (3)

где k = 40.18∙10-10H.

Потенциал имеет вид параболы в пределах 0.936σ ≤ r ≤ 1.064σ. Варьируя подгоночный коэффициент α, можно получить форму потенциала с ямой, схожей с функцией V упр (r) (рис. 1). Считая потенциал взаимодействия для ковалентной связи V ковал (r) короткодействующим, используем его в пределах первой координационной сферы, т.е. только для четырех ближайших соседей частицы кремния.

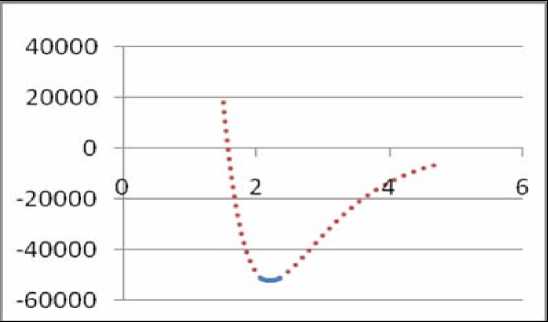
Рис. 1. Пунктирная линия – ковалентная составляющая потенциала взаимодействия атомов кремния, сплошная линия – кривая, рассчитанная с учетом упругих характеристик кремния

Для описания вандерваальсового взаимодействия нами использован известный двухпараметрический потенциал Леннарда-Джонса [4]:

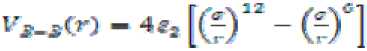
Параметр ε 2 на порядок меньше ε , входящего в уравнение (2) для потенциала ковалентного взаимодействия, так как вандерваальсовы силы значительно слабее сил химической связи. Путем подгона под температуры плавления и испарения в ходе компьютерного моделирования методом молекулярной динамики для атомов кремния было определено значение ε 2 = 0,08 ε .

В ходе моделирования системы атомов кремния методом молекулярной динамики были получены графики радиальной функции распределения, определяющей структурные характеристики вещества [5]. На рис. 2 представлены графики радиальной функции, соответствующие различным фазовым состояниям кремния.

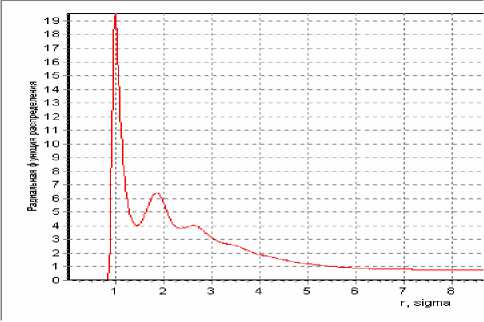
Рис. 2. Графики радиальной функции распределения кремния: а) жидкого при температуре 2000 К и концентрации 2*1028 м-3; б) газообразного при температуре 3000 К и концентрации 1*1028 м-3

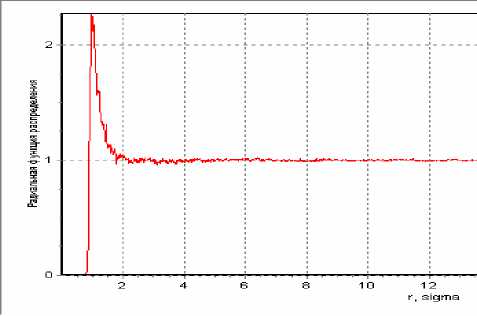
Таким образом, подобран потенциал, позволяющий описать взаимодействие атомов кремния. Данный потенциал довольно прост в вычислениях и применим к моделированию фазовых переходов кремния.