Потенциальная разрешающая способность оптико-электронного прибора космического базирования

На борту космических аппаратов (КА) оптико-электронные приборы (ОЭП) совместно с системой обработки информации (СОИ) являются основными информационными элементами систем управления движением и навигацией (СУДН) или дистанционного зондирования земли (ДЗЗ).

Во входящих в СУДН датчиках блока определения координат звезд семейства (БОКЗ) используются в качестве фотоприемных устройств отечественные ПЗС-матрицы «Лев» и «Сфера-1000» [1]. Отдельные основные параметры этих ПЗС-матриц приведены ниже (см. табл.).

Развитие звездных датчиков ориентации неизменно идет по пути повышения помехозащищенности приборов к воздействию внешних факторов, увеличения точности измерений при снижении массогабаритных и энергетических параметров. Одновременно перечисленные параметры звездных датчиков ориентации должны соответствовать требованиям конкретных типов изделий космической техники. В по-

следнее время не произошло событий, радикально изменяющих подходы к построению звездных датчиков ориентации. Так, например, для наблюдения звезд отсутствует необходимость ухода из видимой и ближней ИК-областей спектра в какой-либо иной спектральный диапазон [1–3].

Основные параметры ПЗС-матриц «Лев» и «Сфера-1000»

Характеристика	«Лев»	«Сфера-1000»
Внешний вид ПЗС-матрицы
Размер фотозоны, пкс	512 × 512	1024 × 1024
Размер пиксела, мкм	16 × 16	16 × 16
Квантовая эффективность, %, не менее, на длинах волн, нм: 550	45	34
700	45	45
900	10	13

Выходная информация ОЭП и СОИ содержит координаты источников излучения искусственного или естественного происхождения (далее – источники), по которым производится построение ориентации КА или наводится бортовая аппаратура зондирования. При этом источник излучения должен быть по крайней мере разрешен, обнаружен и отселектирован от других похожих источников излучения искусственного (ложных объектов) и естественного (звезд, планет и других подобных им объектов) происхождения.

Процесс обнаружения, селекции и измерения параметров движения цели ОЭП носит ярко выраженный вероятностный характер. Причиной тому являются флюктуации излучений искусственных источников, помехи от фоновых (распределенных по полю зрения) и точечных естественных источников на входе прибора и его собственные шумы. В результате выходная информация ОЭП после обработки СОИ выдается в СУДН с некоторой погрешностью, определяющей качество информационного обеспечения СУДН КА.

Исходя из вышеизложенного оценим значение такого основного показателя качества информационного обеспечения СУДН, как разрешающая способность ОЭП c ПЗС в диапазоне 0,1–1,0 мкм.

Оценка потенциальной разрешающей способности ОЭП

Очевидно, что разрешающая способность ОЭП зависит:

• –    от эквивалентной весовой функции оптической системы (ОС) и промежуточных звеньев (электронно-оптического преобразователя), характеризующей пространственные искажения, вносимые в оптическое изображение источника («размытие» точки в пятно рассеяния, или просто пятно);

• –    от растровой структуры матричного фотоприемника (МФП), характеризующей пространственные искажения, вносимые в электронное изображение источником (дискретизация по пространственным координатам оптического изображения).

Учет только первого фактора дает возможность оценить разрешающую способность при идеальном с точки зрения пространственной дискретизации приемнике

(пространственно-непрерывный приемник). При этом если рассматривается ОС дифракционного качества и предполагается отсутствие электронно-оптического преобразователя (ЭОП), то полученная оценка характеризует потенциальные возможности ОЭП по разрешению двух точечных источников (ТИ).

В материале данной статьи будет получено выражение, позволяющее оценить потенциальную разрешающую способность ОЭП с учетом диапазона длин волн принимаемого излучения, и определено условие, при котором приемник можно считать пространственно непрерывным.

Общепринятым критерием разрешающей способности оптического обнаружителя является критерий Рэлея раздельного восприятия двух ТИ [4]. Он требует, чтобы максимум изображения (пятна рассеяния) одного ТИ в фокальной плоскости дифракционной ОС совпадал с первым темным кольцом в дифракционном пятне другого ТИ. Таким образом, минимальное угловое расстояние 0min в радианах между двумя ТИ определяется выражением

О min

1,22Х

где X - длина волны принимаемого от ТИ монохроматического излучения; d ₀ - диаметр входного зрачка ОС.

Полагая, что радиус первого темного кольца в дифракционной картине изображения ТИ р₀₁ = d _ТИ/2, где d ТИ - диаметр пятна рассеяния, (1) можно записать в виде

О min

^d ТИ

.

2 f'

Выражение (2) можно считать более общим, так как dТИ определяется исходя из конкретного вида весовой функции ОС. Для ОС дифракционного качества, например, dТИ

= 2,44 X f‘ dо      .

Запишем критерий (2) применительно к ОЭП. При этом необходимо учесть увели чение в ГОЭП раз изображения ТИ в его промежуточных звеньях:

О min

d _TO

ОЭП f ОЭП

где / О _ЭП — эквивалентное заднее фокусное расстояние ОЭП.

Следует обратить внимание на то, что формулы (1)-(3) справедливы, если пренебречь пространственной дискретизацией изображения растровыми элементами (волоконно-оптическими и микроканальными пластинами и МФП).

При наличии в ОЭК только ОС и пространственно непрерывного МФП потенциальная разрешающая способность может быть определена по формуле (1). Однако реально принимаемое излучение не является монохроматическим, а характеризуется диапазоном AX . Уточним критерий (1) для этого случая.

В [5] приводится выражение распределения освещенности в плоскости изображения ОС дифракционного качества при приеме излучения в конечном диапазоне длин волн X1 + AX при нижней границе, равной X1:

E(X!, АХ, р) = л2 d0 Х,+гАХт0 (Х)тф (X)EA х

16 f '² I х

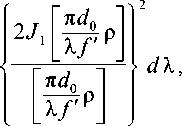
где р - полярный радиус в системе координат, связанной с центром пятна рассеяния; т _о( Х ), Т ф ( Х ) - спектральные коэффициенты пропускания оптики и фильтра; Е А _Х - спектральная плотность освещенности, создаваемая источником излучения на апертуре ОС;

J 1 - функция Бесселя первого рода первого порядка.

Если усреднить спектральные характеристики Е А _Х , т _о( Х ), Т ф ( Х ) (заменив их соответственно на E A _X ,т_о,Т ф ) по диапазону АХ , то, вынеся их за знак интеграла, получим вы-

ражение

E (X_PAX, р) =

^Л d 0 Т₀Т_ф E A _х

16 f '2

X 1 + ДХ

f

X 1

2 ( ^ ^J

4 J ¹ I X f' ^р \

-7 ^k      2 ⁷ d X .

X Г л d0 J

I 0 Р I k X f )

л d 0

Делая замену t = т— 77 р , преобразуем интеграл в выражении (5): ^{X f}

2 Г ^{Л d} 0 J

^X 1 + ^ДХ      J 1 !л Р г I                  /V t 2

f 4 -f- d x=-f 2 X1 X2 Г лd0 Y         л d0 Р t k X f'р )

J ( t )

Найдем неопределенный интеграл    ——dt :

t ²

J 1 ² ( t ) t ²

dt

.

f J^ dt = -f j2( t) d (1)=- j2( t) (1)+f td [ j2( t)J =

= 2 fl J,(t) Г J0 (t) -1JX t) 1 dt = - J2 (t) 1 + 2 f 1J, (t) J0( t) dt - 2 f ^ dt, J t L t J                 t j t                      t t где J0 - функция Бесселя первого рода нулевого порядка, т. е.

J ₁²( t )       2 1                     1 J ₁²( t )

f -^ dt = 3 f—Ji( t)Jо(t) dt- 3

Интеграл f-J (t) J (t) dt можно найти, используя выражение f1/ (az~)J (az)dz = t 0

Jц-1(аz) Jv (az) - Jц (az) Jv-1(az) Jц (az) Jv (az) r301 - ц -vц+v

J tJ 1 ( t ) J 0 ( t ) dt = tJ 2 ( t ) - tJ 1 ( t ) J - 1 ( t ) - J 1 ( t ) J 0 ( t ) .

Заменяя J _-1( t ) на - J , ( t ) согласно выражению J n ( x ) = ( - 1) n J - n ( x ) [31], получим

J 1 j 1 ( t ) J 0 ( t ) dt = tJ 2 ( t ) - tJ 1 ( t ) J - 1 ( t ) - J 1 ( t ) J 0 ( t ) .

Jt

Тогда интеграл     1-— dt будет равен:

t ²

f

JM dt.1 t^{2 dt} 3

2 tJ 2 ( t ) - 2 J , ( t ) J 0 ( t ) + Г ^ t ²-^-! J J 2 ( t )

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

Возвращаясь к выражению (5) и учитывая (6) и (7), можем записать:

E(X _p AX ,p)

^Л d 0 ^Т о ^Т ф E A x

12 f 'p

I 222      I .

2 tJ o ²( t ) - 2 J i ( t ) J o ( t ) +1         I JXt )

t 2 t ₁

или окончательно

E (X j , A X, p) =

^{Л d} О ^E A X ^Т ф ^Т о 6 f 'P

, f1

V

^л d о ) X1 f '^P )

—

,    л d f 1 -------------P f V (X1 + AX) f P

где f 1( z ) =

(2 ² OS'- .

------- I J 2 ( z ) + zJl( z ) - J 1 ( z ) J ₀( z )

I ^z J

Полученное выражение позволяет рассчитать освещенность в пятне рассеяния дифракционной ОС с учетом диапазона принимаемого излучения, но не дает возможности в явном виде выделить соответствующую весовую функцию. Преобразуем

л d_n формулу (8), сделав замену k =    ⁰ :

i_'_i

E ^(X i , ^{A X},^p) = Л d g E A x Т ф т 6               k p

f 1

| k p

V ।

— f 1 | — ^k—

V Xi + AX I

Рассмотрим функцию

f 3( k ,p, X) = -1- f I k p

^ I = ¹ J 2 1 k p I ^X J 2 ( k p X ^J X ¹ V X I 2( k p)^{2 1} V X

.1 2^ , k p 1_ ¹ T | k p 1 T ( k p 1 ⁺ A ^J 0 । A । у ^J 0 I A । ^J 0 I A | .

X V X | k p V X у V X у

Найдем lim f 3( k, p,X) , определив пределы каждого из слагаемых функции р, 0

f 3( k , p,X):

1) lim J 1 ² p ' 0 X

, k p 1V т I

= |lim J 1 1 kp J = I J 1 ²(0) = 0;

X p ' 0    V X у X

2) lim p'0

^X    2^ ¹ kp ¹

J

2( k p)² 1 V X ^J

используя выражение

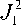
--lim

2 X p ' 0

J ( x )     ₁                      1

p imm "^r = 2 nn ! , будет равно ^— ;

^{p x}                            8X

3) lim J ²

’ pmo X ⁰

k p I

TJ

= ¹ lim J ²

X p m o ⁰

k p I

J

= ¹ J ²(0) = ¹ ;

X 0 X

4) lim pm0

по правилу Лопиталя

[ J o ( ^x ) J 1 ( ^x ) ] = J 0 ² ( ^x ) ^— x J 0 ( ^x ) J 1 ( ^x ) ^— J 1 ² ( ^x ) = 2

— lim k pm0

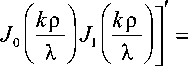
1 | k p I

2k V J

—

•

2 X

Таким образом, можем записать:

lim f 3( к , р,Х) = 1 -   - 1- = 3- = f 3( к ,0, X).

р — о             X 8 X 2 X 8 X

Используя (10), найдем освещенность в центре пятна рассеяния, определяемого выражением (9):

E (X_p A X, 0) = 6 к² d 2 E a x т_фт₀ [ f 3( к , 0, X , ) - f 3( к , 0, X , + A X) ] =

= 16 k d 0 E A X ^Т ф^Т<

—

X 1 X 1 + AX

¹  2 2^ — — ^{A X}

=— k d E т т ---------.

16     ⁰ A ^{X ф} ° X 1 (X 1 + AX)

Весовая функция теперь может быть найдена так:

%ифр ^(X 1 , ^AX, р)

E (X_P AX, р) E (X 1 , AX, 0)’

Окончательное выражение для весовой функции ОС дифракционного качества с учетом диапазона длин волн принимаемого излучения имеет вид:

W дифр (X_p AX, р) = ^8X 1 ( ^{X 1} + ^AX) [ f 3( k , p, XJ - f 3( k , p_sX₁ + AX) ]       (11)

или

^ дифр ^(X 1 , ^AX, р) =

8X 1 (X 1 + AX) f* 3 л d ₀ р AX

^л d о р ) Г ^л d о р ) f ' X 1 ) f ( f '{X 1 + AX} )

Рассмотрим поведение w _ди ф _р(Х_р AX , p) при уменьшении диапазона AX , другими словами, найдем w ^ ^(X_P 0, р) = ^l i m_o w дифр ⁽Х_Р \ + М, р):

W дифр (X, X + AX, р) = ^{8X (X} + ^AX) [ f 3( k , р, X) - f 3( k , р, X + AX) ] =

3(X + AX - X )

8         f3(k ³( ^k ’ р’ X + AX) - f 3( k , р, X)

= (X + X AX)

3                       A X

То есть

^ дифр ^{( X} ,0, р) = lim w дифр

AX—> 0

8X²      f3( k , р, X + AX) - f 3( k , р, X)

^(X,^{X + AX},^р) =^- IX аЬ-----------a ------------=

[ f 3( к , р, X) ] x

1 2 Г ^k р )

3 J ¹ ( X J

2 ( к р)²

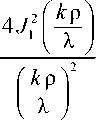
= ^ дифр ⁽р)"

= --3-[ f 3(kк , р, ^X) ] X

Таким образом, при сужении границ диапазона длин волн принимаемого излучения w _ди ф _р( Х ] , AX , р) стремится к весовой функции ОС дифракционного качества, определяемой выражением (13):

^ дифр ⁽X , р ) =

2 J_x I       р

11X f л dn —0 Р X f

.

Увеличение диапазона Δλ от нуля приводит к все большему рассогласованию весовых функций (13) и (11), которое можно оценить функцией разности следующего вида:

A W (X, AX, р) = | W д _И ф _p (X, X + AX, р) - w д _И ф _р (X + a AX, р) [            (14)

В выражении (14) весовая функция (13) записана как функция двух переменных: полярного радиуса ρ и длины волны λ + a Δλ , где а – некоторый коэффициент, имеющий значение в пределах от 0 до 1. То есть с помощью функции разности (14) можно оценить ошибку использования вместо w _дИ фр (Х_р АХ , р) весовой функции w _дИ фр ( Х , р), определяемой выражением (13), в которой диапазон Δλ подменяется некоторой эквивалентной длиной волны между нижней λ ₁ и верхней λ ₁ + Δλ границами диапазона (конкретное значение определяется коэффициентом а ).

На рис. 1 приведено максимальное по полярному радиусу ρ значение функции разности Δ W ( λ , Δλ , ρ ) при а = 0,5, изменении нижней границы диапазона (абсцисса графика) от 0,2 до 1 мкм и разности между границами диапазона Δλ от 0,1 до 0,5 мкм. Легко заметить, что только в области, близкой к 1 мкм, и при достаточно узких диапазонах ошибка не превышает 1–5 % . В ультрафиолетовой и синей части видимого диапазонах ошибка достигает уже десятков процентов.

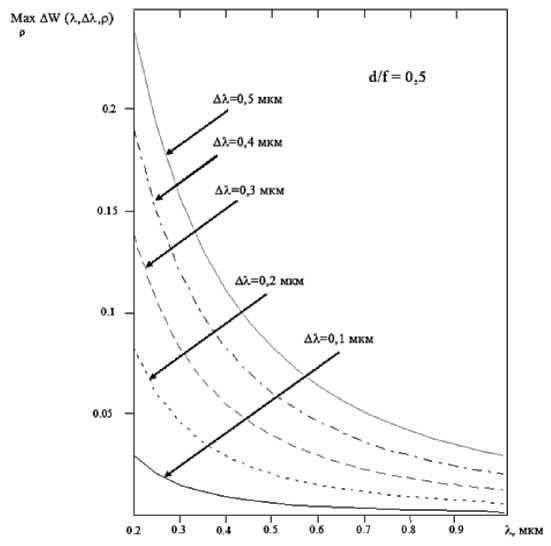
Рис. 1. Максимальное расхождение весовых функций ОС дифракционного качества в зависимости от диапазона длин волн принимаемого излучения

В отличие от весовой функции (13), w _дифр( λ ₁, Δλ , ρ) не имеет нулей, и оценку радиуса пятна рассеяния целесообразно производить по энергетическим соображениям.

Для ОС с весовой функцией (13) часть ΔΦ полного энергетического потока, падающего на круг радиусом ρ ₀, определяется выражением [6]

2 ( л d I _т2 ( л d I

^{АФ (}Р о ) = 1 ^- J o l T^—7^po ^- J 1 1 W^o .                    ⁽¹⁵⁾

V X f   7    V X f 7

В пределах первого темного кольца дифракционной картины, например, ΔΦ = 0,838. Найдем выражение, аналогичное (15), с учетом диапазона Δλ . Согласно выражениям (15) и (4),

X 1 + AX

АФ (Х_1; AX, р о ) = E ( _{х дх} ) • J т₀(Х)т_ф(X) Е_а х х

×

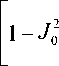
х f' ^р 0 7

л d 0

КГ ^р

d X ,

X i+AX где E(X1, АХ) = j т0(X)тф (X)Ea X dX — энергетическая освещенность, создаваемая

X 1

ТО на апертуре ОС в диапазоне Δλ с учетом искажений спектра, вносимых оптикой и фильтром.

Если вместо спектральных характеристик в формуле (16) взять их усредненные по диапазону Δλ значения, то, вынеся их за знаки интегралов, получим выражение

E      X 1 + AX АФ (X1, AX, p0) = —     J E (X i , AX) xJ 1	1 -	2f n d o_ n ^ J 0 11 Г'Ро V X f 7	т 2( Л d 0 _ - J 1 1 T"Fp о V X f    J_	d X .
Найдем неопределенный интеграл J	1 -.	2 (u^ ) 0 11 /V Po 1 V X f 7	_ T 2 f л d 0 - ) J 1 1 1 г' p0 1 V X f   7	d X:

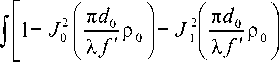
	замена
d X =	_ ^ d 0       k^ k 0 =      p 0 , z = A f        X	= J	T 2 1 k 0   |_ r2 | k 0   I       _ 1 J 01  1   1 J 1 |  1   I d X L V X 7 V X 7]

= ^X - k 0 J 2 ⁽ z )1 - ² k 0 j ¹ J 0 ⁽ z ) J , ⁽ z ) dz ^- ^ J / ⁽ z )1 + 2 k ⁰- f¹ J , ⁽ z ) J 0 ⁽ z ) dz = zz       3 z 3 z

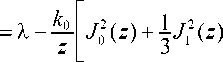
^- 3 k 0 J ZJ ^{1 (} z ) J 0 ⁽ z ) dz = ^{X -} Z

j 2 ( z ) + 3 j ²( z )

—

^- 3 k 0 { ^z [ ^J 0 ^{2( z} ) ^{+ J} 1 ^{2( z} ) ] ^{- J} 1 ^{( z} ) ^J 0 ^{( z} ) } =

_{X -}Г X² + 4/3 k 0 ² / J ₂

V X J0

X

< X² + 4 k ₀ ^{2 Л}

V 3X ₇

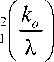
⁺ 3 k 0 J 1

f k^.)

VX J

J 0

f ko. )

VX 7

Подставляя полученное выражение в (17) и учитывая, что E(X1; AX 2) = Ea xAX , получим:

A Ф (X₁, AX, р о ) = 4• [ f 2(X_x + AX, p o ) - f 2(X_P р₀) ] ,            (18)

AX где f 2(X, ро) = X

f X ² + 4/3 к ₀ ² ) ₂

J

( X ) ⁰

k о ) _ ( ^{X 2 + 4} k о X , ,     3 X ,

J 2 1    | + ⁴ к 0 J 1

\ X ) 3

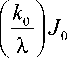
k ⁰ ) . X )

k ₀ =

^л d 0 Р о f'

Как и в случае с весовыми функциями, можно показать, что при уменьшении АХ до нуля выражение (18) преобразуется в (15). Степень же расхождения результатов, получаемых с помощью формул (15) и (18), можно охарактеризовать функцией разности радиусов пятен рассеяния следующего вида:

Ар(А Ф , X, AX) =

| p(X, X + AX, А Ф ) _ p(X + a AX, А Ф )| 100% p(X + a AX, А Ф )               °’

где р ( Х , Х + АХ , АФ ) и р ( Х + а АХ , АФ ) - функции, вычисляющие значение радиуса пятна рассеяния при заданном энергетическом пороге АФ , т. е. обратные функциям, представленным соответственно формулами (15) и (18). В явном виде их получить затруднительно, поэтому необходимо использовать для их вычисления методы последовательных приближений. На рис. 2 представлена зависимость функции разности (19) от диапазона длин волн принимаемого излучения при нижней границе Х = 0,3 мкм и пороге, изменяющемся в пределах 0,8...0,95.

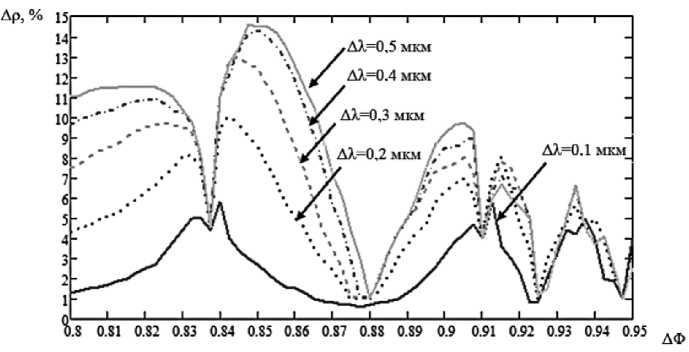
Рис. 2. Функция разности радиусов пятен рассеяния при различных значениях порога для нижней границы 0,3 мкм

Из рис. 2 следует, что ошибки применения формулы (15) для средней по диапазону длины волны могут достигать 15% в оценке радиуса пятна рассеяния. Рисунок также дает возможность выбрать значение порога, при котором ошибка минимальна, т. е. вместо формулы (18) можно использовать выражение (15). Одним из таких значений является энергетический порог, равный 0,877 (ошибка не превышает 1 % ). Можно показать, что порог 0,877 является оптимальным и для других значений нижней границы диапазона длин волн, а не только для 0,3 мкм.

При пороге 0,877 диаметр пятна рассеяния определяется выражением

, „ f ' (X. + A X/2) d _ти = 2,44 ^{7 v 1} ------

•

d о

Используя формулу (2), разрешающую способность оптической системы дифракционного качества с учетом диапазона принимаемого излучения определяют выражением

O mn = 1,22 ^^

d ₀

Как было указано выше, выражения (1)-(3), а следовательно, и полученное (20) справедливы, когда искажениями пространственной структуры изображения ТИ можно пренебречь. Теперь определим условие, при котором этими искажениями можно пренебречь.

Пусть ОЭП состоит из ОС и МФП и весовая функция ОС известна, причем она является изопланарной и осесимметричной:

Woc (x, У, x0, У о) = woe (x - x0, У - Уo) = woe ( p), где x, у - координаты точки плоскости изображения ОС в прямоугольной системе XOY с центром в осевой фокальной точке ОС; x0, у0 - координаты центра весовой функции; р = ^(x - x0 )2 + (у - у0 )2. Для простоты в дальнейшем будем полагать, что x0 = 0 и У0 = 0.

Матричный приемник излучения является дискретной структурой. Координата в системе координат XOY (рис. 3) левой границы любого пикселя, находящегося в n -м столбце, будет определяться выражением

Xом + hg/2 + (n - 1)(lg + hg) при n > 0 xом + hg /2 + n •(lg + hg) при n < 0, правой границы - xnp n = xом - hg /2 + n (lg + hg X нижней границы любого пикселя, находящегося в m-й строке y н m

У ом + hv /2 + (m - 1)( lv + hv) при m > 0, при m < 0.

_ У ом ⁺ h v ^{2 + m (} l v ⁺ h v )

и верхней границы -

У в m = У ом ^- h v ^{/2 +} m ( l v ⁺ h v X

Введем растровую функцию следующего вида: можно пренебречь

A , еоли ( x <  x <  x ) и ( y <  y <  y ); л n           np n        н m ^y      в m

/                  x         ^J            v л n            np n ' Hm н m

X ( x , У , x ом , У см ) = ^

0, еоли уоловие не выполнено, где А - постоянный множитель. Для удобства будем полагать А = 1. Тогда весовая функция рассматриваемой структуры ОЭП будет следующей:

^ оэп ( ^x , У ) = Х ( ^x , У , ^x ом , У ом ) w oe ( ^x, У )•

Несмотря на то, что весовая функция ОС в соответствии с выражением (21) является изопланарной, w _ОЭП( x , у ) не будет таковой из-за наличия в (23) множителя Х( x , у , x _см, у _см). Однако при определенных условиях весовую функцию ОЭС можно считать изопланарной. Определим их.

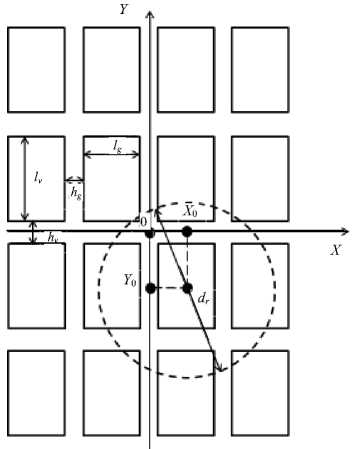
Рис. 3. Матричный приемник излучения

Согласно теореме отсчетов частота пространственной дискретизации w _ОС( x , y ) должна быть не менее удвоенной ширины ее пространственного спектра Δ w _ОС для неискаженного воспроизведения. Наибольший шаг дискретизации для МФП, представленной на рис. 3, составляет расстояние между серединами зон чувствительности смежных по диагонали пикселей. Фактически это длина диагонали пикселя d pix = ^ ( l g + h g )² + ( l v + h v )² . Тогда условие безыскаженного воспроизведения весовой функции ОС можно записать следующим образом:

— >  2 A w _oc.                          (24)

d pix

Ширина Δ w _ОС пространственного спектра весовой функции ОС зависит от ее конкретного вида.

Спектр весовой функции в виде гауссоиды вращения

W oc (p) = e ~^{Р 2/ ( 2 Р} 0 ) ,                                      (25)

где ρ ₀ - радиус пятна рассеяния на уровне 0,607, повторяет ее по форме с той лишь разницей, что вместо полярного радиуса ρ берется обратная ему величина - круговая пространственная частота u = (2 π )/ ρ :

h( u) = e - u2(2 u2), где u0 = 1/ρ0. Ширина спектра при этом равна:

^A ^ 0 = — .

P o

Тогда формула (24) для весовой функции в виде гауссоиды вращения примет вид:

d px ^ ^0,25P o -                                 (26)

Для ОС дифракционного качества с весовой функцией вида (13) ширина спектра

2 d

A w _ф = —0. Следовательно, условие (24) сводится к выражению _х f ,

Xf'

d < —.

pix 4 d

Ограничивая радиус пятна рассеяния ОС дифракционного качества первым нулем

^ f '

функции (13) р₀j = 1,22---, запишем (27) в виде

01           _{d 0}

d pix <  0,2P ci -                                        (28)

Для весовых функций другого вида, имеющих бесконечный спектр, при ограничении его на уровне ~ 0,9 от полного объема, заключенного под поверхностью, описываемой формулой весовой функции, условие (24) близко к выражению (28). Например, для круговой весовой функции

" А ⁽ x , У ) =

1, если

0, если

2.2/  2

X + У <Р пр ,

2.2   2

X + У >  Р пр

условие (24) имеет вид d_pix ≤ 0,22ρ_пр, где ρ _пр - радиус пятна рассеяния.

Переходя от радиуса к диаметру пятна рассеяния и учитывая близость условия (24) к (28) для большинства весовых функций, получим достаточно общее выражение dpx 5 0,4dТИ.

Физически формулу (29) можно интерпретировать так. Весовую функцию ОС, ограниченную на плоскости аргументов квадратом, в который вписан круг диаметром d _ТИ, можно представить (оцифровать) в виде матрицы не менее 16 × 16.

Таким образом, если параметры системы не удовлетворяют условию (29), то при оценке разрешающей спо собности необходимо учитывать неизопланарность весовой функции рассматриваемой конфигурации ОЭП. При соблюдении условия (29) (или при необходимости оценить потенциально достижимое значение разрешающей способности) можно воспользоваться выражениями (1)–(3), а с учетом диапазона длин волн принимаемого излучения - (20).