Потенциальные границы пропускной способности дискретного канала связи, учитывающие стохастические свойства входящего в его состав непрерывного канала

Известно, что выбор того или иного критерия качества любой системы, в том числе и связи, является чисто субъективным, поскольку определяется наличием определенных требований со стороны разработчика, потребителя или любого другого субъекта. Однако для систем связи Шенноном введено понятие взаимной информации как меры определенности о сигналах на входе канала связи исходя из наблюдений о сигналах на выходе канала [1-2]. Причем данная мера имеет фундаментальный смысл, поскольку однозначно определяется лишь вероятностными характеристиками допустимых для передачи сигналов и канала связи, что является следствием несущественности дальнейшей интерпретации и использования переданных сообщений [3]. Кроме того, взаимная информация и производная от нее пропускная способность позволяют указать условия безошибочной передачи данных при наличии дополнительной последовательной обработки в виде кодирования и декодирования [4-5].

В общем же технический эффект систем передачи информации определяется количеством и качеством переданной информации [6-7]. При этом количество информации возможно рассматривать как произведение технической скорости передачи на время передачи. Поскольку канал связи по своей природе является стохастическим, то неизбежны ошибки в воспроизведении передаваемых сообщений. Доля подобных ошибок, а с позиции вероятностных мер – вероятность неточности воспроизведения, служит качественной характеристикой переданных сигналов. Совершенно естественно одновременная оптимизация систем связи по обоим показателям оказывается трудноразрешимой задачей не только вследствие их взаимообратной зависимости, но и просто из-за необходимости исследования векторного показателя качества. В результате существует объективная необходимость в использовании показателя, который одновременно учитывает количественную и качественную характеристики процесса передачи информации, имеет достаточно ясный физический смысл. Подобными свойствами и обладает введенное Шенноном понятие скорости передачи информации как взаимной информации, приходящейся на единицу времени передачи сообщения [8].

Однако и для данного случая существуют определенные трудности, связанные с невозможностью увеличения взаимной информации посредством дополнительной последовательной обработки передаваемых сигналов, что являет- ся следствием теоремы о переработки информации [2-3]. Например, использование любого корректирующего кода способно лишь снизить (в лучшем случае сохранить) скорость передачи информации по каналу связи [9]. В то же время их применение продиктовано требованиями к определенному уровню достоверности передаваемых сообщений, увеличение которого и достигается за счет снижения скорости передачи информации. Если же возникает необходимость в дальнейшей последовательной обработке получаемых данных, то «вернуть» потерянную взаимную информацию не представляется возможным без изменения свойств корректирующего кода. В этой связи следует отметить, что практически все существующие системы связи построены и проектируются по принципу универсальной модульности, что предполагает дальнейшую последовательную обработку информации как, впрочем, и предварительную. Например, корректирующие коды разрабатываются применительно к определенному дискретному каналу связи, которые, в свою очередь, являются дискретными отображениями непрерывных каналов связи.

Верхняя граница

В целом же взаимная информация учитывает конкретный вид распределения вероятности сигнала на входе модулятора, а следовательно, как показатель качества системы передачи информации характеризует не только канал связи как таковой, но и вероятностные параметры передаваемого по нему входного сигнала. С одной стороны это является существенным достоинством подобного показателя, поскольку позволяет синтезировать дискретные отображения, учитывающие дополнительную априорную информацию об источнике помимо информации о свойствах непрерывного канала связи.

С другой стороны возможность с помощью кодера источника и кодера канала варьирования статистических характеристик сигнала на входе модулятора может потребовать синтеза оптимальных отображений для всех возможных вариаций этих дополнительных априорных сведений. К тому же зависимость величины взаимной информации от характеристик источника может быть столь значительной, что в ряде случаев способна практически полностью нивелировать достоинства оптимальных отображений по отношению к неоптимальным.

Следовательно, существует объективная необходимость в анализе дискретных отображений с позиции некоторой потенциальной характеристи- ки, рассчитанной на произвольные статистические свойства источника. Подобным показателем, имеющим важный теоретико-информационным смысл, является пропускная способность [2-3; 10-12], определяемая как максимальное значение взаимной информации по всем возможным распределениям вероятности сигнала на входе модулятора:

С_х х' ~ max /_{х х}<, Ы_х ’

где ^Х,Х* – взаимная информация дискретного канал связи; (Ох(х) – распределения сигнала на входе модулятора; а индексы Сх,х' И ^Х,х' указывают на границы канала (дискретный), поскольку пропускной способностью и взаимной информацией так же могут характеризоваться и непрерывный, и дискретно-непрерывный, и другие каналы связи.

Вычисление же пропускной способности оказывается еще более трудоемкой процедурой, чем расчет взаимной информации, поскольку помимо многократного интегрирования согласно (1) следует проводить еще и оптимизацию по множеству распределений сигнала на выходе модулятора. Таким образом, и в данном случае следует указать границы, определяемые как свойствами исходного непрерывного канала связи, так и параметрами модулятора и демодулятора. Причем данные границы оказываются потенциальными, поскольку характеризуют предельно достижимые величины взаимной информации для заданного дискретного отображения.

Учет неравенства треугольника для метрики в форме максимумов тах(д + й) < тахд + тахб, а также равенства тах(- Л) = - min 6 позволяет ограничить пропускную способность неравенством [2]: X, X X X / X ^ где ^Нх'

сох сох А – энтропия сигнала на выходе демодулятора х';

Hx'lx – условная энтропия сигнала на выходе демодулятора x’ при известном сигнале на входе модулятора x . Так как верхняя граница энтропии сигнала на выходе демодулятора имеет вид [3]:

Нх-<\о^

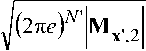
где 7V – размерность сигнала на выходе демодулятора х'; Мх;2 – ковариационная матрица сигнала на выходе демодулятора х'; |А| – определитель (детерминант) матрицы A, то очевидно, что тахЯх>< log сох

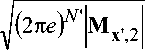
Поэтому граница пропускной способности принимает форму:

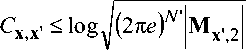
-min//xyx.   (2)

(0 х

Условная энтропия представляется в следующем виде [3]:

Нх^х -

= f co_x(x)j co_xy_x(x',x)log--------- ^Ях'Ях. (3)

X X' '              tox'/x(X'’X)

ЮХ'/х(х',х) – функция правдоподобия дискретного канала связи.

Очевидно, что условная энтропия линейно зависит от плотности вероятности сигнала на входе модулятора. Следовательно, ее минимум по этой плотности достигается в случае детерминированности данного сигнала x , причем его значения с вероятностью единица соответствуют минимальным значениям интеграла по области определения сигнала на выходе демодулятора х' в (3), то есть при следующем условии:

min Я_ху_х = min Г <в_ху_х (х¹, x)log------,----г Ях'.

«X           X х, '            СОхух(х',х)

Таким образом, в соответствии с (2) верхняя граница пропускной способности определяется выражением:

-тт

X

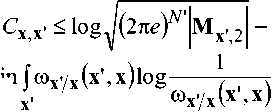
Ях'.

Нижняя граница

Нижняя граница пропускной способности вычисляется на основе неравенства согласно (1):

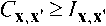
При этом естественно, что взаимная информация в данном неравенстве может быть рассчитана для произвольного распределения вероятностей сигнала на входе модулятора ЮХ ’ в том числе и для гауссовского, но с некоторой произвольной ковариационной матрицей Mx2. Умножение и деление выражения под логарифмом взаимной информации, взятой с противоположным знаком, на плотности вероятности некоторых многомерных гауссовских случайных величин z и y с плотностями вероятности coz и соу и ковариационными матрицами, определяемыми соответствующими выражениями:

Mz,2=Mx,2-2Mx,u1+MXi2,(5)

My,2=Mz,2+MX)2,(6)

где Mx'.l.x.l – матрица совместных моментов второго порядка сигналов на входе модулятора и выходе демодулятора, определяемая в форме

Mx-; x ; = f f cox' x x'.xk'W Vix’dx,(7)

A ^t ^ A ^ / J J A ^ A \ v \'

XX*

z

(декартово) произведение некоторых векторов X (символ «X », если не указано дополнительно, в дальнейшем обозначает прямое – декартово произведение). Форма исходного выражения при этом не изменяется:

^x',X J J®x'/x(x ,x)tox(x)x

COx^X^COy^'^O^x'-x) ,      (8)

xlog----z---г—^—-,--- -dx dx.

COx'/x (x', x)(Oy (x’)cDz (x'-x)

Применение свойства логарифма произведения и условия нормировки плотностей преобразуют (8) к виду:

^x',x — j f ®x7x(x ,x)cox(x) x , (Ох'Гх'^ВуГх'-х) , , , X lo g —x \ 7        dx’dx- coxyx(x' ,x)toy(x')

- jo>x'(x')loga)y(x')z/x'-

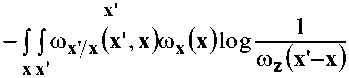
dx' dx.

Второе вычитаемое принимает форму:

J f(Ox'/x(x',x)a>x(x)log—-,----^dx'dx - xx'                     toz(x'-x)

=Ы2я)т|м;'/²|₊^       (10)

X J J co_xy_x (x', x)co_x (^x)(x'-xXx'-x)^r dx^ dx , xx'

где tr A – след матрицы A ; T – оператор транспонирования. Раскрытие скобок в подынтегральном выражении позволяет представить (10) в виде:

J J «x'/x (s', ^XH (x)!og z , x dx' dx = xx'                ^(x-x)

= log(2^-)T|M’/22| +

Таким образом, на основе (5) и свойства произведения обратной матрицы на саму матрицу второе вычитаемое (9) имеет форму:

xx' ___________________ ^COz

= log (2ке)^№М_х,₂-2М

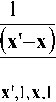
dx'dx =

+ Mx,2'

Первое же вычитаемое согласно (6) задается следующим выражением:

J tox' (x')log (Oy (x')(/x' = x’ _________________________________

= -^12716^^^2+MX,2.

Уменьшаемое (9) на основе неравенства -logx> (1 -x)loge после сокращения числителя и знаменателя дроби на одну и ту же функцию, а также учета условия нормировки для плотностей вероятности преобразуется к виду

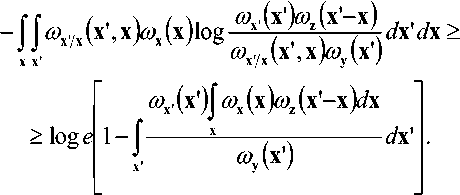
Поскольку для выполнения неравенства (4) распределение вероятностей сигнала на входе модулятора ®x может быть выбрано произвольно, то в случае гауссовского распределения на основе (6) и правила композиции двух законов распределения гауссовских случайных величин [13]:

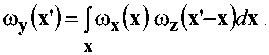
Сокращение числителя и знаменателя на одну и ту же функцию и учет свойства нормировки плотностей приводит на основе (13) к следующе- му неравенству:

-fjtox'/x(x',x)a)x(x)x

,    ®x'(x')coz(x'-x)    ,

X log — ^XVz⁷_x dx' dx>0.

юх'/х(х',х)(Оу(х')

Таким образом, подстановка (11) и (12) в (9), а также учет неравенств (4) и (14) и равенств (5) и (6) делает справедливым следующее неравенство:

^Сх',х - l°g^M_x, ₂^2Мх'Д,х,1 ^{+ 2М}Х,2 -10g^M_x,,₂ -²M_x,j_;x,1 ^+Мх,2 '

На основе свойств суммы логарифмов, а также равенства определителя произведения матриц произведению их определителей [14] нижняя граница пропускной способности принимает форму:

▻ log

Е₂+М ₂(м . 2 ^2Мх'|х1^+Мх2Г

Z^       А,^ \ Л ^^         Л ^1^Л^Х         Л^Д- )

где порядок единичной матрицы Ез равен порядку ковариационных матриц МХ-2, Мх’д,х,1 и Мх',2-

Таким образом, доказана нижеследующая теорема, задающая границы пропускной способности для произвольных непрерывных каналов связи и сигналов, передаваемых по ним.

Теорема о потенциальных границах пропускной способности

Пропускная способность дискретного канала связи, получаемого путем дискретного отображения произвольного непрерывного многопараметрического канала, ограничена следующим интервалом:

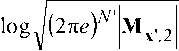
- min f со_ху_х(х', x)log------,----г dx> X _х' '             <»х'/х(^Х',^Х)

> с, >

▻ log Е2

/                         V1

+ Мх 9 Мх, 2 — 2М , J । + М 2 /

Следует отметить, что данная теорема является некоторым обобщением границ, полученных в [2], на случай многомерного дискретного канала связи, образованного на основе операторов модуляции и демодуляции с ограниченной степенью нелинейности.

Выводы

Таким образом, сформулированная и доказанная в работе теорема устанавливает определенные ориентиры, по которым возможно оценивать достоинства и недостатки конкретных операторов модуляции и демодуляции. При этом очевид- но, что существование явного оптимального вида дискретного отображения приводит к наличию еще одного ориентира для пропускной способности формируемого дискретного канала связи. Однако соответствующая этому оптимальному решению пропускная способность не всегда будет оказываться более точной верхней границей по сравнению с полученной, поскольку в данном случае оптимизация проводится путем варьирования только операторов модуляции и демодуляции без изменения распределения вероятностей сигнала на входе модулятора.