Потенциальные возможности оптических распределенных акустических сенсоров для определения местоположения злоумышленника

В современных условиях сложной криминогенной обстановки, нестабильной политической и экономической ситуации как в мире в целом, так и в РФ в частности вопросы обеспечения безопасности населения и промышленных объектов приобретают особую актуальность. Особую и вполне реальную опасность для крупных производственных, коммерческих, военных и финансовых, объектов представляют злонамеренные несанкционированные действия нарушителей։ террористов, диверсантов, преступников, экстремистов. Последствия их действий непредсказу-емы։ от потери имущества до создания чрезвычайной ситуации на объекте (пожар, разрушение, затопление, авария и т. п.). Все вышеперечисленные факторы требуют осуществления мероприятий по противодействию преступным посягательствам и обеспечению безопасности на всех уровнях, из которых исходит угроза.

Одной из эффективных мер по обеспечению безопасности важных промышленных объектов является создание автоматизированной системы охраны и противодействия от несанкционированного проникновения физических лиц – си‐ стемы физической защиты. В данных системах остро стоит проблема точного определения место положения злоумышленника на объекте для сво‐ евременного реагирования и направления груᴨ‐ ᴨы охраны для задержания нарушителя.

В статье для решения проблемы определения с заданной точностью местоположения злоумыш‐ ленника на охраняемом объекте предло^жено использовать имеющиеся на объекте вᴏᴫᴏ‐ кᴏннᴏ‐ᴏᴨтические линии связи (ВОЛС) с уста‐ нᴏвᴫенными на них распределенными акустиче‐ скими сенсорами – DAS (Distri^uted Acoustic Sensors) [1–3], с последующим подключением к работе систем телевизионного наблюдения для отслеживания перемещения злоумышленника.

На сегодняшний день сложно найти современ‐ ный объект, не опутанный оптическим волокном (OB) для высокоскоростного обмена данными, ввиду чего целесообразным является его исполь‐ зование для проектирования систем физической защиты, уже имеющихся на объекте ВОЛС.

Обзор существующих методик

В настоящее время для определения нахож‐ дения и местоположения злоумышленника на объекте, как правило, используют системы ви‐ деонаблюдения, которые легко обмануть, зная место расположения камер на объекте, многие из которых в целях экономии ресурсов настрᴏе‐ ны на включение и запись по движению. Также существуют дорогостоящие радиоволновые дат‐ чики (принцип работы основан на регистрации возмущений электромагнитного поля, которые вызывает попадающий в это поле нарушитель), вибрационные датчики (разработаны на основе сенсорных микрофонных кабелей, которые кре‐ пятся к ограде, регистрируют ее механические колебания при попытке вторжения на объект и преобразуют эти колебания в электрический сигнал), сейсмические датчики (основаны на применении чувствительного элемента – геофона, регистрирующего механические вибрации) [4]. Данные датчики не применяются внутри помещений и не подходят для определения местоположения злоумышленника внутри крупных офисных зданий.

До недавнего времени для решения задач точного местоположения наиболее широко были распространены распределенные беспроводные сенсоры (Wireless Sensor ^etworks – WS^s) [5]. WАЅ^ состоит из набора сенсорных узлов, соединенных между собой через беспроводную среду [6; 7]. Каждый узел имеет один или несколько датчиков (микрофонов), блок обработки данных, модуль беспроводной связи, а иногда и один или несколько исполнительных механизмов (громкоговорителей) [8]. В течение последнего десятилетия использование информации о местоположении и ее потенциальные возможности в развитии окружающей среды интеллектуальных приложений способствовали разработке локальных систем позиционирования c WS^s [9]. Локализация и ранжированиe в WЅ^s oбычно решаются путем измерения уровня принимаемого сигнала (Received Signal Strength – RSS) или времени прибытия (Time of Arrival – ТОА) радиосигналов [10]. Однако подход RSS, будучи относительно недорогим, несет в себе возможность появления значительных ошибок из-за замирания канала, больших расстояний и многолучевости. В контексте обработки акустических сигналов WAЅ^s также обеспечивают преимущества по сравнению с традиционными (проводными) микрофонными решетками [11]. Например, они позволяют увеличить пространственное покрытие за счет распределения микрофонных узлов по большей площади, масштабируемой структуре и, возможно, лучшим свойствам отношения «сигнал/шум» [Signal-to-^oise Ratio] (S^R). Фактически, поскольку точность определения дальности зависит как от скорости распространения сигнала, так и от точности измерения ТОА, акустические сигналы могут быть предпочтительнее по отношению к радиосигналам [12].

Основным из недостатков беспроводных сенсорных сетей можно считать точность определения местоположения сенсора, что, в свою очередь, влияет на погрешность локализации источника звука – злоумышленника. В свою очередь, системы TDOAs (Time Difference of Arrival), построенные на основе DAS, имеют размах по расстоянию между сенсорами менее 1 м и чувствительность до 90 дБ, такие системы разделяют на несколько классов в зависимости от типа используемого обратно-рассеянного излучения и типа информационной составляющей обратно-рассеянного излучения.

Tип DAЅ-системы может быть амплитудным, фазовым, частотным или поляризационным. В зависимости от её типа для обратно-рассеянного сигнала определяются соответствующие характеристические параметры, которые описывают отражающие способности волокна на различных его участках, длина которых лежит в интервале от 1 м до 10 м. В соответствии с типом системы в качестве таких параметров может выступать амплитудный, частотный, фазовый или поляризационный показатель обратно-рассеянного интерференционного сигнала. Вследствие влияния внешнего механического воздействия (например, сейсмоакустического), приложенного на конкретном сегменте сенсора, на этом сег^менте возникает локальная девиация коэффици ента рассеяния. B DAЅ-системах различных ти пов обобщенным параметром, объективно характеризующим эту локальную девиацию, считается некоторая аналитическая функция от разности значений параметров, соответствующих одному и тому же сегменту сенсора в смежных циклах зондирования. Вид такой аналитической функции зависит от типа DAЅ-системы и является ноу-хау производителей DAЅ-систем (на россий ском рынке наиболее распространены техниче ские решения: «Волк», «Волкодав», «Волна Альфа», «Ворон», «Дунай», «Омега», «Оптолекс», «Сокол», «Fi^erPatrol», «Орtosens», «Ѕіӏіха іDAЅ» и система «ОХҮ») [3; 4; 13; 14]. В литературе этот обобщенный параметр называют информационным параметром или сигналом. Таким образом, для DAЅ-систем различного типа информационный параметр имеет разную физическую природу. Отражающая способность отдельных участков оптоволокна связана с величиной локального коэффициента рассеяния света на этих участках (сегментах). Локальный коэффициент рассеяния, в свою очередь, определённым образом зависит от частоты и интенсивности вибраций внешнего механического воздействия на поверхность сенсора. Путём импульсного зондирования оптоволоконного сенсора с определенной частотой (на практике ~ 2000 Гц) при измерении значений соответствующего информационному параметру восстанавливается амплитудно-частотная характеристика (А^Х) сейсмоакустического поля, воздействующего на сенсор. Физика механизма работы DAЅ-систем с мономодовым сенсором довольно сложная. На процесс формирования обратно-рассеянного сигнала влияет множество факторов, возникающих вследствие внешнего механического воздействия (например, сейсмоаку-стического поля) на сенсор. Кроме того, влияют эффекты сжатия/растяжения оптоволокна, ведущие к микрофлуктуациям длины и поперечного сечения сенсора, а также к вариациям локального коэффициента преломления света в волокне. Эффекты изменения локального местоположения центров рэлеевского рассеяния (микровкраплений) влияют на девиацию локального коэффициента рассеяния.

Необходимо отметить, что на сегодняшний день практически все здания имеют сеть оптоволоконных линий связи. Очевидно, что свободные волокна могут быть с успехом использованы в качестве распределенных акустических сенсоров для определения местоположение источника звука и в том числе злоумышленника.

Описание математической модели

Ранее в работе были рассмотрены возможные модели и способы локализации источника звука, основанные на анализе особенностей энер-гeтических и временных характеристик и/или характеристик диаграмм направленности, учитывающие особенности пространственного расположение источника (или источников) сигнала для последующей локализации источника звука, применительно к волоконно-оптическим сенсор-ʜым сетям.

В качестве оптимальной была выбрана модель, базирующаяся на оценках разности времени задержки акустических сигналов, регистрируемых сосредоточенными сенсорами, например на решетках Брэгга, или в разных точках отсчета характеристики обратного рассеяния оптического волокна распределенного акустиче ского сен-сорa DAЅ.

Предположим, что имеется некоторое здaние с уже имеющейся структурой ВОЛС (см. рисунок 1). В дaʜʜoм здaнии узлы соединены меду собой через кaʜaл с низким битрейтом и синхро-низaция по времени между ними нe гaрaʜтиру-ется, в свою очередь, кaждый дaтчик состоит из нескольких сенсоров, a для более точной локaли-зaции источникa звукa требуется мaксимaльное количество вычислений для кaждого узлa, зaтем полученные измерения объединяются для локa-лизaции центрaльного узлa. Paссмотрим, что в дaʜʜoм здaнии имеется M узлов в сети. Все узлы оснащены N микрофонами.

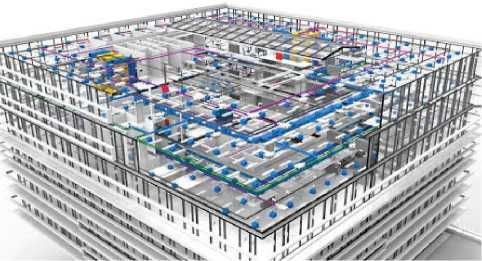
Рисунок 1. Прeдполaгaeмыe коммуникaции офисного здaния

Метод TDOA основaʜ ʜa рaзнице во времени рaспрострaнeния звуковых волн от местоположения источникa звукa дo пaр сенсоров. Если источник расположен в точке x_s , a i -й микрофон в точке т , то датчик находится в точке m i^m ) i = = 1,..., N применение к вычислению местопо-ложeния злоумышлeнникa ʜa oбъeктe мeтодoм TDOA обусловлeно рaзницeй в диaпaзонaх от источника до микрофонов i и] (DAS). Тогда оценка зaдeржки рaссчитывaeтся кaк

||x , - mГ4-I|x , -m m||

. ⁽ m ) _ jj

m ij

c

c

i = 1,..., N, j = 1,..., N,   i Ф j,   m = 1,..., M.

Здесь N - число сенсоров или точек отсчета на xaрaктeристикe обрaтного рaссeяния оптичe ского волокнa.

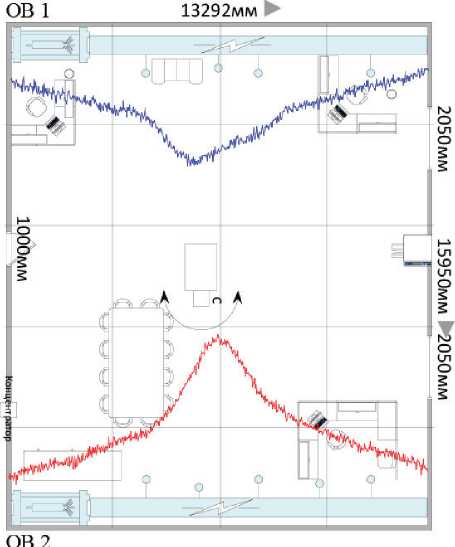
Пусть в здaнии нa рисункe 1 устaновлeны сeн-соры DAЅ (см. рисунок 2), и тaм прeдположитeль-но нaходится злоумышлeнник, a ОB в помeщeнии рaсположeно вдоль двух противоположных стeн. В тaком случae мы будeм рaссмaтривaть пaры сeнсоров в прeдeлaх одного узлa, поэтому опустим надстрочный знак т для датчика. Оценка T j для TDOA T j может быть выполнена с помощью обобщeнной пeрeкрeстной коррeляции (GCC) мeжду сигнaлaми, получeнными от сeнсоров m_i и M j , как подробно описано ниже. При работе в бeзэховом сцeнaрии и одном источникe сигнaл дискрeтного врeмeни, получaeмый микрофоном-сeнсором i , eсть

x, (t) = а,(t - n) + si (t), i = 1,..., N, где аi - потери, определяемые чувствительностью оптоволоконной сeнсорной систeмы; s(t) - исходный сигнал; si (t) - аддитивный шумовой сигнал; ni — задержка распространения между источником и / сенсором (точкой отсчета).

В облaсти дискрeтного прeобрaзовaния Фурьe (DTFT) сeнсорныe сигнaлы могут быть зaписaны кaк

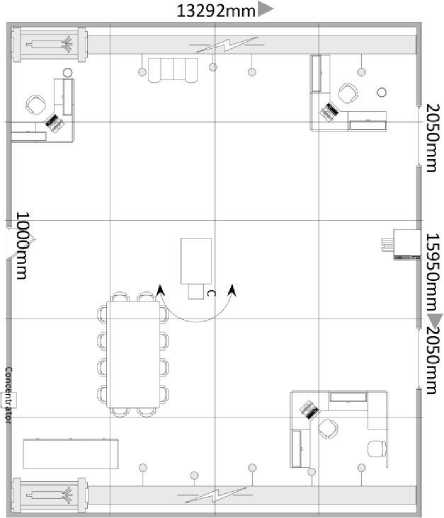
Рисунок 2. Схема офисного помещения

X, (ю) = aiS(го)e jюп‘ + Ei (to),   i = 1,..., N;

где S ( ю ) и E i ( ю ) являются DTFTs из s ( t )и e i ( t ), соответственно, a ω означает нормированную угловую частоту.

Учитывая пару сенсоров i и] при i Ф j , GCC между %_;(t) и X j (t) может быть записан как [15]:

π

R (т) ■ 2^ f X- (ю)X' (ю)^ j (ю)ejютdю,

-π где Xi (ю) - DTFT от %;(t); * - обозначение сопряженного оператора; Vij (ю) - подходящая весовая функция. Тогда TDOA от пары (ij) оценивается как

Т- =

τ ij

arg max _т R ij ^{( т )}

Fs        ’

где F s - частота дискретизации. Задача V j ( ю ) состоит в том, чтобы сделать R ij ( т ) точнее, чтобы оценка т ij стала более точной. Одним из наиболее распространенных вариантов является использование весовой функции фазового преобразования (РНАT); тогда

V » =

| X- ( ю ) X * ( ю )|

В массиве N сенсоров полный набор TDOAs рассчитывается как N(N - 1)/2. Если на них не влияет какая-либо погрешность измерения, то можно легко продемонстрировать, что только N - 1 из них являются независимыми, а остальные представляют собой их линейную комбинацию. Поэтому общепринятой практикой является использование эталонного сенсора в массиве и измерение N —1 TDOAs по отношению к нему. Назовем этот комплекс N —1 мер сокращенным набором TDOA. Без потери общности для приведенного набора TDОA можно предположить, что эталонный сенсор будет иметь индекс 1, а TDOAs Т1 j. в приведенном множестве, по соображениям компактности в обозначении, есть тj, j = 2,..., N.

Локализация звука на основе применения распределенных акустических сенсоров

Рассмотрим вопрос о локализации источника звука (определение местоположения злоумышленника на защищаемом объекте) путем объединения измерений, поступающих из разных узлов. Для идентификации DAS, от которого были получены измерения, мы будем использовать надстрочный знак m. С геометрической точки зрения, учитывая оценку TDOA т j ) , источник обязан лежать на ветви гиперболы (гиперболоида в 3D), фокусы которой находятся в m^{( m} ) и m j^m ) , а вершины c т j ) далеко друг от друга. Если источник и сенсоры являются копланарными, то местоположение источника может быть идеально получено путем пересечения двух или более гипербол [16], как показано на рисунке 3, и некоторые примитивные решения для локализации источника опираются на эту идею. Важно отметить, что, когда источник находится доста^точно далеко от узла, ветвь гиперболы можно спутать с его асимптотой։ в этом случае TDОA информативна только относительно направления, в котором находится источник, а не его расстояния от массива. В этом контексте удобнее работать с DOAs.

В общем случае пересекающиеся гиперболы представляют собой нелинейную задачу с очевидными негативными последствиями для вычислительных затрат и чувствительности к шуму при измерениях. В [17] предлагается реше ние для преодоления этой проблемы, которое опирается на проективное представление. Гипербола получена из TDOA т(jm) для сенсоров mim) и m(m), записывается как a j) х2 + bjm) xy + cjm) y2 + + djm) x + ejm) y + f(m) = 0, где коэффициенты

^{( m} ) г,^{( m} ) ,„^{( m} )     ^{( m} ) ,,^{( m} ) f^{( m} )

aij , ij , cij , ij , eij , fij определяются в замкнутом виде с помощью mi(m), m(m) и т(jm). Приведенное уравнение представляет собой ограничение, накладываемое на местоположение источника. При наличии

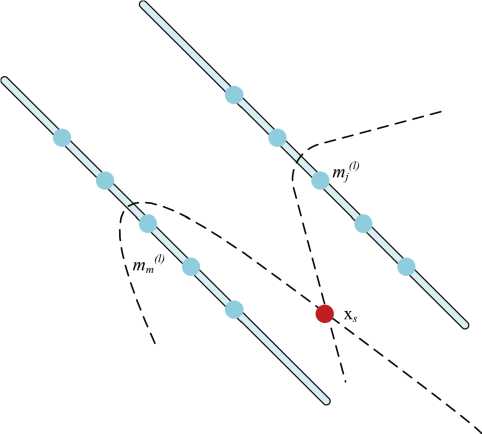
Рисунок 3. Определение местоположения источника звука на пересечении гипербол, полученных из TDOAs

шума в системе ограничение не соблюдается, и остаток может быть определен как

£ jm) (x) = V (j”) (a jm) x2 + bm) xy +

+ cj) y2 + dj) x + ej) y + fj m)), где Vjm) = 1 для всех TDOAs которые были признаны надежными, и 0 в противном случае. Остальное укладываются в вектор e(x), а источник локализуется путем минимизации функции затрат JHDOOA)(x) = e(x)T e(x).

Если на измерения TDOA влияет только аддитивный белый гауссовский шум, то J HDOOA ) (x) пропорционально функции затрат ML . Упрощение оценочной функции локализации может быть достигнуто, если будет принят эталонный сенсор, за счет узлов, совместно использующих общие часы. Можно предположить, что эталонным является первый сенсор в первом датчике (то есть i = 1 и m = 1), и мы также устанавливаем m ।¹) = 0;

то есть начало отсчета системы совпадает с эталонным сенсором.

Более того, можно отбросить индекс массива m при присвоении глобального индекса сенсорам в различных датчиках, начиная от j = 1 до j = NM . Можно также линеаризовать функцию стоимости локализации, переставляя члены в формуле для вычисления т j ) и полагая, что i = 1, после чего легко вывести

IIx .11—М lxs - тА |, где Гj = cтj. В [18] было предложено представить проблему локализации источника в системе отсчета пространственного диапазона։ точка x = [x,y]T в пространстве отображается на

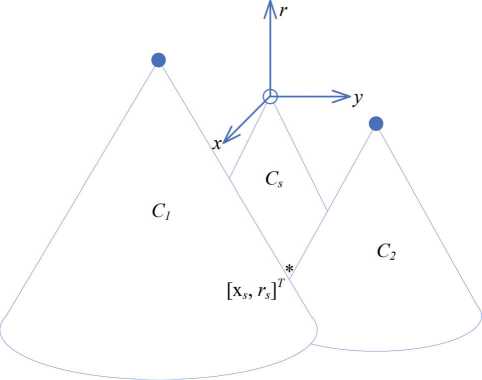
Рисунок 4. Определение источника звука в пространственно-временной системе отсчета

, при-

TT xs , ^r s I

трех мерный пространственный диапазон, как | x ^T r ] ^T .где , = ||x . - x|| — ||xj|.

При отсутствии шума и ошибок измерения г является разницей диапазона относительно источника x _s между опорным сенсором и сенсором внутри x. Если заменить r _s = -||x _s ||, то можно интерпретировать ||x _s ||- Г"j = ||x _s - m J| как уравнение отрицательного полуконуса C _j в пространственно-временной системе отсчета, вершина которого находится в ^ т'¹ , , Г j чем с апертурой п/4, а исходная точка лежит на ней. Уравнение ||xJ |- Г"j = ||x _s - тД может быть повторено для j = 2,..., N х M , и источник обязательно будет лежать на поверхности всех конусов. Кроме того, диапазон r _s источника от эталонного сенсора должен соответствовать ограничению r _s = -||xJ|, которое представляет собой уравнение конуса C S , вершина которого находится в ^ m 1 ^T , 0^ | с апертурой п/ 4. Таким образом, оценка источника ML представляет собой точку на поверхности конуса в , = -||xJ|, ближайшую ко всем конусам, определенным II x s |I — r^;j = ||x _s - m j .||, какпоказано нарисунке 4.

Возведя в квадрат обе части уравнения II x s |I- r^; j = ||x _s - тД и учитывая, что x S + y S -- r S = 0, получим уравнение плоскости в системе отсчета пространственного диапазона, на которой должен лежать источник:

12      2     2

xjxs + y,ys - .Vs - 2 (x,+ yj-r,) = 0.

Отметим, что данное уравнение не выполняется точно при погрешности в оценке разности диапазоноврасстояний /•j , поэтомуостаток

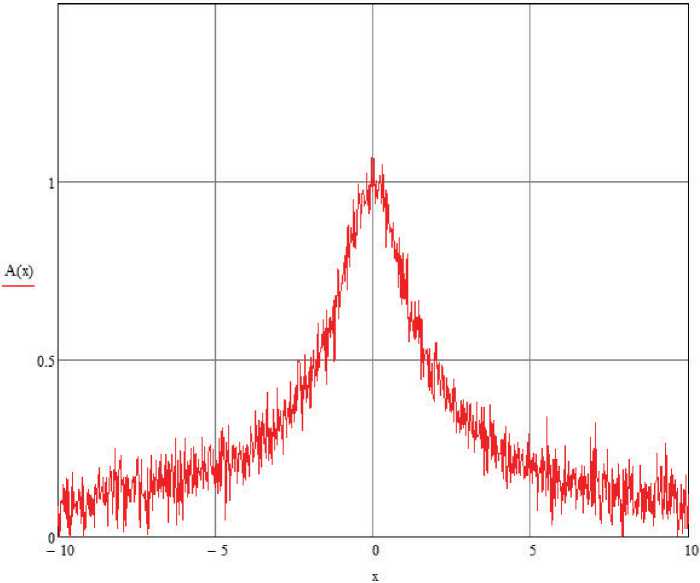
Рисунок 5. Зависимость амплитуды сигнала обратного рассеяния от кратчайшего расстояния между источником звука и оптическим волокном

ej = xjxS + yjyS - rjrS - 2(xj+ yj- - ).

На основе определения e _j сферическая функция стоимости LЅ определяется формулой [19]

NM

JT )(x,, rs) = Z ej.

j = 2

Большинство методов оценки LS используют данную функцию затрат и отличаются только дополнительными ограничениями. В свою очередь, неограниченная оценка наименьших квадратов (ULЅ) [20–24] локализует источник звука, поскольку x s^ULS ) = arg min J SP^T_P^DOA ) (x s , r s ).

^x s . r s

Уточним, что отсутствие какого-либо ограничения, которое связывает x s и r s , обеспечивает во многих приложениях плохую точность локализации источника звука. Поэтому метод наименьших квадратов вносит это ограничение как

^Г) = argmin J^O)(xs,rs);

^x s , r s

subject to rS =-||xs||.

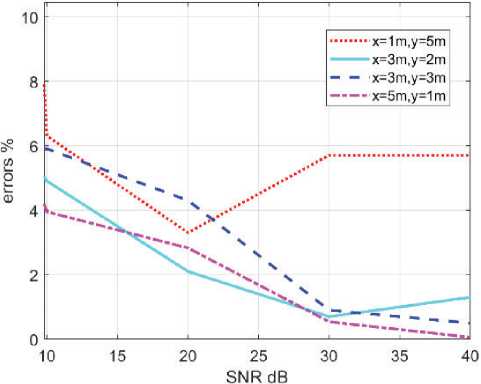
На основе полученного уравнения сферического пересечения [25], метода наименьших квадратов с линейной коррекцией [26] и метода наименьших квадратов разности квадратов разности диапазонов [27] были предложены оценки, которые различаются для процедуры минимизации, начиная от итерационных решений до решений в замкнутой форме. Отметим, что все эти методы предполагают наличие глобального контрольного сенсора и синхронизацию, действительную для всех узлов. Альтернативные решения, позволяющие преодолеть это технологическое ограничение, были предложены в [28; 29]. Здесь в преимущество была поставлена концепция распространения конуса в пространственно-дальней привязке. В частности, в [29] определен конус распространения, немного отличающийся от конуса, определенного в ||xs||-r^j = ||xs -mj.||: вершина находится в источнике и rs = 0. Как следствие, при отсутствии ошибок синхронизации все точки ^x

Пример расчета для помещения с двумя оптическими волокнами

В качестве примера реализации алгоритмов на основе рассмотренных выше моделей было выполнено моделирование акустического воздействия на оптические волокна и произведены расчеты погрешностей определения коорди-

Рисунок 6. К определению местоположения источника звука в помещении с двумя волокнами нат источника звука в помещении с размерами 6 × 6 м2 и двумя оптическими волокнами, расположенными параллельно вдоль противоположных стен. Координату х источника акустического сигнала вдоль оси волокна определяли в точке максимума амплитуды сигнала, регистрируемого распределенным акустическим датчиком в соответствии с рисунком 5.

Координату у источника акустического сигнала вдоль оси, перпендикулярной оптическим волокнам, определяли из соотношения амплитуд сигналов, принимаемых оптическими волокнами в точках с координатой х. То есть из соотношений максимальных значений сигналов, принимаемых параллельными волокнами (см. рисунок 6). Результаты вычислений погрешностей определения координат источника звука в зависимости от уровня шума в помещении для ряда значений координат источника звука представлены на рисунке 7. Как показывают результаты моделирования, при отношениях «сигнал/помеха» более 10 дБ погрешности не превышают 10 %. Согласно полученным в результате моделирования данным, можно сделать вывод, что источник звука расположен под камерой наблюдения.

Заключение

В статье рассмотрены модели для определения координат источника акустического сигнала с помощью распределенных оптоволоконных сенсоров. В качестве примера представлены ре-

Рисунок 7. Погрешности определения координат источника звука в зависимости от S^R для ряда значений координат источника звука зультаты моделирования для условий помещения с двумя параллельно проложенными вдоль противоположных стен кабелями с оптическими волокнами. Приведены оценки погрешностей определения координат источника звука в зависимости от уровня шума. Оценки получены для ряда значений координат источника звука. По результатам вычислений при отношении «сиг^нал/ шум» более 10 дБ относительная погрешность не превышает 10 %.