Поток энергии вихревого поля в фокусе секансной градиентной линзы

Интерес к острой фокусировке лазерного излучения в последнее время не ослабевает [1– 4]. С помощью линз с высокой числовой апертурой можно формировать как фокусные пятна с увеличенной глубиной [1, 5–7], так и увеличенное по глубине затенение на оптической оси длиной до 48 λ [8], осуществлять фокусировку света в широком диапазоне длин волн [4]. Оптические системы с высокой числовой апертурой часто используются в микроскопии [9, 10]. Одно из перспективных направлений использования острой фокусировки и локализации света с максимальной интенсивностью в свободном пространстве – оптический захват микрообъектов [11]. Силу, действующую со стороны света, можно представить в виде суммы градиентной и рассеивающей сил [12]. Градиентная сила при прозрачной частице направлена в сторону максимума интенсивности, в то время как рассеивающая сила направлена к пучку света. В [12, 13] показано, что рассеивающая компонента силы на рэлеевскую частицу действует по направлению вектора Пойнтинга. Однако можно создать такое распределение поля в начальной плоскости, что в фокусной плоскости проекция вектора Пойнтинга на ось распространения света будет отрицательна [14]. Это означает, что в такой области рассеивающая компонента силы, действующей со стороны света на рэлеевскую частицу, также будет отрицательна. В работах [15] предлагалась такая фокусировка света, с помощью которой можно сформировать требуемую область с обратным потоком энергии, однако при этом область с обратным потоком энергии располагалась в области с локальным минимумом интенсивности. В области, где интенсивность света максимальна, поток направлен в положительном направлении оптической оси.

18287/2412-6179-CO-688.

В предыдущей работе [16] была продемонстрирована возможность значительного увеличения интенсивности обратного потока энергии ( Sz <0) в фокусе за счёт использования градиентной линзы Микаэляна. Кроме того, там рассматривалось выведение его из материала линзы за счёт цилиндрического выреза и локализация области с максимальной интенсивностью и положительным потоком Sz внутри материала линзы, чтобы он не мешал захвату рэлеевских частиц. Однако использование такого выреза накладывает ограничение на размер и местоположение объекта, который может в нём находиться. В некоторых случаях удобнее, когда обратный поток находится за плоскостью линзы. В данной работе рассматривается оптимизация параметров линзы Микаэляна, при которых область с обратным потоком энергии находится за выходной плоскостью линзы. Выбор именно градиентной линзы Микаэляна обусловлен наилучшим качеством (интенсивность и ширина фокусного пятна) фокусировки излучения [17]. Кроме того, в данной работе показано, что область с обратным потоком энергии (область с отрицательными значениями проекции вектора Пойнтинга на оптическую ось) может располагаться в области с максимальной интенсивностью, то есть нет необходимости как-то отгораживать область с положительным потоком, как в [16]. Такой эффект можно использовать для оптического захвата рэлеевских частиц.

Фазовый вихрь 2-го порядка

Для расчётов бралась градиентная линза Микаэляна, рассчитанная для фокусировки излучения на своём торце.

Показатель преломления такой линзы изменяется в соответствии с формулой [14]:

147 нм, эти значения были выбраны в ходе оптимизации для максимизации интенсивности в фокусной

n ( r ) = n 0

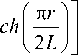
где n 0 – показатель преломления линзы на оси, r – радиальная координата, L – длина линзы. При этом диаметр линзы был равен D = 11,7 мкм, длина линзы L = 4,89 мкм, длина волны X = 1,55 мкм. Показатель преломления на оси линзы n (0) = 3,47 (кремний), на краю линзы n ( D /2) = 1,0. На одну из поверхностей такой линзы нормально падал плоский пучок света, имеющий левую круговую поляризацию и фазовый вихрь порядка m = 2 (рис. 1).

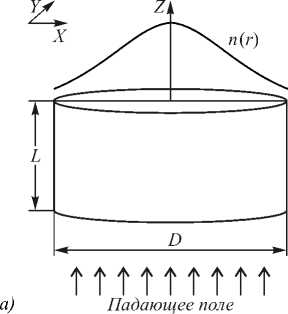
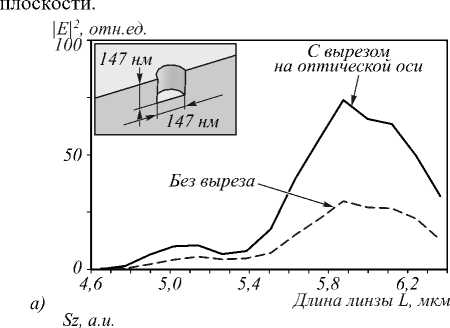
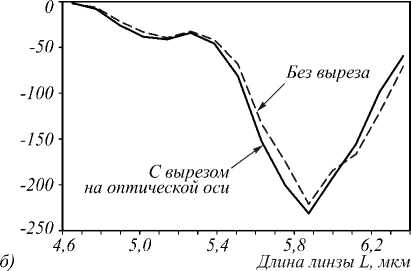
Рис. 2. Интенсивность (а) и схема цилиндрического выреза в выходной плоскости линзы (вставка в разрезе) и проекция вектора Пойнтинга (б) на ось Z

• б)

Рис. 1. Рассматриваемая градиентная линза (а) и фаза падающего поля (б), имеющего левую круговую поляризацию

При моделировании методом FDTD шаг разбиения составлял X /70 по всем трём осям координат. Линза представляет собой цилиндр, падающее поле – плоское с единичной амплитудой. Для формирования обратного потока в фокусе линзы падающее поле содержало фазовый вихрь порядка m =2, использовалась левая круговая поляризация, поле было ограничено апертурой, равной диаметру линзы. Такая линза фокусирует плоскую волну на своей границе. Однако интерес представляет распространение поля с обратным потоком интенсивности дальше за границей линзы. Регистрация поля осуществлялась на оптической оси на расстоянии 50 нм от поверхности линзы. На рис. 2 представлен результат такого моделирования в зависимости от длины линзы L . Моделировалось прохождение света через линзу с вырезом на оптической оси, аналогичной работе [16], и без такового. Вырез был цилиндрический, диаметром 147 нм и длиной

Из рис. 2 видно, что для максимизации интенсивности и потока энергии на оптической оси предпочтительнее градиентная линза Микаэляна с высотой, больше расчётной, что согласуется с результатами [16]. Ширина интенсивности на выходе по полуспаду FWHM = 539 нм = 0,348 X , а ширина потока Sz по полуспаду FWHM=193 нм = 0,124 X . Так, для данных условий максимальная интенсивность света на границе линзы, равно как и максимальное по модулю негативное значение потока интенсивности Sz , наблюдается при длине линзы L = 5,88 мкм. Также из рис. 2 видно, что наличие выреза усиливает как интенсивность электрического поля на оптической оси, так и модуль потока вектора Пойнтинга (менее выражено).

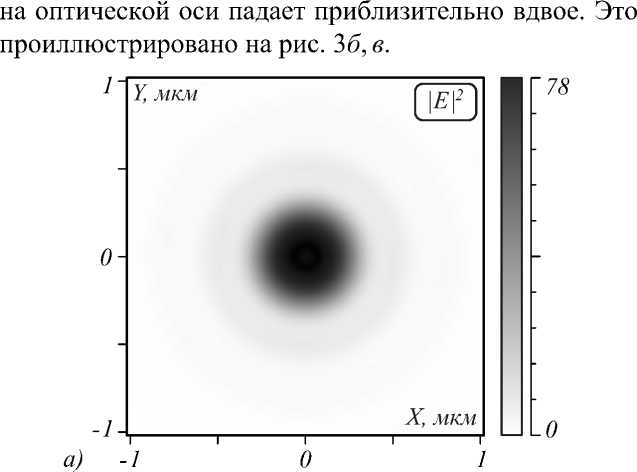
Но интересно, что при данной высоте линзы на её границе на оптической оси образуется область, где обратный поток интенсивности ( Sz < 0) сочетается с почти максимальной интенсивностью электрического поля (рис. 3). В отличие от данного случая в предыдущих работах обратный поток вектора Пойнтинга возникал в области, где интенсивность света не максимальна, а в точках максимальной интенсивности поток вектора Пойнтинга был направлен в положительном направлении вдоль оси Z . В рассматриваемом случае поток энергии в обратном направлении в 4,86 раза больше по модулю, чем в прямом направлении оси Z .

Если убрать вырез, то проекция вектора Пойнтин-га на ось Z становится примерно на 4,5 % меньше по модулю, но сильно не меняется, а вот интенсивность

\EV, отн.ед.

Sz, отн.ед.

б)

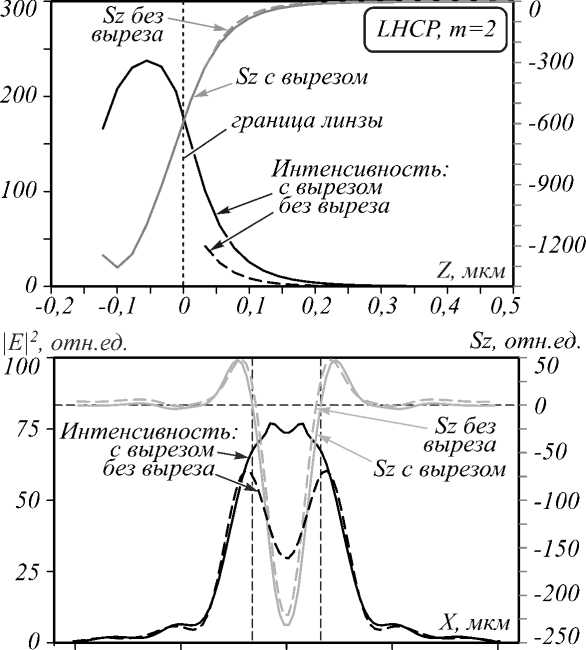
Рис. 3. Интенсивность |E|2 (а) и проекция вектора

Пойнтинга Sz за линзой длиной L=5,8 мкм при наличии и отсутствии в ней цилиндрического выреза: их сечения вдоль оси Z (б) и вдоль оси X (в) на расстоянии 50 нм за линзой

в)

Цилиндрический векторный пучок 2-го порядка

На рис. 4 представлено падающее поле, имеющее поляризационный вихрь 2-го порядка. В качестве освещающего пучка использовался цилиндрический векторный пучок второго порядка, вектор Джонса для него равен

- sin ( 2ф)

cos ( 2 ф )

где ф - азимутальный угол в цилиндрической системе координат, выбранной таким образом, что ось Z совпадает с направлением распространения пучка.

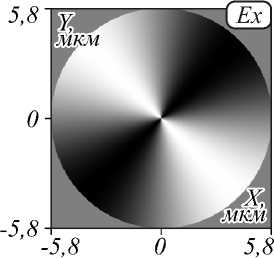
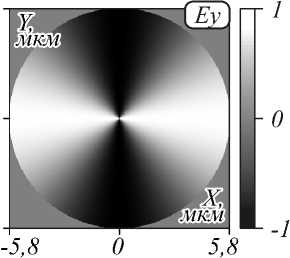
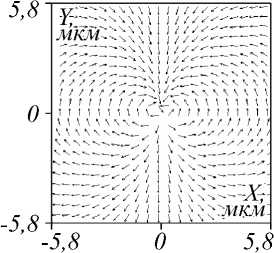
Рис. 4. Падающее поле, имеющее фазовый вихрь второго порядка

Такое падающее поле тоже генерирует в остром фокусе область на оптической оси, в которой проекция вектора Пойтинга на ось Z отрицательна. Зависимость интенсивности и проекции Sz сразу за линзой в зависимости от её длины выглядит для данного падающего поля похожим образом, как и на рис. 1 в предыдущем случае (рис. 5). Наибольшие интенсивность и поток в данной точке по-прежнему получаются при высоте линзы L = 5,88 мкм.

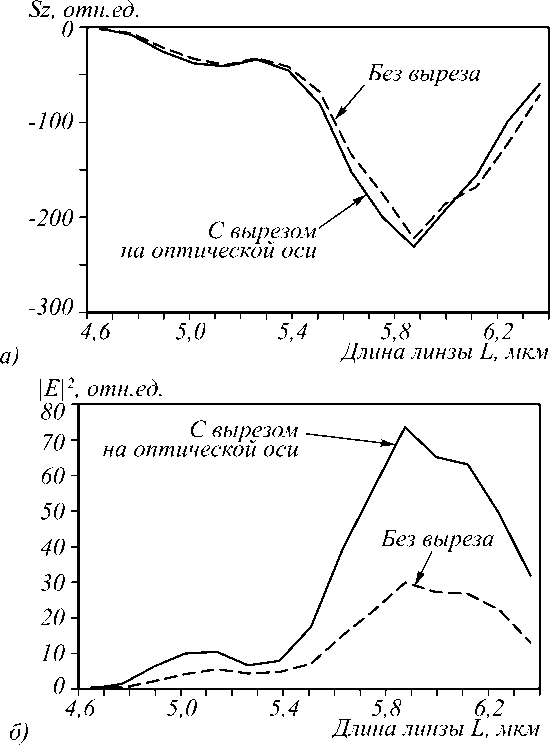
Рис. 5. Интенсивность в выходной плоскости (а) и проекция вектора Пойнтинга (б) на ось Z для падающего цилиндрического векторного пучка второго порядка

Из рис. 5 видно, что в случае цилиндрического векторного пучка зависимости схожие, и с вырезом по-прежнему интенсивность выше примерно вдвое.

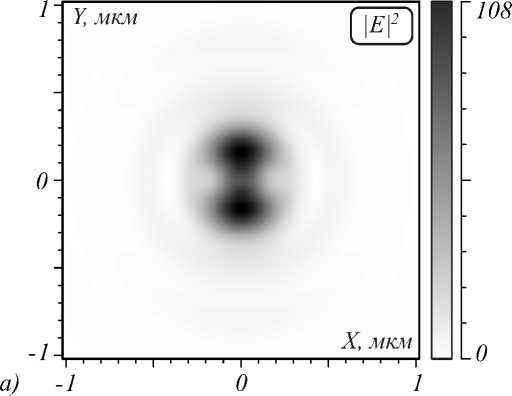
Однако в случае фазового вихря интенсивность меньше на 28% по сравнению со случаем падающего цилиндрического векторного пучка, который показан на рис. 6. Отчасти это объясняется тем, что в случае цилиндрического векторного пучка в фокусной плоскости образуются два пятна, которые по площади меньше кольца.

б)

в)        -1

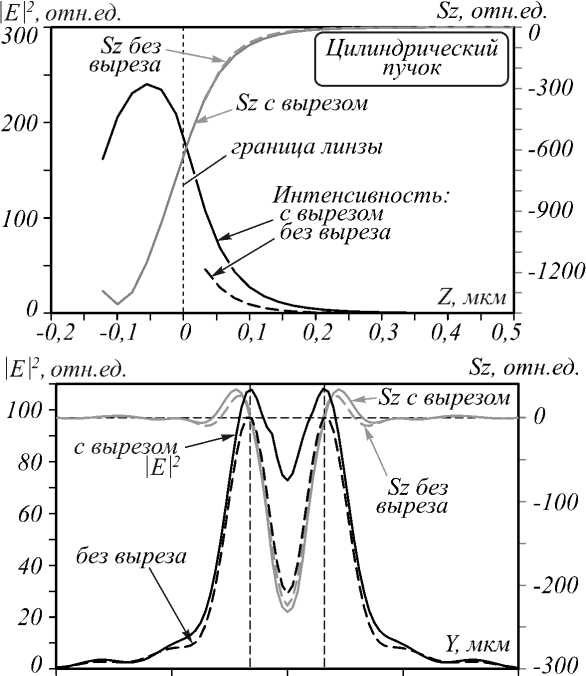
Рис. 6. Интенсивность |E|2 (а) и проекция вектора

Пойнтинга Sz за линзой длиной L=5,88 мкм при наличии и отсутствии в ней выреза: их сечения вдоль оси Z (б) и вдоль оси Y (в) на расстоянии 50 нм за линзой

При этом максимальные значения проекции вектора Пойтинга вдоль оси Z по модулю больше примерно на 4%, чем в случае фазового вихря второго порядка (рис. 6 в ).

Заключение

В работе показано, что с помощью цилиндрической линзы Микаэляна с вырезом на оптической оси, доходящим до выходной плоскости, можно сфокусировать пучок с фазовым вихрем второго порядка или поляризационным вихрем второго порядка, причём на выходной границе линзы образуется область с об- ратным потоком энергии. Оптимизируя размер выреза и длину линзы, можно добиться максимальной интенсивности света и обратного потока вектора Пойн-тинга, причём область с обратным потоком совпадет с областью максимума интенсивности. Такой эффект можно использовать для захвата силой со стороны света рэлеевских частиц.

Работа выполнена при поддержке Российского научного фонда в частях «Фазовый вихрь второго порядка» и «Цилиндрический векторный пучок второго порядка» (грант 18-19-00595), а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части «Введение» и «Заключение».