Потоки в квазиклеточных сетях

В работах автора [1, 2, 3] рассмотрены вопросы проектирования и применения квазиклеточных сетей (рис. 1). Квазиклеточные сети представляют собой особый тип дискретных структур, не имеющих сигнатуру. Квазиклеточные сети позволяют моделировать динамические системы на различных уровнях. Следует отметить, что микро- и макромоделирование в квазиклеточных сетях реализуется в рамках одной фундаментальной дискретной структуры [1].

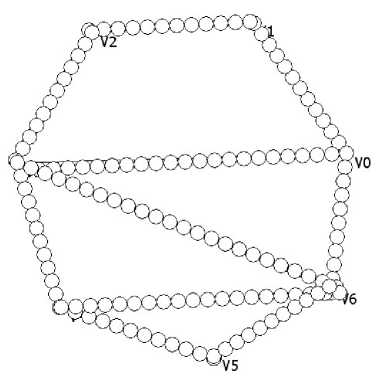
Рис. 1. Квазиклеточная сеть.

Статический аспект квазиклеточных сетей описан в работах, посвящённых синтезу структуры. Немаловажным вопросом при рассмотрении динамических аспектов является оценка циркуляции и функционирования квазиклеточных сетей и нахождение значений соответствующих величин. Для последующего рассмотрения и оценки квазиклеточных сетей следует установить понятие потока в квазиклеточной сети. В различных предметных интерпретациях [3] поток представляет собой совокупность движущихся объектов, находящихся во взаимодействии. При этом движение потока можно описать через поведение его отдельных элементов [4, 5]. Среди примеров потока можно рассматривать движение жидкостей или газов в трубопроводах, водопроводных, канализационных сетях, движение транспортных средств на автомобильных дорогах, движение пассажиров в транспортных системах, товарно-денежные отношения и др. Во всех приведённых ситуациях предполагается наличие некоторой единицы потока. В случае транспортных потоков такой единицей является транспортное средство, в потоках жидкостей или газов единицей является молекула и т. д. [5, 6, 7 и др.] Кроме того, поток рассматривается как единый объект, тем не менее, состоящий из более мелких объектов, которые рассматриваются как сами по себе, так и во взаимодействии. Таким образом, поток полностью отвечает принципам системного подхода и концепции сложных систем, в частности обладает свойствами целостности и членимости. Многие явления, характерные для потоков в целом, часто сводят к рассмотрению поведения отдельных объектов, из которых состоит поток. Например, давление газа в сосуде объясняется ударами отдельных частиц этого газа об стенки сосуда [7].

Особое внимание следует уделить вопросам моделирования потоков. Согласно принципам декомпозиции, на микро-уровне моделирование потока сводится к моделированию отдельных объектов, из которых состоит поток [4, 5]. Также стоит отметить, что в ряде работ [6, 8 и др.] поток рассматривается как объект. На макро-уровне моделирование потоков в сетях рассматривается как элемент теории графов. Поток рассматривается как некоторая величина, определяемая для ребра или вершины графа [3, 9]. Учитывая очевидные сходства квазиклеточных сетей с приведёнными подходами к моделированию потоков в сетях, а также связь квазиклеточных сетей с другими дискретными структурами на этапе синтеза, особое внимание следует уделить вопросам моделирования и оценки потоков в квазиклеточных сетях.

Учитывая, что квазиклеточная сеть состоит из элементов вида:

Q i = ( B,, C„ S i ) ,                                                  (1)

где Bi — неизменные (базовые) параметры клетки (от англ. basic), Ci — параметры клетки, изменяющиеся при прохождении фишек через клетку (от англ. changeable), Si — параметры фишки как микрообъекта, находящегося в клетке, т. е. переменные состояния (фазовые переменные) клетки (от англ. state); следует в качестве потока в квазиклеточной сети рассматривать множество векторов (C1, C2, …, S1, S2, …) значений Ci и Si, циркулирующих в квазиклеточной сети. В работах [3, 8, 9, 10] отмечается, что поток является как характеристикой отдельных элементов графа, так и характеристикой сети в целом. Выше рассмотрены вопросы измерений параметров циркуляции в квазиклеточных сетях. Измерения величин проводятся на некотором участке квазиклеточной сети:

Q ^{( m )} c Q

■ Q , e Q ( " '                                                          (2)

Q , = ( B , , C , , S , )

Рассматривая квазиклеточную сеть, синтезируемую методом базового графа G = (V, U) , для каждой клетки Q i = ( B i , C i , S i ) можно однозначно установить базовое ребро:

Q _i ∈ U _k ,                                                   (3)

тогда поток на каждом ребре U k можно свести к измерению параметров циркуляции во всех клетках, для которых указанное ребро является базовым. Рассмотрим множество клеток на ребре:

Q ⁾ = ( Q i ^{( k )} , q2‘ ⁾ , Q ⁾ ,... )

Q ) = ( x j* ) , _h ) , c jk ) ,_s i* ) ,... )

^

Q ik ) e U k

, ( x ‘ ‘ ) - x ( - 1 ) 2 + ( y ( * ) - УЙ) ² 2 4 R 2

С течением модельного времени для клетки Q i^(k) меняются значения компонент векторов C i^(k) = (C i1^(k) , C i2^(k) , …) и S i^(k) = (S i1^(k) , S i2^(k) , …) , т. е. фактически речь идёт о функциях C ij^(k) (t m ) и S ij^(k) (t m ) , задаваемых численно и определяемых при циркуляции в квазиклеточной сети. Тогда величина потока определяется исходя из указанных функций способами, рассмотренными ранее при работе с измерительными участками квазиклеточных сетей. Тогда за время моделирования T m через клетку проходит поток, величина которого:

T _m

^ ^{( C j )} (T . ) = I C ijk ⁾ (<,, )                                                  (5)

t _m =0

T

f ^{( $ 1 )} (T . ) = I S C ¹ ( t . )                                             (6)

t _m =0

Стоит отметить, что соотношения (5-6) имеют вид дискретных сумм, поскольку время в квазиклеточных сетях дискретно. Однако при рассмотрении непрерывного времени,

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 9 № 3 (20), 2013, ст. 4

указанные соотношения приняли бы вид определённых интегралов по времени.

Для оценки потока на ребре U k следует просуммировать потоки по всем клеткам, для которых требуемое ребро является базовым, т. е. при выполнении условия (4) потоки на ребре за время вычисляются по формулам:

T _m

$-'(T.) = Z #(c-i(t.) = Z ZCX)

QA              Qi ^Uk tm =0

T

^(T ) = Z ?('j(T. ) = ZZ Sj'(t- )

Q . e U k                   Q . ^ U k t m = 0

Предложенные оценки величин потоков основаны на рассмотренных ранее измерений параметров в квазиклеточных сетях. Однако ранее рассмотрены оценки для произвольных участков квазиклеточных сетей, а предложенные соотношения (5-8) позволяют оценить потоки для отдельных рёбер. Рассмотренные соотношения позволяют моделировать потоки в сетях на микро- и макро-уровне, в отличие от теоретико-графовых моделей, описанных в работах [3, 9], предполагающих потоки как макропараметры рёбер графа. Однако ранее рассматривалась идея преобразования графа в квазиклеточную сеть. Указанное преобразование позволяет решить проблему моделирования динамики и перехода от макро- уровня в теории потоков в сетях к микро-уровню.

Также следует отметить, что при измерении в квазиклеточных сетях также рассматривались средние величины:

M - I T ) " =

T _m

Z - (' )  ZZ Cj1 (tm )

Q i ^ U k

T m

_ ^Q i ^eU k t m = 0

T m

T m

M I" - US ' ) T, ) " =

z - ⁽ S ij ) ( T m ) zz s k ) ( t m )

^Q i ^eU k _ ^Q i ^eU k t m = 0

TT mm

Следует отметить, что соотношения (9-10) используются для оценки математического ожидания при проведении компьютерного модельного эксперимента и получении случайных величин на ЭВМ [11]. Тогда величины дисперсии:

D [f(Cj

= M [ ( f ^{( C}- > ) ²

- M² ( f ( C - ¹ ) 2

D [fI ^j

= M [ ( f ^{( s} S ^- ' ) 2

-

M ²

( fC ’ , ) ) ²

T                             Tm

Z]: ( C j ⁾ ( t m ) ) ²    ZZ C j ⁾ ( t m )

Q . eU k t m = 0 V ^Q i ^{G U} k t m = 0 J

TT mm

T                            Tm

Z Z ( S j ⁾ ( t m ) ) ² Z Z S j ) ( t m )

Q i ^{e lJ}k t m = 0 V ^Q - ^{e U} k t m = 0 J

TT mm

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 9 № 3 (20), 2013, ст. 4

Таким образом, измерения в квазиклеточных сетях позволяют оценить динамические характеристики потоков в сетях. Следует отметить, что рассмотренные оценки относятся к квазиклеточным сетям, синтезированным методом базового графа, и позволяют вычислить величины потоков на рёбрах базового графа.

Для квазиклеточных сетей, синтезированных другими методами, используются оценки, рассмотренные выше в работах автора [1, 2 и др.]. В общем случае измерения параметров в квазиклеточной сети производятся на участке Q^ :

lQ(" с( Q

■ Q г Q" (13) Q = ( в , C , S )

В частном случае:

Q ^{( m )} A Q = Q = Q m (14) рассмотренные измеряемые величины позволяют оценить поток через сеть. Тогда потоки через квазиклеточную сеть за время Т _т вычисляются по формулам:

T _m

-'    (T m ) = X j    (Т , ) = ZZ C j ⁾ (' . )                            (15)

Q i                      Q i t m =0

T _m

5QS''kT. ) = Z 5  и ) = ZZ sj ⁾ ('. )                            ⁽¹⁶⁾

Q i                      Q i t m =0

Нетрудно видеть, что соотношения (15-16) отличаются соответственно от (9-10) тем, что суммирование производится по всей квазиклеточной сети, а не по клеткам с одинаковым базовым ребром Uk. Тогда оценки математического ожидания и дисперсии величин потоков для всей квазиклеточной сети примут вид:

D rfi

D r ^ QS •'

M -   । T ) ' =

M -S'' (T.)_

=M [ ( f ^j ) 2

=M [ (4 S - ¹ ) ²

- M1

-M ²

T _m

X5(C"' (T)  XX Cj1 (tm)

Q . _ Q . t m = 0

TT mm

X^’("S'' (T. )

Q i

T m

T

m

XX Sj' (tm )

Q i t m = 0

T m

\ ( C j ) ξ _Q

( S i ) ξ _Q

T                           Tm

Z]L ( C j ⁾ ( t m ) ) ²    XZ C j ' ( t m )

Qi tm =0_______________ V Qi tm =0

TT mm

T                            ^T m               ²

ZZ (Sj) (tm) )2   ZZ Sj) (tm)

Q i t m = 0 V ^Q i t m = ⁰

T                T ²

mm

Важной особенностью алгоритмов теории потоков в сетях, рассмотренных в работах [3, 9] является наличие в сети стока и истока, а также тот факт, что сеть является взвешенным и ориентированным графом. Фактически, рассматриваемые в этих работах графы преобразуются в квазиклеточные сети с микро-циркуляцией [2]. Несмотря на это, рассмотренные выше оценки потоков не зависят от классификации квазиклеточных сетей по типу циркуляции и позволяют оценивать потоки в квазиклеточных сетях на основе компьютерного моделирования.

Таким образом, квазиклеточные сети обеспечивают моделирование потоков при различных предметных интерпретациях. Следует также отметить возможности моделирования потоков на микро- и макро-уровне в рамках одной дискретной структуры. Приведённые выше зависимости предназначены для реализации компьютерного моделирования потоков и оценки результатов работы компьютерных моделей.