Поведение скорости в однородном изотропном турбулентном потоке на начальном этапе

Неустойчивые движения вязкой жидкости, широко распространенные в природе (движения воздуха. в атмосфере, течения воды в океанах, морях, реках, каналах) и технических устройствах (течения в водопроводных трубах, в газопроводах, турбинах, насосах и компрессорах, в соплах ракетных и реактивных двигателей), при которых малые вначале возмущения растут, существенно изменяя характер начального движения, приводя его к хаотическим изменениям по времени и координатам, при которых могут быть выделены статистически точные их осредненные значения [1], называют турбулентными. Имеет место представление о непрерывном потоке энергии из крупномасштабных турбулентных областей в мелкомасштабные, где вязкие напряжения приводят к диссипации кинетической энергии этих движений в тепло. Без наличия внешних источников энергии турбулентные движения вырождаются. Действие вязкости кроме того приводит к тому, что турбулентность становится более однородной и менее зависит от направления.

Одним из первых экспериментов было измерение вырождения кинетической энергии турбулентности [2]. Оказалось, что на некотором промежутке расстояний x от решетки энергия рассеивается как и-2 ~ (X - Xо), (1) и — среднеквадратичное значение компоненты пульсационной составляющей скорости (параллельной среднему течению), x0 — постоянная. Начальным периодом вырождения назван период времени, для которого справедлив закон вырождения (1), т. е. кинетическая энергия (в единице объема, жидкости) обратно пропорциональна, времени, отсчитываемому от (условного) момента, в котором энергия была, бы бесконечно большой.

На больших расстояниях рассеяние энергии становится более быстрым, чем это следует из формулы (1).

Полученные при ряде предположений зависимости для начального периода, вырождения скорости приводили в своих работах Хинце [1], Седов [3].

В настоящей работе принимается модель потока. как смеси двух режимов [4, 5]: турбулентного ( т ), взятого с весом, равным значению коэффициента перемежаемости y = ^Рт, и вяэкого ( v ), взятого с весом (1 — y )• При этом для одноточечной P 1 и двухточечной P 2 плотностей вероятностей принимается:

Pi = y (P1) т + (1 — Y) (P1) v и P2 = Y (P2)т + (1 — Y)(P2)V •

Тогда.

u 2 = Yu T ^{+ (1 —} Y ) u V • (2)

При изучении динамики изотропной турбулентности используется уравнение Кармана-Ховарта. [1,2,6], связывающее величины продольных корреляционных моментов второго B ll = и ² f (f ( r, t ) — продольный коэффициент корреляции второго порядка) и третьего порядков B ll,l = = и ³ k, (к ( r, t ) — продольный коэффициент корреляции третьего порядка), в качестве исходного соотношения:

dBLL _ X д ( 4 (R dBLL А dt r4 dr v ( LL,L + v dr )) ’ ° здесь v — коэффициент динамической вязкости, r — расстояние между точками.

Следует отметить, что уравнение (3) незамкнуто, поскольку представляет собой одно соотношение, связывающее две неизвестные функции.

В случае однородной изотропной турбулентности непосредственно из уравнения (3), умножая его на. r ⁴ и иитегршруя по r от () до го . получается

*Работа выполнена при финансовой поддержке АВЦП «Развитие научного потенциала высшей школы» (проект 2.1.1/11133) и ФЦП «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы».

соотношение [1,2,6]:

∞ и 2 (t) У r 4 f (r,t) dr 1 - (u 3 (t) r 4k(r,t))|0° =

∞

= 2 vu ²( t )

(r ⁴ d^v-

шений: перехода к одноточечному описанию (ЛЛ = = го ), инерционного интервала и предельного перехода при ЛЛ ^ 0, где оно совпадает с выражением по Ю.М. Лыткину, Г.Г. Черных [8,10]:

Принято считать, что все корреляции скорости при однородной турбулентности на больших расстояниях между двумя точками убывают по экспоненциальному закону, т. е. f стремится к нулю при r , го быстрею. чем r5. i1 lim (r4 f ) = 0. Что r→∞   ∂r же касается r4k(r, t), то его полагают тоже обычно

2 к + = D^LLT T

^Т     v 3 a 1

здесь D LL = 2 и Т (1 — f_T ) = C ( er )² / ³ — продольная структурная функция, f_T ( r,t ) — продольный

коэффициент корреляции второго порядка, e —

т 1 скорость диссипации, тT = —

1      ψ 1²

Λ^{2 +} r ²

стремящимся к нулю, когда r неограниченно возрастает. Отсюда. Лойцянским [7] был получен вы-∞ вод о том, что величина и2(t) J r4f (r, t) dr = Loi = 0

= const. Обычно этот интеграл называют инвариантом Лойцянского. Принимается [1], что (Loi) _Т ~ иТ Л5 11 (Loi) _V ~ и V А 5. где Л — продольный интегральный корреляционный масштаб (чисто турбулентный режим), А — тейлоровский микромасштаб (вязкий режим).

Ради справедливости следует учесть замечание Хинце [1] со ссылкой па. работы Бэтчелора, и Пра-удмепа, что в однородном пеизотроппом потоке lim r ⁴k( r, t ) = 0. т. с. в общем случае Loi = r→∞

= Loi( t ) и не является инвариантом.

В рамках модели, использующейся в настоящей работе, принято гипотетическое соотношение Loi( t ) = y (Loi) т + (1 - Y ) (Loi) v -

— время релаксации при двухточечном описании,

D ll = D LL + 2 D NN. N — нормаль к r. C. a. a 1. ф 1 — постоянные. В работе [6] на основе многих

экспериментальных данных предложено значение C = 1 - 9.

Запись уравнения (4) с учетом (6) в виде

d (и Т / т ( € 1)) _ 1

dt = € 4

^{1 д} 3 ^{d ( и} Т ^f T ^{( €} 1⁾⁾

Л2 д€ 1 ^{€ 12 Кт} —%— /

™ ^€ i = ЛЛ ” 1»¹ B = 2 • C^ ■ u00o л»■" Bd^€ i = = V—f T fT.

Решение последнего уравнения при граничных условиях ^f T ^ 1=0 = 1. f r ^ 1= ^ = ⁰ имеет вид [8]:

B^€ 1 = ^{— 2} Р 1 ^— f r ⁺

^{+ ln} ( 1 ⁺ p^{1 — f} T ) ^{— ln} ( 1 ^— p^{1   f} T ) -

• II.    Автомодельное решение в чисто турбулентном режиме

При очень больших значениях числа. Рейнольдса Re «интервал энергии» и «интервал диссипации» далеко отстоят друг от друга.

В отсутствие вязкости v = 0, уравнение Кармана-Ховарта. (3) принимает вид dBLL _ £ д , 4 ) dt r4 dr rr llL -

Для замыкания уравнения (4) используется градиентная гипотеза. Ю.М. Лыткина, и Г.Г. Черных [8] для режима, колмогоровской турбулентности в инерционном интервале, выражающая момент третьего порядка B ll,l через момент второго порядка B LL:

B LLL = ² К т ^dB L , (б)

где К _т — коэффициент турбулентной вязкости. Это позволяет получить автомодельное решение для режима, чисто турбулентного движения.

Величина К _т определяется модельным выражением [9], принятым в виде аппроксимации па. основе развиваемой полуэмпирической модели переноса. в соответствии с рядом предельных соотно

Справедливы следующие асимптотики: f_T = 2 / 3

= ^exp^{( —}B^€ 1) щ >ii ^€ i ^ го; ^{1 —} f r ^ Л2 B^€ i) при € ₁ ^ 0.

В предположении существования инварианта.

Лойцянского:

по Колмогорову: uT

[6,11].

(Loi) _Т ~ и Т Л⁵ = const ,

t 10 / 7- t 0

Λ

Λ0

t ) ² / ²

• III.    Автомодельное решение в чисто вязком режиме

В режиме чисто вязкой турбулентности, т. е. предельном случае, когда, влияние вязкости становится преобладающим, согласно гипотезе Мил-лиоищикова можно положить Bll,l = 0, и уравнение (3) принимает вид dBLL _ 1 д / 4 dBLL А dt      r4 • dr V 2 v dr )■           '

Уравнение (7) замкнуто.

Существует инвариант Лойцянского:

(Loi) _V ~ и V А ⁵ = const .

Имеют место следующие зависимости:

ul _u 2₀

= t ¹ 5 1 2 • Д 0 = ^ 1? ^Л 0 = /5 ^V = 1 0' ^Г'V ^в 0 =

нольдса Re [11 u0 = (т-)   . Это соотношение u       t0

было получено при Re = го, или коэффициенте

t 0 1

= 2'

Решение уравнения (7) ищется в виде ( B LL ) _V = = u V f_v ( С ), г де £ = Г. При этом уравнение (7) сводится к обыкновенному дифференциальному уравнению d ( £ ⁵ f_V ( £ )) = d ( £ ⁴ dfd^f) ) с граничными условиями f_T[ ^ =о = 1, f_T [ ^ _ ^ = 0. Его решение f_V ( £ ) = exp ^ - 2-^ описывает предельный вязкий режим вырождения.

динамической вязкости v = 0.

Из уравнения изменения энергии dK = где скорость диссипации энергии е = (2 c )

- —е.

К 3 ^{7 2}

Д"

(2 c ) = 0.412. и инварианта. Лойцяпского и2Л5 = =   и 0Л0, т. е. K Л⁵ = K _оЛ⁵, полу чаем dK =

= ^{— (2 c} ) ^ г = ^{— (2 c} ) K 3r ( К ) / ■   Откуда.

dK _ _ К17710    и dK _        dt dt  =   (2 c) Ло К1 7 5' ILП К17710 =   (2 c) Ло К1 7 5"

Интегрируя последнее обыкновенное диффереп-

^™

IV. Коэффициент перемежаемости

циальное уравнение с разделенными перемен-иыми. получаем 10 К7710 = ^{(2 c} ) _Д0 К / 5 • ^11с'

Рассматривая взаимодействие между молекулярным и турбулентным обменами в турбулентном пограничном слое [12], JI.P. Лойцяпский, по существу, ввел выражение для коэффициента, перемежаемости:

ходя из того, что в начальный момент

Y = 1 - exp( —c i R ) ,

где c 1 — постоянш1я. параметр R = K+ Имеем

2 K+ =^^ -  *  - , ^Л

" ³ a ^{1 а} VDE 1+7^

Кт V ■

0 . 7(2 c )

0 . 7(2 c )

7 / 10

K ₀

К ^{7 7 10}

t 0

Ло К о^{1 7 5} ‘

К ⁷ / ¹⁰

K ₀

можно записать

К ₀ ^{7 7 10}    К ^{7 7 10}

——tpr . Отсюда легке) получить, что 1 — Λ0 K ₀

7 / 10

= — 0 . 7(2 c ) t—° K о¹ / 2. и.ли К 0 7 Ю = 1 +

+ 0 . 7(2 c ) t Д ⁰ K о / 2- А так ^как турбулентная энергия K = 2и² [6], то из вышеизложенного следует:

u ² ₀ u ²

1 + (2 c )1Д     - ¹ (— — 1)

2 Ло 10 t о

10 / 7

. (10)

и_т Л                   1      / t \ ² / ⁷

= —^{F ( r} ) - ^{2 F ( r} ) —5 / 7 (-)

t 0

2 F ( r )

(iT ■

Для развитого турбулентного потока из (7) получаем

Y = * - (1 - c 1 K+ ) = c 1 K+ - cF^ .   (9)

_t 3 / 7 t 0

И так как величина, коэффициента, перемежаемости y с ростом времени стремится к нулю [4], то в соответствии с (5) Loi( t ) стремится к (Loi) _V. Это согласуется с выводом Седова. [3] о том, что величина, интеграла. Лойцяпского меняется с течением времени и поэтому, вообще говоря, не может рассматриваться в качестве характерной постоянной. И только па. заключительном этапе вырождения интеграл Лойцяпского становится инвариантом, когда принимает значение, равное (Loi) _V.

V. Вырождение скорости на начальном этапе

Принято, что u_V = и_т = и о в начальный момент времени (при t = t 0). Для изучаемой модели зависимость для скорости от времени в самом начале движения (при t 0 — 1 ^ 1) можно рассматривать как следующую из колмогоровской автомодельности при большом значении числа. Рей

Из сопоставления при Re = го решений по спектру Кармана и Лыткина-Черных u0t0 = 0.351 [8]. Тогда, из (8) следует u2              t          10/7       t 10/7

Д1+(t;— 91   = (t;)   • что совпадает с соотношением Колмогорова.

Для других значений чисел Рейнольдса, в силу зависимости Re₀ = Re ^ |_t = ₁ 0 = u 0 ^ ⁰ = = uvX⁰ ' У^{Ч1ГТЫВая}- ^чт0 ^ о = V 10 Vwt- по лучим Reо = u ⁰^ = ^ Л;⁰ 1 Д Л0. Откуда U 0 t 0 = R10 (¹⁰Л0)• ^{Всл 11Ч11на} Д = Д ^(Re а ) определяется по интерполяционной зависимости обобщенной модели Кармана, для спектра. [13]. В начальный момент времени ^0 = 1 . 23 + + 0 . 0351 V Re₀ ( V Re₀ — 1). Для согласования значений постоянных и используемых аппроксимаций в выражении ^Д принято значение постоянной 0.0351 вместо 0.040 у Дрисколла, и Кеннеди. Таким образом,

Ц ^ =(^ +0 . 351 —

Ло    у Re0

0 . 351

R6;

(И)

При t0 — 1 ^ 1, раскладывая выражение в правой части (8) в ряд по степеням ( t0 — 11 и учиты- вая (11), получаем u0 = 1 + a(p - 1) ,         (12)

u ²               t 0

3             Re0

^{Д (} )V 2 12 . 3 + 0 . 351Re° - 0 . 351 V W

И при u^- = 0 . 502 (что отвечает Reo ~ 63, соответственно A = 1) из (12) получаем приближенное равенство ^ 2 ^ 1 + ( t — 1) = ^0. При иных значениях числа Рейнольдса это соотношение — приближенное. Мерой неточности может служить

Как показывают расчеты (рис. 1), значение величины (2 с ) ^/| ^ 00° • 170¹ Р^авн°й 0 • 7 Ai ^ПР^И числах Рейнольдса, превышающих 800, становится близко к единице. Тем не менее, на временах, соответствующих ( t — 1) е (0; 0 . 5), с точностью до 4% за- u ²

висимость отношения Ц- от t продолжает оставаться линейной (рис. 2). Это согласуется с предположением Бэтчелора об универсальности закона убывания энергии на начальном этапе вырождения однородной изотропной турбулентности.

продолжительность начального периода.

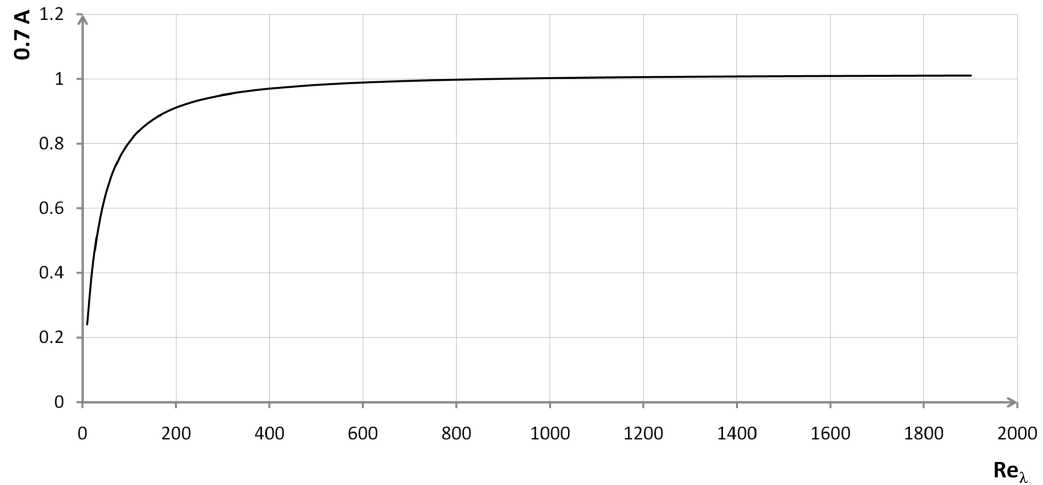
Рис. 1. Зависимость коэффициента A * 0 . 7 от числа Рейнольдса Re а

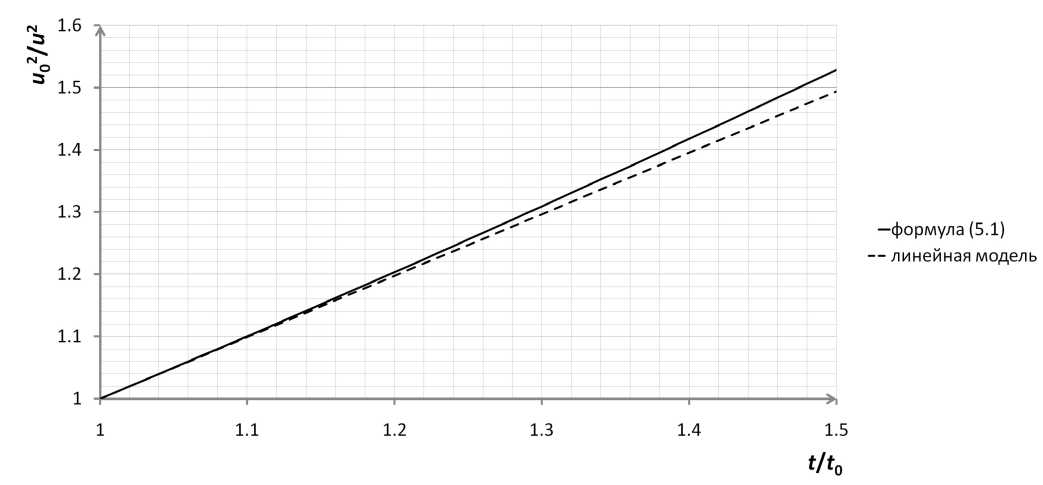
Рис. 2. Вырождение скорости на начальном этапе для Re а = 1000

VI. Дальнейшее поведение скорости

При малых значениях Re д в потоке происходит поочередная смена, турбулентного и вязкого режимов. В рамках применимости степенных зависимостей согласно принятой в настоящей работе модели из (2) и (9) получаем

u2       u2

"2 = Y • T^ + (1 - Y) •;

u20       u20

Y = Y о

'

Для чисто турбулентного режима, как отмеча-

u ²

лось ранее, справедливо -Д _u 2₀

( t/t о)¹⁰ / 7'

В те-

чепие длительного промежутка, времени

γ 0

·

( t/t о)³ / ⁷ ■ ( t/t о)¹⁰ / ⁷

u ² _u 2₀

( t/t о)¹³ ' 7'

т. е.

зату-

хание скорости пропорционально , ,¹ ,₂ ⁽ t/t о)

зави-

симости, указанной в работе [14]. С ростом вре

мени степенные зависимости становятся непри

годны, что видно по зависимости от времени t для отношения 4: 4 — > 1.23 [1]. Используя инва- ^{λ λ} t →∞

рианты Лойцянского, получаем

Ло А ⁵ / А А ⁵ 7 А о А ⁵ "Л      А О      а

∼

u

V

иД _u 2₀

(я

^ го.

_u 2₀

( t/t^/ ^{2 П141} tt o

→

Кроме того, из-за убывания со временем2 коэффициента перемежаемости (9) величина y• uT с не-u0 которого момента, времени становится меньше величины u2 =    1 5,2, т.е турбулентный режим u0      (t/t0)

затухает быстрее вязкого.

VII. Заключение

Предложенная в настоящей работе модель турбулентного потока, с перемежаемостью качественно правильно описывает вырождение скорости потока, в первые моменты времени па. начальном этапе. Тем не менее стоит отметить, что рассматриваемая модель дает лишь общий характер универсальной зависимости в ограниченном интервале времени и груба, для описания поведения потока, вблизи самой решетки.