Поверхность потенциальной энергии и термодинамические функции молекулярного комплекса H2O·O3

Комплексы и кластеры воды с кислородсодержащими соединениями и их влияние на различные физические и химические процессы, протекающие в газовой фазе, вызывают в настоящее время особый интерес в связи с проблемами атмосферной химии, климатических изменений и обеднения озонового слоя [1, 2]. Среди сложных физико-химических процессов с участием следовых газов атмосферы, протекающих в тропосфере (перистые облака) и стратосфере (полярные стратосферные и серебристые облака), а также на поверхности снега и льда в полярных областях Земли, особенно важно образование комплексов и кластеров воды с активными кислородсодержащими молекулами и, в частности, с озоном. Физическим аспектам этих процессов были посвящены обзоры [3, 4].

Вода во всех ее состояниях играет главную роль в поглощении солнечной и земной радиации и является важным парниковым газом [5]. Поскольку образование водных комплексов и кластеров вызывает сдвиг и уширение спектральных полос моно- мера в спектрах поглощения, а также ведет к появлению новых полос поглощения и повышению интенсивности запрещенных электронных переходов, водные комплексы способны изменять радиационный баланс атмосферы [6]. Это может привести, например, к искажению результатов при определении концентрации атмосферных примесей лазерными методами. Кластеры воды, участвующие в фотохимических процессах, могут также в значительной степени изменять скорости диссоциации мономера и приводить к совершенно новым каналам фотодиссоциации. Некоторые аспекты роли малых водных кластеров (в том числе, комплексов 1:1) в атмосферных процессах были недавно рассмотрены в работах [7, 8].

Химические свойства озона представляют большой интерес для многих областей химии, однако существует только незначительное число исследований, посвященных изучению его комплексов с малыми молекулами, в том числе с H2O. Результаты исследований структуры комплекса Н2О·О3, полученные методами микроволновой спектроскопии [9] и низкотемпературной матричной изоляции [10], были опубликованы практически одновременно. Найдено [9], что структура этого комплекса в газовой фазе (в импульсной сверхзвуковой струе) имеет симметрию Cs: молекула H2O и центральный атом кислорода молекулы озона расположены в плоскости симметрии комплекса с атомом водорода воды, направленным к концевому атому кислорода озона. Такая структура характеризуется противоположными направлениями дипольных моментов двух мономеров, на основании чего можно заключить, что диполь-дипольное электростатическое взаимодействие дает главный вклад в энергию связи. Этот результат был подтвержден квантовохимическим расчетом на уровне MP2/6-31G(d,p). Симметрия Cs этой структуры определяется кулоновским взаимодействием между положительно заряженным водородным атомом и двумя отрицательно-заряженными атомами кислорода молекулы озона. Энергия связи, оцененная на уровне MP2/6-31G(d), составляет 14.9 кДж моль-1 (ΔECP = 2.9 кДж моль-1), неполная оптимизация на уровне MP4/6-31G(d) (с геометрией мономера, взятой из расчета MP2/6-31G(d)) дает ΔE=10.0 кДж моль-1, ΔECP=4.2 кДж моль-1).

Иная структура (открытая конформация OOO-…H-OH с большим расстоянием O-O) была найдена впервые [11] на основе оптимизации MP4/4-31G(d,p). Хотя уровень теории, очевидно, не позволяет сделать надежное заключение о тонких энергетических различиях, авторы привлекли внимание к важному факту, что самая распространенная структура в атмосфере не та, у которой наиболее низкая энергия связи, а структура, имеющая максимально низкую свободную энергию Гиббса при данной температуре. Если различие энергии между конформациями – мало, то термодинамически благоприятнее конформация с большим расстоянием O…O.

Оптимизация геометрии комплекса 1:1 между водой и озоном на уровне QCISD/6-311++G(d,p) была выполнена в работе [12]. Расчет показывает, что три структуры abc – устойчивые формы комплекса H 2 O·O 3 . Наиболее выгодная структура H 2 O·O 3 a ) имеет симметрию C s , причем центральный кислород O 3 и всех атомов H 2 O расположен в плоскости симметрии (что близко к структуре, найденной в работе [9]). Диполь H 2 O ориентирован по направлению к центральному атому кислорода O 3 . Другие две конформации – cis и trans формы комплекса – сходны со структурами, рассмотренными в [11]. В этих конформациях все атомы расположены в плоскости молекулы, и водород H 2 O связан с одним из концевых атомов кислорода O 3 водородной связью. Энергии связи O 3 с H 2 O для дипольной, cis- , и trans- форм составляют 13.5, 8.4, и 7.9 кДж моль^-1, соответственно, на уровне QCISD/6-311++G(d,p) и 10.0, 9.5, 9.6 кДж моль^-1 на уровне QCISD(T)/6-311++G(3df,3pd)//QCISD/6-311++G(d,p). Таким образом, диполь-дипольная форма энергетически более выгодна, чем cis- и trans- конформации, которые по стабильности очень близки. К сожалению, авторы

Тачикава и Абэ не привели величину BSSE для данного расчета, которая может значительно понизить указанную энергию комплекса. Вращательные константы для дипольной формы составляют A = 11.897, B = 4.177 и C = 3.318 ГГц, что находится в хорошем согласии с экспериментальными значениями ( A = 11.961, B = 4.174 и C = 3.265 ГГц). С другой стороны, вращательные константы для cis- и trans- форм гораздо хуже согласуются с экспериментом. Эти результаты показывают, что диполь-дипольная конформация комплекса – наиболее вероятный кандидат на структуру H 2 O·O 3 , наблюдаемую экспериментально в газовой фазе [12].

Несмотря на успехи в установлении структуры комплекса озона и воды, его термодинамические функции остаются практически неизученными. Немногочисленные работы, в которых сообщалось о расчете колебательных частот и термодинамических параметрах, основаны на приближении «жесткий ротатор – гармонический осциллятор» (ЖРГО), которое, очевидно, не применимо к такой нежесткой и существенно ангармонической системе, как слабосвязанный комплекс Н 2 О·О 3 . Так, концентрационный профиль комплекса Н 2 О·О 3 в атмосфере в зависимости от высоты был рассчитан в работе [7].

Таким образом, достигнутые в последнее время результаты исследования структуры, энергетики и термодинамических функций бинарных комплексов H 2 O·O 3 , образующихся в газовой фазе при низких температурах и давлениях, нельзя считать исчерпывающими. В настоящей работе мы предпринимаем исследование структуры, энергии образования бинарных комплексов H 2 O·O 3 и полной межмолекулярной поверхности потенциальной энергии (ППЭ) квантовохимическим методом MP2, а также оцениваем термодинамические функции на основе нового оригинального метода расчета термодинамических функций, базирующегося на более точных приближениях, чем использованное ранее гармоническое приближение.

Теория и метод расчетов

Для описания термодинамических функций молекулярного комплекса H2O·O3 в данной работе используется приближение классических ангармонических ровибрационных движений / квантовых колебаний (КЛАРВ/КГК), специально разработанное для описания термодинамики слабосвязанных комплексов. В этом приближении бинарный комплекс AB рассматривается как система из двух жестких нелинейных молекул (мономеров) A и B. Набор из шести координат (α,β,γ,R,θ,φ) позволяет однозначно описать положение одного мономера относительно другого. Все возможные движения атомов разделяются на межмолекулярные движения мономеров и внутримолекулярные колебания. Межмолекулярные ровибрационные движения, спаривание между которыми не позволяет выделить отдельные колебания или вращения, представлены классическими уравнениями движения. Внутримолекулярные движения полностью независимы друг от друга и от межмолекулярных движений и описываются уравнениями движения квантового гармо- нического осциллятора, межмолекулярные движения - мгновенными значениями угловых моментов J относительных вращений мономеров, приближенно рассматриваемых как симметричные волчки, мгновенным угловым моментом комплекса L и импульсом колебательного движения мономеров относительно друг друга P. Таким образом, кинетическая энергия комплекса определяется в соответствии с формулой:

T =    J * ( A ) ²

k : 1 2 1 *

Л J ( B ) ^{2    2} L, ²    P ²

+ 2     „ +/ ' +-----

£ 2 1 *   &2 1 *  2 m A*

где IA, IB, I0 - мгновенные моменты инерции мономеров A, B и комплекса в целом, mAB – приведенная масса комплекса. Потенциальная энергия есть ангармоническая функция шести межмолекулярных координат U=U(a,в,Y,R,6,ф), определяемая путем сканирования полной шестимерной ППЭ на дискретной сетке. В узлах этой сетки энергия комплек- са определяется квантовохимическим методом, в межузельных положениях – линейной интерполяцией энергии ближайших узлов.

При использовании вышеуказанных предположений полная статистическая сумма комплекса есть произведение статсумм электронного движения, трансляций комплекса как целого, внутримолекулярных колебаний и ровибрационного движения:

Z = Z Z Z Z

0     eiclec'r'ncmVivibroi-avft ^.

Статсуммы Z elec , Z tran , Z vib определяются по стандартным формулам статистической термодинамики, аналогичным приближению ЖРГО. Стат-сумма ровибрационнго движения мономеров вычисляется путем суммирования по всем возможным энергиям фазового объема системы Q ( E ) :

₇ г d Q ( E )    Г E V

Z = --- ^^exp-- dE .

^J ₀ dE ( kT J

Классический фазовый объем при данной энергии определяется как интеграл всех возможных фазовых состояний:

Q ( E ) =     j dpdq

E < H (p, q )< E + dE и рассчитывается методом интегрирования Монте-Карло с простой случайной выборкой. После того, как статсумма комплекса Z рассчитана, термодинамические функции комплекса в состоянии идеального газа при данной температуре и давлении определяются как:

F = - k In Z

S = R In Z + RT ^{d (ln} Z ) dt

U = F + TS

H = U + RT (для трансляционных степеней свободы) H = U (для остальных)

G = H - TS .

Стандартная константа равновесия вычисляется на основе свободной энергии Гиббса образования комплекса, определенной по закону Гесса: A _bG ⁰ ( T ) = A _bE + G ⁰(T ; complex ) - ^ G⁰ (T ; monomer ) i

K ⁰( T ) = exp( -A _bG ⁰ ( T )/ RT ) .

Здесь A _b E - электронно-ядерная энергия связывания мономеров в комплексе, соответствующая глобальному минимуму ППЭ и определяемая квантовохимическим методом.

Термодинамические функции, полученные по вышеописанной процедуре, имеют погрешность, возникающую при описании квантовых ровибраци-онных степеней свободы классическими уравнениями движения. Для повышения точности классическая статсумма может быть скорректирована путем сравнения квантовой и классической статсум-мы межмолекулярных колебаний по формуле:

Z quantHO

Z corr = F Q Z classic , F Q = ”       ^.

Z classHO

Здесь F _Q - корректирующий множитель, определяемый как отношение квантовой статсуммы межмолекулярных колебаний к соответствующей классической статсумме. Эти статсуммы легко вычисляются, если известны гармонические частоты колебаний, соответствующие межмолекулярным степеням свободы в комплексе.

Описанный подход реализован в виде оригинальной компьютерной программы ADANIMEHS и применен к исследованию ППЭ комплекса H 2 O·O 3 с целью определения его термодинамических параметров. Геометрические параметры, описывающие ППЭ:

• 1.    Вращение H 2 O на угол Эйлера а (0° <  а <  360º; d α = 45º)

• 2.    Вращение H 2 O на угол Эйлера в (0° <  в <  180º; d β = 45º)

• 3.    Вращение H 2 O на угол Эйлера y (0° <  Y <  360º; d γ = 45º)

• 4. Трансляция H 2 O по оси OZ на R (2.75 А <  R <  5.50 А; dR = 0.25 А)

• 5.    Вращение О₃ вокруг оси OY на угол 6 (0° <  0 <  180°; d 6 = 45°)

• 6.    Вращение O 3 вокруг OZ на угол ф (0° <  ф <  360º; d φ = 30º).

• 116.8º. Полные энергии мономеров: E tot (H 2 O) = –76.2988008673 а.е., E tot (O 3 ) = –225.0549293698 а.е.

Дискретная ППЭ, соответствующая данной процедуре, состоит из 315 900 точек, среди которых 14 016 уникальных. Энергии уникальных точек ППЭ рассчитывались методом MP2/6-311++G(2d,2p). Для расчета энергии использовалась программа PC GAMESS [15], работающая под управлением программы ADANIMEHS. Расчет проводился в полностью автоматическом режиме, с автоматической генерацией исходных файлов и считыванием результатов. Для расчетов использовались четыре компьютера Pentium4/3 ГГц и два компьютера Pen-tium3/800 Мгц. Время расчета на компьютере Pen-tium4 составляло около 21 час (в среднем 64 с на уникальную точку, 2.28 с на 1 точку ППЭ). Расчет полной ППЭ продолжался около семи дней.

Для определения геометрии мономеров проводилась оптимизация структур H 2 O и O 3 на том же уровне расчета, что и расчет комплекса (MP2/6-311++G(2d,2p)). Геометрические параметры мономера H 2 O составляют: r (OH)=0.9583 Å, a (H-O-H) = 104.3º, мономера O 3 : r (O-O) = 1.2899 Å, a (O-O-O) =

По окончании сканирования проводился глобальный поиск локальных минимумов на дискретной ППЭ с их последующей оптимизацией на более высоком уровне квантовохимической теории.

Результаты и обсуждение

На дискретной ППЭ комплекса H2O·O3, рас считанной методом MP2/

6-311++G(2d,2p), обнаруживается 110 локальных минимумов (включая точки глобального минимума), которые классифицируются по семи типам. Их энергии и геометрические параметры приведены в табл. 1, структурные параметры показаны на рис.1. Глобальный минимум (ГМ) соответствует асимметричной структуре, близкой к той, что была найдена в [12]. Глобальный минимум соответствует межмолекулярному расстоянию R = 3.00 Å, а его структура показана на рис. 2. Полная энергия глобаль- ного минимума составляет -301.3578124128 а.е., что соответствует энергии связывания 10.72 кДж моль-1.

Полностью оптимизированная (MP2/6-311++ G(2d,2p)) структура ГМ сходна со структурой глобального минимума ППЭ (рис.2).

Для уточнения энергии комплекса были оценены величины BSSE и нулевой энергии колебаний для всех найденных локальных минимумов. Оценка BSSE проводилась стандартным методом Бойса.

Таблица 1

Структурные и энергетические параметры оптимизированных структур, соответствующих локальным минимумам (ЛМ) ППЭ системы H₂O · O₃.

Локальный минимум ППЭ	Группа симметрии	ν im , см -1	E tot , а.е.	E b ( E b +BSSE), кДж/моль	E b +ZPE ( E b +ZPE+BSSE), кДж/моль
ЛМ 1 (ГМ) ЛМ 2	C s	51 i	–301.44638263       11.83 (8.59) (перегруппировывается в ЛМ 1)		8.06 a (4.82)
ЛМ 3			(перегруппировывается в ЛМ 1)
ЛМ 4	C s	–	–301.44542875	9.33	4.66
ЛМ 5	C s		–301.44541893	9.30
ЛМ 6	C 2v	134 i , 37 i	–301.44496112	8.10	4.33 a
ЛМ 7	C 2v	63 i , 34 i	–301.44358527	4.49	3.18 a

- ТД вклад колебаний с мнимой частотой не учитывается

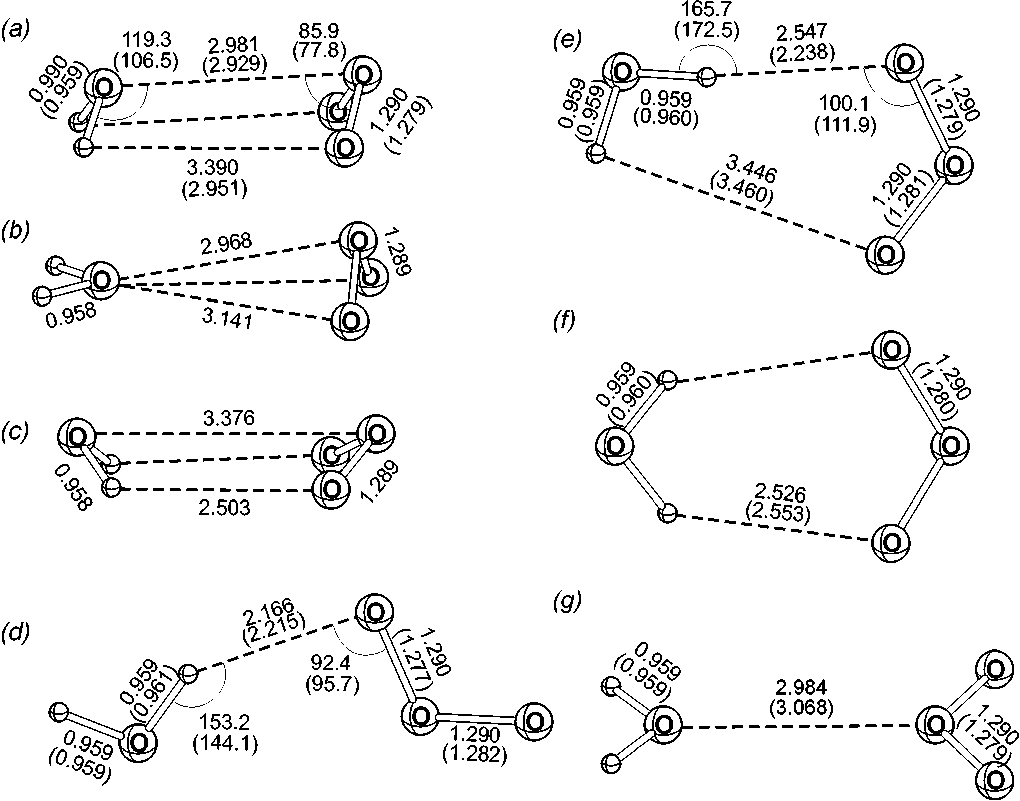
(b-g) дискретной ППЭ комплекса H 2 OO (MP2/6-311++G(2d,2p)). Значе-

Рис. 1. Структура ГМ (а) и ЛМ ния без скобок – геометрические параметры ЛМ дискретной ППЭ. Значения в скобках – результат полной оптимизации геометрии на том же уровне расчета (в случае, когда оптимизация сходится к той же структуре).

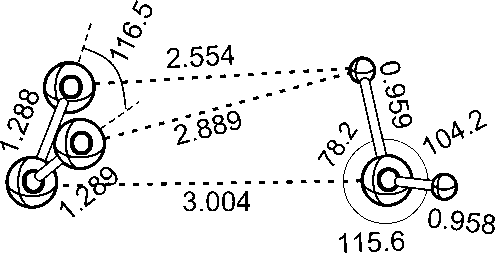
Рис. 2. Структура и геометрические параметры глобального минимума ППЭ комплекса H2O·O3, оптимизированного на уровне MP2/6-311++G(2d,2p).

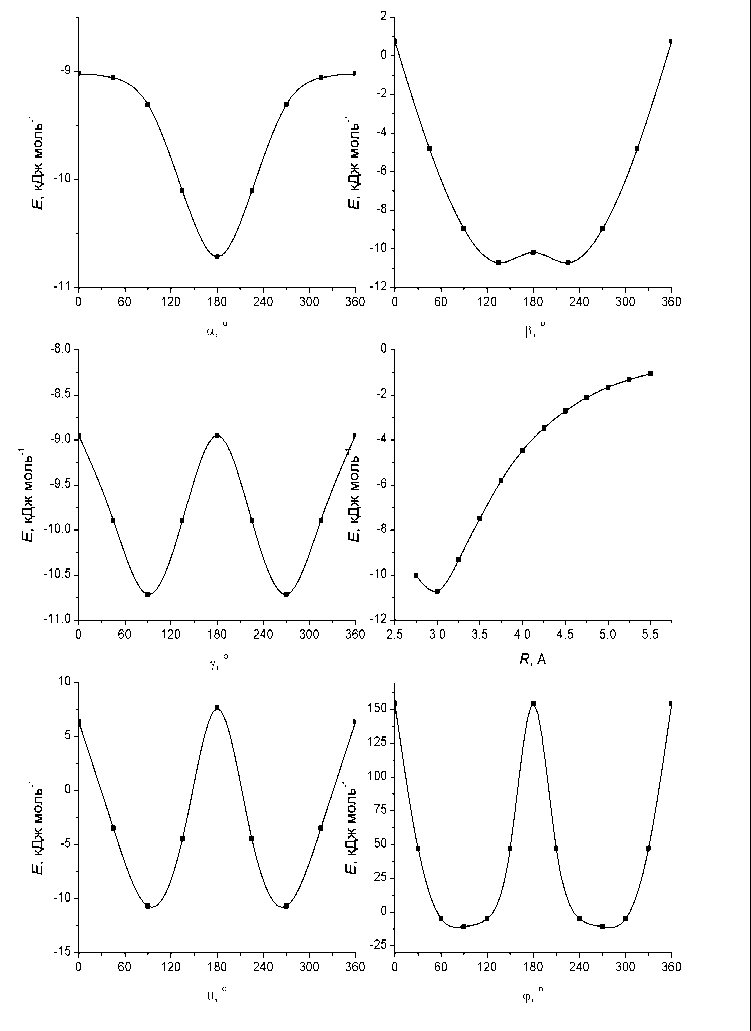
Рис. 3. Одномерные сечения ППЭ комплекса H2O·O3, проходящие через точку ГМ.

Рассчитанные полная энергия, энергия комплексообразования, величины BSSE и ZPE, а также корректированные величины энергии связи приведены в табл. 1.

Часть оптимизированных структур локальных минимумов дискретной ППЭ соответствовала истинным минимумам (отсутствовали мнимые колебательные частоты). Однако большая часть структур имела мнимые частоты, их величина обычно составляла 10-100 см-1. Такая ситуация является типичной при расчете слабосвязанных комплексов. Вследствие малой величины мнимых частот, нередко на основе результатов оптимизации, невозможно однозначно определить, является ли оптимизированная структура ложным минимумом (ошибочно найденным программой оптимизации вследствие того, что ППЭ системы почти плоская), либо мнимые частоты являются следствием численных ошибок при расчете гессиана в точке истинного, но слабовыра-женного минимума. Этот факт является еще одним аргументом в пользу использования предлагаемой здесь методики: наличие минимума на ППЭ подтверждает наличие локального минимума, даже если гармонические колебательные частоты являются мнимыми.

Рассчитанная ППЭ позволяет изучить профили ППЭ в окрестности точки глобального минимума. На рис.3 показаны одномерные профили ППЭ системы H 2 O·O 3 , рассчитанные на уровне MP2/6-311++G(2d,2p) в направлениях изменения всех координат. Как видно из приведенных данных, ППЭ системы является существенно ангармоничной, с сильным смешиванием колебательных и вращательных степеней свободы.

Для расчета термодинамических параметров данного комплекса использовалась интерполяция значений межмолекулярного потенциала линейной полиномиальной функцией по вышеописанному методу. При интегрировании по E верхний предел интегрирования составлял 50 кДж моль^-1, шаг интегрирования 0.5 кДж моль^-1. Для каждого значения E фазовый интеграл определялся методом Монте-Карло с простой случайной выборкой и подвижными пределами интегрирования по фазовым переменным, число точек интегрирования – 10000. Пределы интегрирования по R выбирались на основе предварительного анализа ППЭ для каждого значения E . Максимальное значение интервала интегрирования составляло [2.25-6.80A]. Как показывает рас-

Таблица 2 Молекулярные параметры для расчета ТД параметров реакции образования комплекса H 2 O · O 3 (расчет MP2/6-311++G(2d,2p))						плекса, используемые для расчета ТД параметров, представлены в табл. 2. Результаты расчета термодинами-
Молекулярный параметр	H 2 O		O 3	H 2 O·O 3
Спиновая мультиплетность Молекулярная масса, а.е.м. Главные моменты инерции, а.е. Число вращательной симметрии Масштабирующий фактор колебательных частот Колебательные частоты, см-1 --		1 18.0106 6.3316 4.1203 2.2112 2 0.9500 1660.9 3848.6 3974.0	1 47.9847 155.2853 137.8867 17.3985 2 0.9500 735.7 1154.0 2305.5		1 65.9953 1 0.9500 (74.8) * (92.5) (99.2) (112.5) (163.6) (245.6) 739.0 1151.8 1660.7 2298.7 3850.7 3969.0	ческих параметров при вариации параметров расчета показаны в табл. 3. Как следует из табл. 3, значения константы комплексообразования K0 комплекса H 2 O·O 3 примерно на порядок выше, чем соответствующие величины, рассчитанные в гармоническом приближении. Этот факт является следствием того, что в приближении ЖРГО учитывается только очень узкий локальный фрагмент ППЭ, непосредственно примыкающий к точке
* В скобках приведены частоты колебаний, которые соответствуют ровибрацион-ным степеням свободы в приближении КЛАРВ/ККГ. Таблица 3 Стандартные ТД параметры комплекса H 2 O · O 3 , рассчитанные в различных приближениях						глобального минимума. Оставшаяся часть ППЭ аппроксимируется квадратичной зависимостью потенциала от соответствующего геометрического параметра, причем квадратичная функция выби-
		Приближение
ТД параметр	ЖРГО	КЛАРВ/КГК (без коррекции)		Коррект.КЛАРВ/КГК ( F Q = 0.9075)
Δ r E , кДж моль-1 -8.67 -8.67 Δ r U0 (298), кДж моль-1 -0.69 -5.10 Δ r H0 (298), кДж моль-1 -3.17 -7.58 Δ r S0 (298), Дж К-1 моль-1 -67.05 -62.30 Δ r G0 (298), кДж моль-1 16.82 11.00 K0 (298) 1.13·10-3 1.18·10- чет, такой выбор параметров интегрирования приводит к попаданию в фазовый объем системы ~70% случайно выбираемых точек. Время расчета – от 10 до 40 мин (Celeron/1500 МГц) в зависимости от выбора других параметров расчета. При расчете варьировались способы выбора величины энергии диссоциации, величины гармонических колебательных частот, метод оценки кинетической энергии и метод квантовой коррекции статистического интеграла. Следует отметить, что квантовохимический расчет колебательных частот молекулы O 3 методом MP2 приводит к значительному отклонению частоты v 2 от экспериментальной величины. Однако это не приводит к существенному искажению параметров комплексообразования, поскольку величины единообразно искажаются как в случае изолированной молекулы, так и в случае комплекса. Параметры молекул-мономеров и ком-			- 8.67            летворялось единствен- - 5.20             ное условие – правиль- - 7.68             ное описание кривиз- - 63 20            ны потенциала в точке .             локального минимума. 11.16           В действительности да- 2            1.11·10-2           же при небольшом уда лении от точки минимума потенциал может иметь характер, совершенно отличный от квадратичного (рис. 3). Более того, при этом может иметь место существенно многоямный характер межмолекулярного потенциала. В итоге даже при температуре, близкой к абсолютному нулю, параметры гармонического приближения дают принципиально неверный результат. На рис.4 приведена зависимость стандартных констант комплексообразования H 2 O·O 3 от температуры, рассчитанная в гармоническом приближении и на основе интерполированной ангармонической ППЭ при явном учете ровибрационных степеней свободы (приближение КЛАРВ/КГК). Как следует из приведенных данных, величина K0 , вычисленная с учетом эффектов ангармоничости, значительно превышает результаты гармонического расчета, причем различие усиливается при

пони-жении температуры. Этот факт может иметь

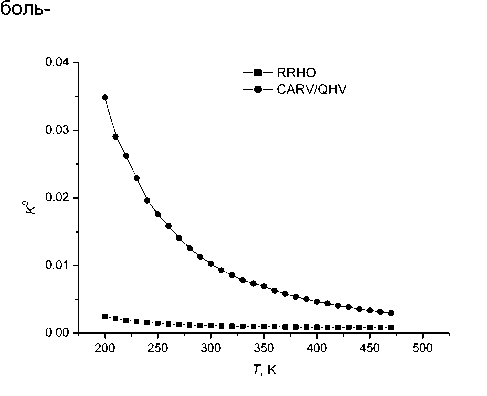
Рис. 4. Температурная зависимость стандартной константы равновесия комплекса H ₂ O ∙ O ₃ , вычисленная в приближениях ЖРГО и КЛАРВ/КГК.

шое значение при разработке современных атмосферных моделей, в которых учитывается вклад химического связывания озона в материальный или энергетический баланс.

Выводы

Впервые квантовохимическим методом MP2/6-311++G(2d,2p) исследована полная межмолекулярная поверхность потенциальной энергии слабосвязанного бинарного молекулярного комплекса озона и воды H 2 O·O 3 , включающая 315 900 точек, среди которых 14 016 уникальных по симметрии. Определена структура глобального минимума, вычислены его энергия связывания и колебательные частоты. С использованием приближения, учитывающего ангармонизм ППЭ, определены термодинамические функции данного комплекса в состоянии идеального газа, оценена его константа равновесия и ее температурная зависимость. Эти характеристики существенно отличаются от результатов расчетов, основанных на более простом приближении ЖРГО, что свидетельствует о важности учета ангармонизма при оценке термодинамических функций слабосвязанных комплексов и перспективности развиваемого метода.