Поверхностная обработка арамидной ткани и ее влияние на механику фрикционного взаимодействия нитей

PNRPU MECHANICS BULLETIN

Проблема исследования структурно-неоднородных сред не теряет своей актуальности в свете продолжающегося развития многофазных материалов, преимущества которых все больше способствуют их внедрению в конструкции для различных приложений.

Для анализа механического поведения и разрушения структурно-неоднородных сред необходимо учитывать многочастичное взаимодействие компонент и вклад каждого из них в эффективные прочностные характеристики. Как правило, многомасштабность иерархии структурно-неоднородных материалов изучается с помощью понятия представительного объема, когда размер микроструктурных неоднородностей значительно меньше размера самого объема.

В структурно-неоднородных материалах процессы деформирования и разрушения зависят от особенностей локальных полей напряжений, при расчете которых важны флуктуации и отклонения от осредненных значений, вызванные неоднородностями на микромасштабе. Распространенным направлением в микромеханике материалов со случайной структурой являются методы статистической механики для систем многих частиц, в которых для описания взаимодействия неоднородностей используются многоточечные статистики, введенные для случайных полей напряжений, деформаций и перемещений. Представленные таким образом характеристики учитывают хаотичность расположения элементов в структуре, а также дисперсию свойств фаз.

Описанию структурно-неоднородных сред при помощи инструментов статистики и теории вероятностей посвящено большое количество работ. Основные идеи предложены в работах [1–4]. Также можно выделить труды [5–9], которые посвящены методологии описания и идентификации микроструктуры неоднородных сред при помощи корреляционных функций; в работах [10–13] представлены результаты анализа свойств микроструктуры и их связи с механическими и физическими свойствами среды; влиянию параметров микроструктуры на эффективные свойства посвящены работы [14–19]. При этом отдельным вопросом является создание и идентификация точной геометрической модели микроструктуры конкретного материала [20–23].

Обзор подходов механики, использующих инструменты статистики и теории вероятностей для описания гетерогенных сред со случайным расположением включений, приведен в работе [24]. Более подробно разбор и описание методов статистического анализа микроструктуры неоднородных материалов изложен также в работах [25–29].

Неоднородность микроструктуры гетерогенного материала оказывает значительное влияние на распределение полей напряжений и деформаций в представительном объеме при нагружении. Методы и инструменты статистического анализа позволяют исследовать распределения с аналитической точки зрения для их использования в моделях механики. В таком случае, например, характеристики разрушения представительного объема и его компонент могут быть выражены в вероятностных величинах. В данной работе представлен подход, позволяющий исследовать вероятность начала разрушения отдельных фаз представительного объема на основе статистического представления критерия разрушения и восстановления функций распределения напряжений и деформаций.

1.    Вероятностное представление критериев разрушения

На основе информации о законах распределения полей напряжений и деформаций в многокомпонентной среде и ее фазах в отдельности можно получить значение вероятности начала разрушения, соответственно, среды или фаз при заданном критерии и прочностных константах. Так, в простом случае вероятность начала разрушения определяется через законы распределения компонент тензора напряжений как

^P { ° ij >° ( j^cr ) , ° ij ~ ^dist } .

Здесь о (cr ) - критическое значение напряжений (прочностная константа материала); °_у ~ dist обозначает, что напряжения распределены по параметрическому закону dist . В этом случае графический смысл вероятности разрушения – это площадь под графиком плотности распределения компоненты °_у, ограниченная слева критическим значением о ⁽c^r) (рис. 1).

В общем случае, когда, например, свойства фаз не изотропны, может быть использован более сложный критерий (критерии Хашина, Цай-Ву, Мизеса и др.). Закон распределения значений выражений для таких критериев можно получить в виде трансформации законов распределения входящих в него компонент тензоров напряжений или деформаций:

^P { F ⁽ ° у , X ° ) >  1, ° у ~ dist } , P { F ( 8 у , X _e ) >  1, 8 j ~ dist } ,

где X ° , X ₈ - совокупность критических констант, входящих в критерий.

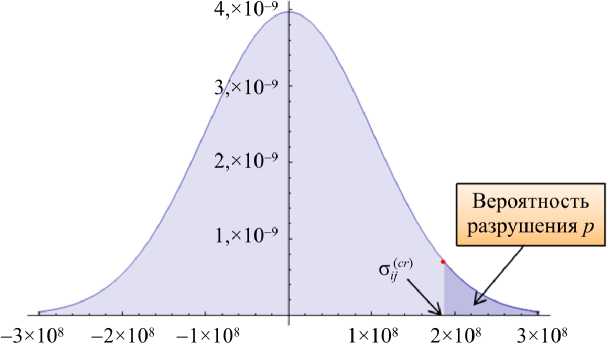
Рис. 1. Пример графического представления расчета вероятности разрушения на основе плотности распределения величины σ ij Fig. 1. A sample of a graphical representation of the probability of fracture calculation based on the density of σ ij value distribution

При рассмотрении многофазного материала подобное представление может быть введено как для каждой фазы материала в отдельности, так и для среды с эффективными свойствами. Таким образом, для оценки вероятности разрушения материала необходима оценка закона распределения напряжений в представительном объеме и его компонентах.

2.    Вычисление моментов распределения напряжений и деформаций в представительном объеме при помощи стохастических моделей

Существует несколько подходов для получения распределения полей напряжений и деформаций при нагружении представительного объема. Все они, как правило, основаны на обратном анализе распределения случайной величины с использованием статистических метрик, в качестве которых применяются, например, статистические моменты различного порядка. Таким образом, выбирается тип закона распределения, параметры которого определяются из решения системы уравнений, связывающих эти параметры и моменты случайной величины. Точность восстановления закона распределения зависит от порядка моментных функций и порядка статистических моментов. Теоретически при наличии бесконечного набора моментов n -го порядка закон распределения может быть восстановлен точно, однако при наличии ограниченного числа моментов используются гипотезы и практические данные о характере распределения.

Моменты локальных полей напряжений и деформаций в представительном объеме могут быть получены на основе различных методов, применяемых в механике композитов и неоднородных сред. Первый и наиболее распространенный способ состоит в создании конечно-элементной модели и обработке расчетных данных в дискретных элементах, принадлежащих матрице или включениям. В данном случае результат зависит от разбивки сетки, плотность которой возрастает вместе со сложностью геометрии модели. Тогда восстановление закона распределения напряжений в представительном объеме и его фазах может быть выполнено при помощи следующей процедуры. Для каждого компонента тензора напряжений, полученного для конечных элементов, соответствующих каждой фазе, строится выборка пар значений напряжений и соответствующей вероятности (весового коэффициента).

В качестве инструмента анализа полученной выборки используются моменты случайной величины либо процедура максимизации логарифмической функции правдоподобия [30].

Во втором случае статистические моменты могут быть получены из решения стохастических краевых задач с кусочно-постоянными коэффициентами [2, 3, 28, 31]. Данный подход основан на формализации информации о микроструктуре при помощи моментных функций и решении интегрально-дифференциального уравнения, содержащего функцию Грина, для получения значений отклонения полей перемещений, деформаций и напряжений от их осредненных величин. Осреднение при этом происходит по представительному объему материала. Подробно такой подход описан в работах [25, 32, 33]. Ниже приведены основные выкладки для вывода выражений для моментов напряжений и деформаций на основе решения стохастических краевых задач.

Так, флуктуация поля перемещений в представительном объеме зависит от положения радиуса-вектора и принимает вид duiX4 r ) = f dGim ( r, r )

5 x j      ^J      5 x j

mnkl

( r ) e ki + C m nki ( r i )

Nx^ r) 5 x i

, 1 n dV 1 ,

где C m _nkl ( l ) - функция флуктуации тензора структурных модулей упругости (здесь и далее апостроф ' обозначает флуктуацию величины, т.е. ее отклонение от среднего), которая в зависимости от положения радиуса-вектора характеризует ту или иную фазу материала. В данном случае флуктуация характеризует отклонение от средних по представительному объему модулей упругости C_mnkl . Нагружение задается при помощи тензора e_kl деформаций представительного объема как единого целого. G_im ( г , Г ) - функция Грина, с помощью которой получено решение краевой задачи. Согласно определению такая функция удовлетворяет равенство

C^G ,,., ( Г - Г ) = -$ . 8 ( r - Г ) .                               (4)

Для неограниченной среды существует функция Грина в виде тензора Кельвина-Сомильяны:

G mk ( Г , r ) = A ^ I ^{r - r} 1l

( r m — r i m ⁾⁽ rk — r i k )

Поскольку размеры рассматриваемых представительных объемов намного меньше размеров конструкций, объем можно считать неограниченной средой. Константы A и B зависят от упругих свойств фаз материала [34, 35].

Структура уравнения (3) позволяет находить решения в итерационном порядке, подставляя решение, полученное на предыдущей итерации, в правую часть. В первом приближении флуктуациями перемещений в правой части пренебрегают, и решение сводится к следующему виду:

Uu ’( r ) = e„ J G .,,, ( Г. l ) ( C m.. (Г ) ) , i , ^J 'i . (6)

• V 1

Флуктуация тензора структурных модулей упругости определяется через индикаторную функцию ф(C)(r), поле ненулевых значений которой определяется положительным присутствием фазы C в координатах, заданных аргументом (радиусом-вектором). Таким образом, для двухфазного материала флуктуация тензора модулей упругости сводится к следующему виду:

C' ,ki ( r W I ( r ) ( C ijkl -C iM¹ ) ,                              (7)

где C C = X₍ C ) 8 -j 5 ki + U₍ C ) (⁸ .k ⁸ Ji ^{+ 8} -i ⁸ Jk ) ; I ^- фаза включений; M ^- матрица; X C c ) и ц₍ с ) ^— константы Ламе.

Для численного решения краевых задач в виде интегральных уравнений (6) необходимо найти способ интегрирования сингулярности, вносимой знаменателями в слагаемых функции Грина (5). Один из методов, который используется в разных вариациях стохастического подхода, предполагает, что для нахождения решения уравнения (6) могут быть использованы вторые производные функции Грина, переход к которым осуществляется с использованием математического преобразования Стилтьеса.

Такая трансформация была выполнена в [3] с целью разложить интеграл по второй производной функции Грина на две составляющие – сингулярную, представляющую из себя постоянный тензор, и формальную, интегрирование по которой происходит по всему интервалу, за исключением сингулярности и прилегающей к ней окрестности. В работе [3] для двух этих частей были выведены точные выражения. Преобразование Стилтьеса двух функций f(x) и g(x) по интервалу (a, b) определяется как bb

^ ( t ) = f f ( t — x ) g ' ( x ) dx = f g ( t — x ) f' ( x ) dx .                       (8)

aa

Такая операция позволяет «переместить» дифференцирование с флуктуаций структурных модулей упругости на функцию Грина. С учетом тождества (8) в упругом случае решение в первом приближении будет иметь следующий вид:

u '⁽ 1 ( ^r ) = euC_mnki f G_im ( r, - ) ф' ( - ) dV\ . i , j       kl mnkl   im , jn    111

V 1

Сингулярная и формальная составляющие второй производной функции Грина

^G.m , jn ( r, ^- ) = ^Gk ) is ( r, ^Г ) ^{+ G}fis ( ^r , ^- ) , полУченНые В [3], имеют вид

( ^s ) /r -X    ^{8 (} r r l ⁾fc$?     ¹       ^ X/rr\

^Gkf : is ( r , r i ) =—з^^⁸ kf ⁸ is - 5 ^k8 kfis J=⁸ ( r - r i ) g kfis ,                 ⁽¹⁰⁾

G kf , is ⁽ r, r i ) = ₈    | Г   - P ( ⁽ 2 ^{- k) 8} kf' ( 3 n f n s ^{- 8} fs ) ^-

8 пц | r - r 1 ^x

^-K[ ³ ( n kf n is ⁺ n ki n fs ⁺ n ks n fi ⁺ n fs n ki ⁺ n fi n ks ) ^{- 2} I kfis ^{- 15} n knfnlns ] ) ,

к =

X + u --------, n i =

X + 2 ц

r - r.               - 1 „

| r - ^-| , n J = nn j , I kfis = 2 ⁽⁸ ki ⁸ fs

+ 8 ., 8 f ) .

e J ( r ) = 2 ( u ‘ _j ( F ) + u j _z (F ) ) первый и второй моменты поля деформаций в представительном объеме как среде с эффективными свойствами записывается через решение (3) в виде

⁸ J ⁽ r ) e ij ,

8' I F Кр ( F ) =

= 1е_ие ,С ,.С Jf( G Ar,r *) + G Ar,r i))x

• * kl ф h mnkl УПФ h J J \ im , J V , 1/       jm,i \ , 1//

4                      V 1 V 2

x d ² K ^{( 2 )} ( F. F )

x(С,, (r, r) + G„,.(r, ,))—■       dV2 dVi, dx n dx 2n где k[2)(F, F )= фI^ F), фI (r2) - моментная функция второго порядка случайной величины фI (F), характеризующая корреляцию значений функции в точках, удаленных друг от друга на расстояние |F - г|. В данном случае моментные функции флуктуаций индикаторной функции описывают морфологические особенности внутренней геометрии представительного объема.

Моменты первого и второго порядка полей деформации также могут быть получены для отдельных фаз представительного объема [2]:

( Jc = e.+ A- e«C- К Gm,j( r, r) + Gj„,( Г, F ))8K^(Г,r) d V(14)

2 pC         Vi

{⁸ j ^{( r} ) ⁸ aP ^{( r} )) _C = (⁸/ / - ^{( r} ) ⁸ aP ^{( r} )) ⁺ e ij e _ap -(ф / -^ (⁸ «P ^ ⁺

+—«Ф C (r )8j( r )8;6( r))+е5(ф C (r )8;6( r))+e„(Ф C (r )8j( r)».

Моменты первого порядка полей напряжений в фазах могут быть получены через соотношение

(J   = C ^{( C} )£

^U ijC   Z/ky H ⁸ klC •

С учетом упругой постановки задачи и линейной связи между напряжениями и деформациями моменты второго порядка полей напряжений c j ( r ) с^ ( r ) C могут быть вычислены на основе полученных по формуле (15) моментов второго порядка полей деформаций.

3.    Восстановление законов распределения случайных полей

Как было показано, представленная стохастическая модель дает возможность вычислять центральные моменты случайных полей. Параметры законов распределения аналитически связаны с моментами случайной величины, для каждого закона распределения эта связь имеет свой вид. Соответственно, для восстановления закона распределения полей деформаций или напряжений необходимо решить обратную задачу: найти такие па- раметры, которые соответствовали бы распределению с центральными моментами, полученными с помощью решения краевой задачи.

При конечно-элементном моделировании распределение полей может быть получено на основе анализа выборки элементов, среднее значение полей в которых попадает в тот или иной диапазон значений. Для восстановления распределений по результатам конечно-элементного анализа используются средства пакета Wolfram Mathematica.

Для иллюстрации методик восстановления законов распределения были исследованы модели представительных объемов пористых неоднородных материалов c малой объемной долей.

Рассмотрим представительный объем структурно-неоднородной среды со сферическими полидисперсными частицами. Трехмерная геометрическая модель такого объема представляет из себя куб (матрица) со случайно расположенными непересекающимися сферами разных размеров (включения). Матрица обладает изотропными упругими характеристиками: E M = 7 х 10¹⁰ Па, v M = 0,35 . Включения представляют из себя поры, свойства которых с целью корректности математической постановки задач задаются ненулевыми, но в разы сниженными по отношению к матрице: E I = 1 Па, v I = 0,3 . Объемная доля включений составляет 5 %. Нагружение задано в виде растягивающих перемещений u 1 = 10 ^{- 5} м по оси 1. Геометрия представительного объема отображена на рис. 2, а .

При использовании стохастической модели информация о морфологии микроструктуры учитывается в виде совокупности моментных функций, входящих в интегральные выражения (13) и (14). Для реализации алгоритма получения значений моментных функций (подробно изложен в [31]) используется воксельное разбиение представительного объема, представленное для исследуемого частного случая на рис. 2, б . В данной работе результаты, полученные при помощи стохастической модели, приведены в сравнении с результатами конечно-элементного анализа, выполненного на той же воксельной сетке.

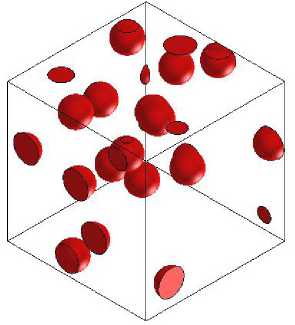
а

Рис. 2. Представительный объем ( а ) и воксельная сетка для него ( б )

Fig. 2. Representative volume ( a ) and voxel mesh for it ( b )

б

Для рассмотренного примера в качестве моделей распределений, используемых для восстановления распределения полей напряжений и деформаций, были исследованы нормальное распределение, косое нормальное распределение, и гамма-распределение. Нормальное распределение определяется параметрами масштаба и сдвига, при косом нор- мальном распределении добавляется параметр формы, а при гамма-распределении – два параметра формы. Функции плотности этих распределений имеют следующий вид: нормальное распределение

1           ( x -a ) 2

в 72 Л exp - 2 _P 2

где в >  0 - параметр масштаба; a - параметр сдвига;

косое нормальное распределение в 72л

exp

^^^^н

к ( х -н

(х -и)1 :

2 в . 1

_ t 2

e ² dt ,

где в >  0 - параметр масштаба, a - параметр сдвига, к - параметр формы; гамма-распределение

9 к - 1

( х -a ) exp

х -a

I в )

где в >  0 - параметр масштаба; a - параметр сдвига; к >  0 , 9 >  0 - параметры формы.

Исходная гистограмма разброса вероятности значений компоненты о_п напряжений в матрице, полученная на основе конечно-элементного моделирования на воксельной сетке при шаге нагружения и 1 = 2 х 10 - 4 м, представлена на рис. 3. Поле значений о_п напряжений представлено на рис. 4. Графики функции плотности вероятности для трех выбранных законов распределения отображены на рис. 5. Параметры распределений представлены в таблице.

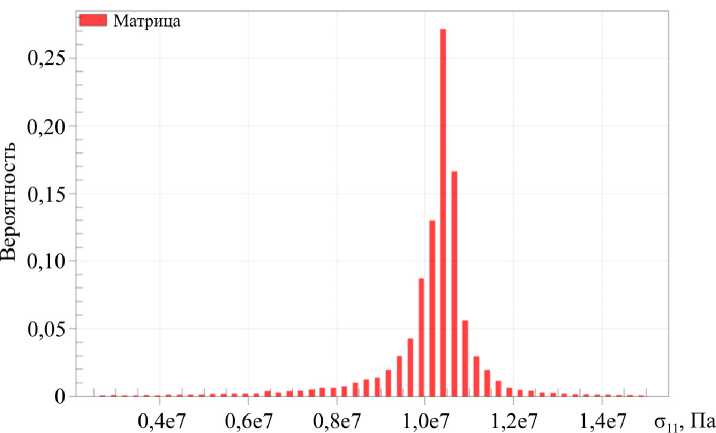
Рис. 3. Разброс вероятности значений компоненты о_и напряжений в матрице по результатам конечно-элементного моделирования Fig. 3. Probabilities of о ,, component values of stresses in the matrix according to the results of finite element modelling

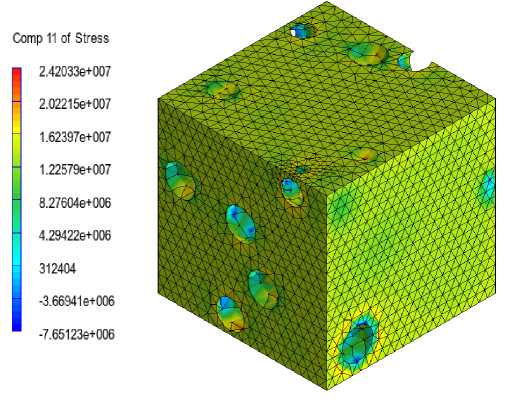
Рис. 4. Значения компоненты напряжений о 11 в матрице пористого представительного объема Fig. 4. Values of о 11 stresses component in the matrix of the porous representative volume

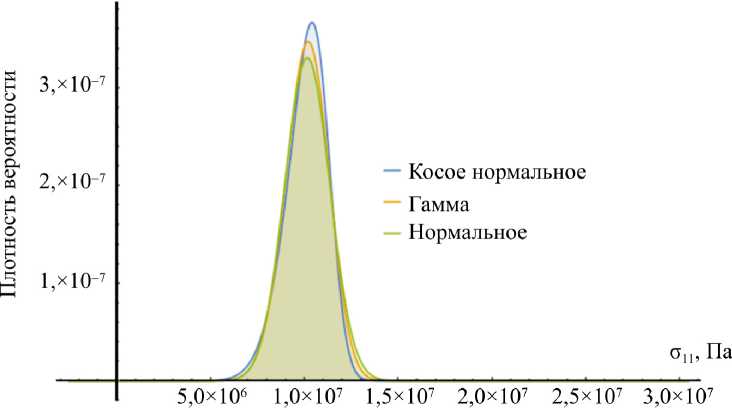
Рис. 5. Плотность распределения вероятности для компоненты 11 тензора напряжений в матрице

Fig. 5. Density of probability distribution for component 11 of stresses tensor in the matrix

Параметры законов распределения напряжений а_п на шаге нагружения и = 2 х 10 ^{- 4} Parameters of laws of stress distribution o_n at a loading step u 1 = 2 х 10 - 4

Параметр	Распределение
	нормальное	косое нормальное	гамма
Параметр сдвига a	1,015 х 10 7	1,127 х 10 7	12,21
Масштабный параметр p	1,207 х 10 6	1,641 х 10 6	7,147 х 106
Параметр формы k	–	- 2,115	4,695
Параметр формы 9	–	–	4,200

В общем случае из-за несимметричности функции плотности вероятности необходимо использовать многопараметрические распределения (косое нормальное, гамма, Вейбулла и др.), для определения которых в рамках стохастического моделирования необходимо как минимум три центральных момента. Из результатов видно, что в рассматриваемом примере распределение значений напряжений близко к нормальному закону. В этом случае для определения параметров распределения на основе результатов стохастической модели достаточно первых двух центральных моментов (среднего значения и дисперсии).

Для полученных законов распределения напряжений о_п в матрице можно получить зависимость вероятности разрушения от значения критической константы о ( Сr ) (рис. 6).

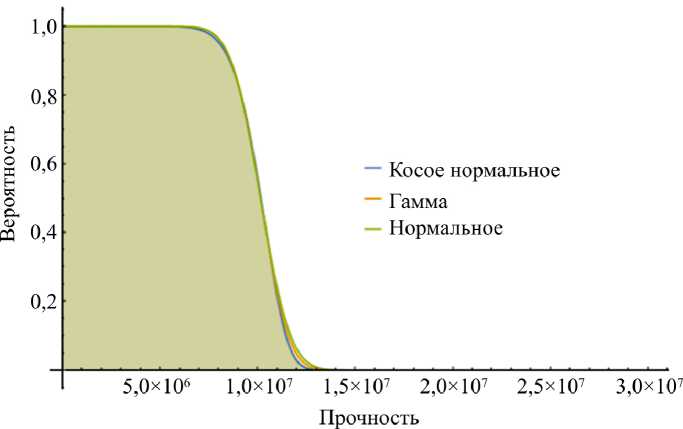
Рис. 6. Значение функции вероятности выполнения критерия в зависимости от предела прочности о^ r) для матрицы Fig. 6. Value of the probability function of the criterion depending on the yield value ст'"' ) for the matrix

4.    Расчет вероятности разрушения при статическом нагружении

На основе ключевых положений предложенной методики можно реализовать стохастическую модель прогрессирующего разрушения. Тензор структурных модулей упругости C jkl ( r ) зависит от радиуса-вектора и является кусочно-постоянным в представительном объеме:

С„ ( г ) =₉ ( г ) Cj + ( 1 -ф ( r ) ) j .                     (20)

Если принять, что вероятность разрушения равна отношению объема разрушенных элементов в представительном объеме к представительному объему целиком, то после осреднения получаем

(C_MH ( r )) = pD,^ + ( 1 - p ) D_MC$ ),                       (21)

где вероятности разрушения включений D_I и матрицы D_M определяются по формуле (2). При моделировании накопления повреждений в рамках стохастической модели происходит деградация свойств матрицы и включений за счет увеличении вероятности разрушения фаз на каждом шаге нагружения.

Для рассмотренного в предыдущем параграфе частного случая представительного объема было проведено моделирование прогрессирующего разрушения на основе конечно-элементной и стохастической упругой модели при использовании критерия максимальных напряжений (1) и значении критической константы о^ ) = 2,1 x 10 7 Па. На рис. 7 представлен график напряжения-деформации в матрице, полученный при помощи двух моделей.

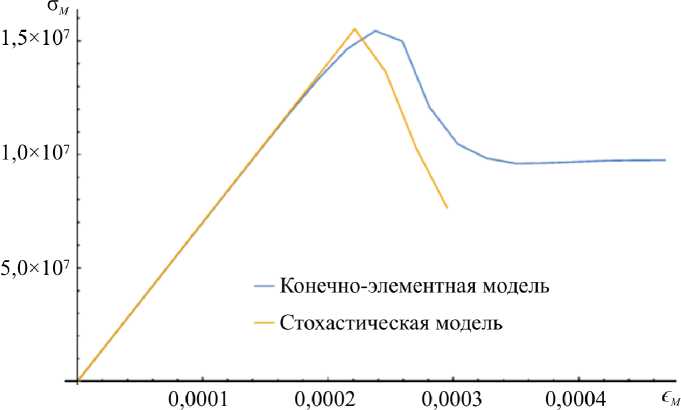
Рис. 7. Зависимость напряжений от деформаций в матрице Fig. 7. Dependence of stresses on deformations in the matrix

Несмотря на то, что в упругой области модели дают идентичный результат, стохастическая модель имеет более выраженный обрыв на графике. Это связано с точностью численного решения интегральных уравнений в стохастической модели и разбивки сетки при конечно-элементном анализе, а также с шагом нагружения. На графике матрица начинает разрушаться до того, как среднее значение напряжений достигнет критического значения, поскольку обе модели оперируют осредненными величинам – в стохастической модели осреднение происходит по кусочно-постоянным функциям, а в конечноэлементной по объемам элементов.

Выводы

В данной работе представлен подход, позволяющий восстанавливать законы распределений полей напряжений и деформаций в компонентах представительного объема и вычислять на их основе значения вероятностей разрушения фаз представительного объема при заданных критериях и прочностных константах. Рассмотрены численные примеры.

В общем случае описанная методика позволяет восстановить функции распределения всех компонент тензора напряжений, что позволяет вычислять вероятность разрушения с использованием более сложных критериев, комбинирующих в себе прочностные константы материала и значения компонент тензоров напряжений или деформаций.

Cтохастический подход может быть использован для исследования степени влияния разброса параметров микроструктуры и констант неоднородной среды на прочностные характеристики материала [36]. Для оценки прочности всего представительного объема на основе вероятности микроразрушения существует ряд подходов, позволяющих установить связь между вероятностью разрушения микрокомпонент, количеством разрушенных микрочастиц, а также экспериментальными данными. Так, вводя параметры, определяемые экспериментально для каждого материала, можно получать соотношения, напрямую связывающие вероятности микро- и макромасштабного разрушения. Существуют также подходы, основанные на базовых математических теориях, таких как теория перколяции [37] и теория пучка [38]. Критерии для компонент, представленные в виде законов распределения тензоров напряжений и деформаций, могут соответствовать тому или иному механизму разрушения, что позволяет использовать модель разрушения с совокупностью критериев.

Работа выполнена при поддержке гранта Президента Российской Федерации для государственной поддержки молодых российских ученых – кандидатов наук (МК-2395.2017.1), а также Российского фонда фундаментальных исследований (проекты 16-01-00327_а, 16-41-590259-р_а).

Acknowledgments

The work was carried out with the financial support from the Gant of the Russian Federation President aimed at the State Support of Young Scientists, PhDs (MK-2395.2017.1), as well as the Russian Foundation for Basic Research (Projects 16-01-00327_a, 16-41-590259-р_а).