Поверхностные интегралы

Которая называется интегральной суммой первого рода для функции f(x,

y,

z).

d = max ^

Если при (где ) существует предел интегральных сумм, который не зависит от способа разбиения поверхности S на части и выбора точек Mi, то этот предел называется поверхностным интегралом первого рода и обозначается ii/cx.y^da:

s

Если функция f(x, y, z) непрерывна, то интеграл

JH/c^zzw существует.

Определение поверхностного интеграла первого рода аналогично определению криволинейного интеграла первого рода. Свойства поверхностного интеграла первого рода (линейность, аддитивность и т.д.) также аналогичны соответствующим свойствам криволинейного интеграла первого рода.

Если поверхность S задана на области D плоскости Оху функцией z=z(x,y), причем z(x,y) непрерывна, вместе со своими частыми производными z’x= z’x(x,y) и z’у = z’у(x,y), то поверхностный интеграл сводится к двойному с помощью формулы:

|| /(x,y,z)dCT = || J(x,y,z(x,y))^K+Vj + ^y* dxdy.

Если поверхность S задана параметрически в виде , где x, у, z – непрерывно дифференцируемые функции в некоторой области G плоскости то

\\J(x,y,z)dcr = \\ Дх(и,и),у(и,и),г(и,и)^^[Ён^^dudu, где

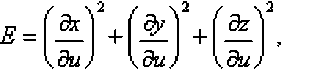
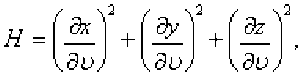
Приложения поверхностного интеграла первого рода

Пусть S – гладкая материальная поверхность с плотностью . Пусть с помощью поверхностных интегралов первого рода можно вычислить: 1) статические моменты этой поверхности относительно координатных плоскостей

Мху = 11 zpdo, Myz = 11 xpdcy Mxz = 11 ypda;

s

s

• 2)    координаты центра тяжести поверхности

М щ   _ М ту m Zc m где

• 3)    моменты инерции относительно координатных осей и начала координат

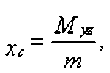
s

,

,

,

.

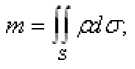
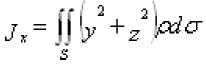
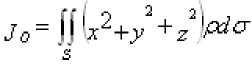
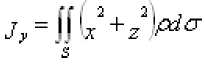
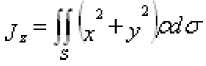
Определение и вычисление поверхностного интеграла второго рода

Площадь поверхности S можно найти по формуле:

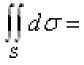
пл.S.

Если Р^{1 К}-У’²¹ - поверхностная плотность материальной поверхности S, то ее масса m находится так:

™ = 11 p(x,y,z)dcr.

Пусть S - гладкая ориентированная поверхность, на которой задана непрерывная функция ^'^у,^', и пусть в каждой точке M поверхности определено положительное направление нормали ^R<^, (к(М) — непрерывная вектор-функция).

Выберем ту сторону S+ поверхности S, для которой угол между единичной нормалью ” и осью Oz острый. Теперь разобьем поверхность S на части S1,...,Sn c диаметрами d1,...,dn. Обозначим через ^Pv’^P_a площади соответствующих проекций частей S1,...,Sn на плоскость Оху, а через d -максимум из чисел d1,...,dn.. Выбрав в каждой части Si произвольную точку Mi(xi, yi, zi), составим сумму

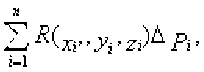
которая называется интегральной суммой второго рода для функции ^x,y,z\ Предел интегральных сумм (он существует в силу непрерывности ^Р-У-²) ) при d s 0, который не зависит от способа разбиения поверхности S на части и выбора точек Mi, называется поверхностным интегралом второго рода от функции ^«У*²! по поверхности S и обозначается

11 R

Аналогично определяются поверхностные интегралы второго рода

11 R(x,у ,z) dydz H R(x,y,z)dxdz.

и от непрерывных функций Р^.У^ и Q^,y,z) . Сумма трех указанных поверхностных интегралов второго рода называется общим поверхностным интегралом второго рода и обозначается

• 11 Pdydz + Qdxdz + Rdxdy.