Поверхностные явления в жидкостях

Поверхностные силы в граничных слоях и тонких пленках классических молекулярных систем необходимо учитывать при описании различных физико-химических явлений, протекающих вблизи ограничивающей поверхности: адсорбция, смачивание, жидкости в наноразмерных полостях. В этом случае молекулярная система имеет аксиальную симметрию, для которой применима модель жидкости, граничащей с твердой идеально гладкой поверхностью.

Другой круг задач относится к системам со сводной границей раздела фаз, например, переходный слой жидкость – пар (жидкость – кристалл) и т. д. Однако и в этом случае, в силу огромной разности концентраций вещества по разные стороны границы раздела фаз, модель жидкости, граничащей с твердой идеально гладкой поверхностью, является хорошим начальным приближением.

Особенностью модели является необходимость учета граничного условия перехода от аксиальной к сферической симметрии вдали от ограничивающей поверхности, где жидкость является пространственно однородной и изотропной. В свою очередь, свойства молекулярной системы со сферической симметрией полностью обусловлены парными молекулярными корреляциями, убывающими с расстоянием между частицами как потенциал взаимодействия U(r) (обычно как r ^-6 ).

Более сложная ситуация наблюдается в квантовых системах, для которых парные корреляции существуют даже в идеальном газе при отсутствии межмолекулярного взаимодействия и убывают с расстоянием как r–4. В том случае, когда размеры системы существенно превышают длину корреля- ции l0, детали межмолекулярного взаимодействия становятся несущественными. Именно поэтому осуществляется перенормировка потенциала в теории ферми-жидкости. Однако в том случае, когда l0 сравнимо с размерами системы (тонкие пленки и нанокапли жидкостей), детали межмолекулярного взаимодействия и, соответственно, ближний порядок необходимо учитывать. Для описания этой компоненты межмолекулярных корреляций также можно использовать модель жидкости, граничащей с твердой идеально гладкой поверхностью.

В работе мы ограничиваемся рассмотрением классических молекулярных систем в рамках модели жидкости, граничащей с твердой идеально гладкой поверхностью (стенкой).

Основные уравнения

Статистическое рассмотрение молекулярной системы обычно основывается на уравнениях ББГКИ (Боголюбова – Борна – Грина – Кирквуда – Ивона) или других, эквивалентных им интегральных и интегродифференциальных уравнениях для l -частичных функций распределения ^G 1,..., l ⁼ ( ^{r r} 1 ^{,..., r r} l ) ансамбля N тождественных частиц, находящихся в заданном объеме V и взаимодействующих друг с другом посредством потенциала Ф ij (r ij ), где r ^{ij =} r ^{i -} r ^j – расстояние между центрами частиц i, j . Характерный размер каждой частицы равен σ . Бесконечную зацепляющуюся систему уравнений ББГКИ можно преобразовать в систему всего двух точных интегральных уравнений, называемую фундаментальной системой уравнений Орнштейна – Цернике (ОЦ) для одно- и двухчастичных функций распределения. Эти функции являются наиболее важными, поскольку описывают структуру и позволяют рассчитать термодинамические параметры вещества. Все высшие функции распределения могут быть однозначно выражены через них. Трудности в решении фундаментальной системы связаны с тем, что данные уравнения содержат бесконечные функциональные ряды от искомых функций распределения (бридж-функции, представляющие собой бесконечные суммы неприводимых диаграмм). Просуммировать аналитически или вычислить численно с необходимой точностью такие ряды не удается. Для решения конкретных задач приходится вводить дополнительные физические предположения и аппроксимировать бридж-функции некоторыми аналитическими выражениями (замыканиями), что приводит к приближенным интегральным уравнениям, которые можно представить в форме ОЦ.

ω1 = n ∫ G2 C12(1)d(2) + ln a, h12 = C12(2) + n ∫ C12(2)h23d(3),                                         (1)

здесь интегрирование ведется по координатам i -й частицы d(i) ≡ dr i ; n – плотность; G i = exp (-Ф i /kT + ω i ) – однoчастичная функция распределения, описывающая положение частицы в лабораторной системе координат; Ф i – потенциальная энергия частицы во внешнем поле; ω I – одночастичный термический потенциал, учитывающий влияние окружения на данную частицу; α – коэффициент активности, определяемый обычно из условия перехода к пространственно-однородной системе; h ij = = [exp (-Ф ij /kT + Ω ij ) – 1] – парная корреляционная функция, связанная с двухчастичной функцией распределения соотношением G ij = G i G j, (1+h ij ); Ω ij – двухчастичный термический потенциал, учитывающий опосредованное взаимодействие двух частиц через их окружение; С_i j^(k) – прямые корреляционные функции:

C ij ⁽¹⁾ = h ij – ω ij – 1/2h ij ( ω ij + M ij⁽¹⁾ ),

C ij ⁽²⁾ = h ij – ω ij + M ij⁽²⁾ ,                                                 (2)

в которых M_i j^(k) – бридж-функционалы, представляющие собой бесконечные ряды неприводимых диаграмм. Подобные ряды не могут быть просуммированы в окончательной форме, поэтому на самом деле формально точные уравнения системы (1–2) являются незамкнутыми, например, второе связывает две неизвестные функции, h(r) и C(r).

Существенно, что система уравнений (1–2) допускает обрыв бесконечных рядов неприводимых диаграмм, стоящих в ее правой части без появления по крайней мере явных противоречий, которые возникают в случае преобразования цепочки уравнений ББГКИ к системам приближенных интегральных уравнений [1–3]. Именно поэтому теория жидкости, основанная на решении обобщенной системы уравнений (1–2) для одно- и двухчастичных функций распределения, – одна из наиболее полных и строгих.

Особенно большое значение для теории жидкостей и газов имеет случай пространственно-→→ однородных изотропных сред, в которых: G1 (r) ≡ 1 и ω1(r ) = 0. В результате первое уравнение системы (1–2) вырождается в определение избыточного химического потенциала:

ц = ln a

n J C 1(2 ) ⁽ r 12 V

) dr ₁₂

Второе уравнение определяет единственную неизвестную функцию:

h 12 = C 12(2) + n J C 12⁽²⁾ h 23 d (3).                                        (4)

Для пространственно-однородных, изотропных систем (объемные жидкости при отсутствии внешних полей и вдали от ограничивающих поверхностей) имеем G ₁ ( r ) = 1 , G₁₂ ( r , r ₂ ) = G ₁ ⁽ 0 ⁾( r ₁₂ ) . Все структурные (ближний порядок) и термодинамические параметры выражаются только через двухчастичную функцию распределения G 12⁽⁰⁾ (r 12 ), параметрически зависящую от приведенной плотности n = N/V -o ³ . Существующие в настоящее время численные методы позволяют вычислять эту функцию с высокой степенью точности (~2 %), хотя ряд принципиальных вопросов не решен до сих пор.

Пространственно-неоднородные системы (жидкость в контакте с твердой поверхностью) описываются двумя функциями распределения - G1 (r) и G12 (r, r2) Граничным условием является переход вдали от ограничивающей поверхности к объемной жидкости lim G12 (r, r )= G10(r12 ) .

Г 1 ^Х, r ^Х

G 1 ( Г Ь 1 , ^r 1 ^Х

Г 12 =| r - r |= const

Знание этих функций позволяет рассчитать микроструктуру жидкости [4–6] – локальную плотность и ближний порядок, а также все макроскопические характеристики: поверхностное натяжение, адсорбцию, расклинивающее давление и т. д.

Синглетное приближение

Непосредственное решение уравнений (1–2) для функций многих переменных, даже в случае простых систем сферически симметричных молекул, требует больших численных расчетов. Упростить задачу можно, если вместо двухчастичной функции G12 (r1, r2) использовать, в соответствии с (4), ее граничное значение G12(0)(r12), для объемной жидкости – так называемое синглетное приближение. В результате получается замкнутое уравнение для одночастичной функции распределения G1 (r), описывающей профиль локальной плотности n(r1 ) = nG1(r1) вблизи твердой поверхности. Численное решение уравнения приведено в работах [7].

Разумеется, полное пренебрежение изменением ближнего порядка жидкости вблизи твердой ограничивающей поверхности не позволяет непосредственно из уравнений определить погрешность синглетного приближения. Как правило, эту погрешность оценивают сравнением результатов расчета с эталонными данными численного эксперимента. В работе мы уточним синглетное приближение, частично учитывая изменение ближнего порядка в уравнениях для функций G ^{1 (} r¹ ) и G ^{12 (} r¹, r² ) .

Сформулируем теперь уравнения для молекулярной системы, соприкасающейся с твердой непроницаемой поверхностью. Начало отсчета совмещаем с центром частицы, соприкасающейся с поверхностью; ось z направляем по нормали (рис.). В результате жидкость заполняет все верхнее полупро- странство z > 0; нижнее полупространство z < 0 недоступно для движения молекул.

Такая пространственно неоднородная система обладает аксиальной симметрией, в силу которой

^G 1 ⁽ r ) = ^G 1 ⁽ z 1 ) = exP ⁽ ® 1 ⁽ z 1 )) ,                   G 12 ⁽ r , r ) = G 12 ⁽ z 1 , z 2 , r 12 ) ,                     (6)

где r₁₂ - расстояние между центрами произвольной пары частиц; z ; >  0 - удаление каждой из i -ой частиц от поверхности. Отметим, что если все расстояния измерять в единицах характерного размера частицы о , то r₁₂ ^(m;n) = 1, z₁ ^(m;n) = 1/2, что отражает факт непроницаемости частиц и твердой стенки. Функции G 1 и G 12 являются решением системы уравнений (1–2) с заданными граничными условиями, которые в соответствии с (5) имеют вид

Рис. 1. Аксиальная симметрия для одночастичной функции распределения

® 1 ^{( z} 1 ) ^ 0,               G 1 ( ^z 1 ) ^ 1,               G^^{0 (} r_n ) = lim G₁₂ ⁽ z i , z 2 , r_X2 ),                  (7)

21^^                           Zj^to                                          Zi^1», Z 2^да r2 =1Г- r2l = const

Отметим, что наиболее просто система уравнений (1–2) решается в упоминавшемся выше синглетном приближении [4], которое принимает вид tot = n J G2C 12(1,0)d(2) + In a,                                         (8)

h 12⁽⁰⁾ = C 12⁽2,⁰⁾ + n J C 13⁽2,⁰⁾ h 23⁽⁰⁾ d (3).                                      (9)

Решение второго уравнения, как упоминалось выше, решается независимо для объемной жидкости. В результате для расчета одночастичной функции распределения достаточно решить только одно уравнение: прямая корреляционная функция C 12^(1,0) (r 12 ) считается известной. Именно поэтому приближение называется синглетным (одночастичным).

Выход за рамки синглетного приближения

Изменение ближней молекулярной системы, граничащей с твердой поверхностью, происходит при сколько угодно малых плотностях. Продемонстрируем это на примере разреженного газа: в этом случае одночастичный и двухчастичный термические потенциалы можно находить посредством разложения в степенной ряд по плотности [8–11]. Ограничимся разложением с точностью до первого по- рядка

,

.

Подставляя (10) в (8, 9), получим выражения для коэффициентов разложения

"Р5^/**^

где f ij – функции Майера, интегрирование (+) ведется по всему верхнему полупространству, константы ц ⁽ⁱ⁾ определяются из граничного условия на бесконечности. В частности, в первом порядке по степеням плотности есть двухчастичная функция распределения однородной жидкости вдали от ограничивающей поверхности. Если устремить координаты z 1 , z 2 к бесконечности, то to ₁ ⁽¹⁾ (z₁) стремится к нулю, а to _1z ⁽¹⁾ стремится к своему сферически симметричному выражению mJ'^R^OO - R 1z² ).

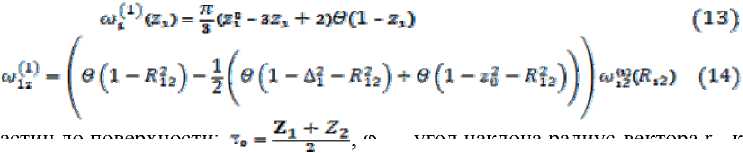
to 1z⁽¹⁾ (R 1z ) = 2 n /3(R 1z² -3R 12 +z).

где z1, z2 - расстояние от частиц до поверхности;             , ф1z - угол наклона радиус-вектора r1z к оси z, R1z = r1z/2, 0(z) - функция Хэвисайда. Заметим, что

Таким образом, полученное решение описывает переход от аксиальной к сферической симметрии при стремлении каждой из частиц молекулярной системы к бесконечности.

Термодинамические величины

Упоминавшиеся выше макроскопические величины – коэффициент адсорбции и поверхностное натяжение – вычисляются следующим образом to

Г = V }( G 1 ( Z 1 ) - 1 ) dZ 1

,

to Г                    \

/ = J| P _N - — ^р т I dZ 1

ЬI a J

где P N и P _T - нормальная и тангенциальная компоненты тензора давлений, в=1/кТ

P ?_N = VG 1 ( z ) - V t ddr_n ^Z-^ в и]¹ d a G 12 ( z -

V          2 V ²        r 12 dr 12 ₀

or>^{N       N} r ^P 2 ^dP^

P P _T = —G 1 ⁽ z ^)-       d^r 12------ d ^{a G} 12 ⁽ z

V          4 V ²         r 12    dr 12 0

a z 12 ,

^^^^^^в

a z 12 ,

В частности, для вычисления адсорбции достаточно разложения одночастичной функции до первого порядка по степеням плотности

G 1 (z 1 ) = exp( ω 1 (z 1 )) ≈ 1 + n ω 1⁽¹⁾ (z 1 )

N ^∞          N π

Г = V n ∫ ω ₁ ⁽¹⁾ ( z ₁ ) dz ₁ = V n 4

Обсуждение результатов

Продемонстрировано, как для разреженной молекулярной системы, граничащей с идеально гладкой поверхностью, осуществляется граничный переход от аксиальной к сферической симметрии. Решение получено посредством разложения искомых функций в ряд по степеням плотности с точностью до линейных слагаемых. Упоминавшемуся выше синглетному приближению соответствуют формулы (13), (15), что связано с допущением, что твердая поверхность не вносит возмущения в двухчастичное распределение. В нашем подходе осуществлен выход за рамки синглетного приближения: возмущение, вносимое твердой поверхностью в двухчастичное распределение, вычисляется по формуле (14). Аналогичным способом можно получить разложения с точностью до второго порядка, что соответствует газу средней плотности. Однако для жидкости такой метод неприемлем, и поэтому необходимо строить аппроксимацию в область высоких плотностей, как это сделано в работе [9].