Поверхностные SH-волны в преднапряженных пьезоэлектриках с функционально-градиентным покрытием

PNRPU MECHANICS BULLETIN

Проблема распространения поверхностных акустических волн является одной из актуальных проблем современной механики. С одной стороны, это связано с широким спектром приложений в акустике, геофизике, сейсмологии, дефектоскопии и др., с другой стороны, с бурным развитием технологий создания новых пьезоэлектрических материалов с уникальными, ранее не наблюдавшимися в природе свойствами. Возможность создания на их основе принципиально новых типов электронных приборов и устройств обусловило значительный рост работ, посвященных математическому моделированию процессов распространения волн в функционально-градиентных средах [1–6]. В [1] построена общая теория электродинамики сплошной среды, приведены основные типы термодинамического потенциала, предложены подходы к построению линеаризованных соотношений динамики преднапряженной электроупругой среды. В [2–4] приведены определяющие соотношения динамики сплошной пьезоактивной среды при наличии начальных механических или электростатических полей. В [5–7] дан вывод определяющих соотношений динамики упругой и пьезоактивной среды в произвольной, в общем случае криволинейной системе координат. Особенности распространения сдвиговых волн в слоистых преднапряженных средах рассмотрены в [8–12]. В [8–11] изучено влияние начальных напряжений на скорости распространения волн Лява и Гуляева-Блюштейна. В [12] изучены вопросы распространения волн в слабо неоднородных средах, неоднородность которых обусловлена наличием начальных напряжений или поляризации. Показано, что при специальных условиях в слабо неоднородном полупространстве могут возникать вторые моды поверхностных волн типа волн Гуляева-Блюштейна. В [13–16] исследуются процессы распространения волн в функционально-градиентных пьезоактивных средах, параметры неоднородности которых допускают построение аналитического решения в той или иной форме. В [13] исследованы особенности распространения волн Гуляева-Блюштейна в среде, все характеристики которой изменяются по одному и тому же закону. Рассмотрены случаи полиномиальной и экспоненциальной зависимостей. Исследовано влияние параметра неоднородности на скорость, дисперсию, коэффициенты затухания, глубину профилей, электромеханический коэффициент связи. В [14] исследованы особенности распространения волн Гуляева-Блюштейна в среде, характеристики которой изменяются по специальному, допускающему аналитическое решение закону. Изучено влияние параметра неоднородности на характеристики волнового поля. В [15] изучаются волны Лява в среде из поляризованной керамики с функционально-градиентным покрытием. Для построения аналитического решения используется асимптотический подход. Исследовано влияние параметра неоднородности на дисперсионные соотношения, в частности на фазовые скорости поверхностных волн, а также на электромеханический коэффициент связи. В [16] изучается влияние параметра неоднородности и начальных напряжений на характеристики волнового поля.

В настоящей работе предложена модель сегнетоэлектрической структуры, состоящей из однородного пьезоактивного полупространства с неоднородным покрытием, представляющим собой либо слой, либо пакет однородных или функционально-градиентных пьезоактивных слоев. Предполагается, что полупространство, равно как и покрытие, находятся в условиях воздействия начальных механических напряжений, свойства покрытия описываются произвольными функциями. Для этого случая система дифференциальных уравнений с переменными коэффициентами специальной заменой сводится к системе начальных задач Коши. Функция Грина строится численно на основе использования процедур Рунге-Кутты с модификацией Мерсона, которая позволяет эффективно контролировать погрешность вычислений. При построении функции Грина сегнетоэлектрической структуры с неоднородным покрытием использован матричный подход, позволяющий сочетать аналитические и численные методы построения отдельных ее составляющих. В рамках линеаризованной теории электроупругости в работе исследованы особенности распространения поверхностных волн в сегнетоэлектрических гетероструктурах с учетом различного характера механических воздействий на составляющие структуры. Изучено влияние величины наведенной деформации, вида и характера преднапряжений в составляющих структуры на особенности поведения и скорость распространения поверхностных акустических волн (ПАВ) для ряда наиболее востребованных сегнетоэлектриков. Установлены условия, при которых действие начальных механических напряжений приводит к увеличению скорости волны Гуляева-Блюштейна относительно скорости исходного материала, а также условия, при которых пьезоэлектрическая структура перестает быть слабо неоднородной.

1. Постановка задачи

Рассматривается задача о распространении сдвиговых горизонтально поляризованных волн, движущихся в направлении x1 по поверхности составной преднапряженной пьезоактивной среды. Полагаем, что колебания среды вызваны действием удаленного ис- точника гармонических колебаний, среда представляет собой однородное преднапряжен-ное полупространство x2 < 0, | x11, | x3| < ^ с преднапряженным покрытием (рис. 1 а, б).

Рис. 1. Геометрия задачи Fig. 1. Geometry of the problem

Покрытие моделируется либо одним слоем 0 <  x 2 <  h = H (см. рис. 1, б), либо пакетом x 1 |, x 3 h k _{+ 1}< x 2 <  h k , k = 1,2,..., M - 1 как однородных, так и неоднородных слоев из функционально-градиентного материала. В качестве исходного материала структуры используется пьезоэлектрик класса 6 mm гексагональной сингонии, ось симметрии которого в естественном состоянии (ЕС) совпадает с осью x ₃ , векторы поляризации составляющих покрытия и полупространства совпадают либо противоположны по направлению. Начально-деформированное состояние (НДС) каждой из составляющих структуры однородно и наводится за счет действия начальных механических напряжений, внешние начальные электрические воздействия отсутствуют [1–7, 17]:

R = r ■ Л, G = Л ■ Л^т, Л = 5 _zvv_z r _z r j , v_z = const.                     (1)

Здесь R, r – радиус-векторы точки среды в начально-деформированном и естественном состоянии соответственно; vz = 1 + 5z, 5z - относительные удлинения волокон, направленных в естественной конфигурации вдоль осей, совпадающих с декартовыми координатами; 5^- - символ Кронекера. Неоднородность начального напряженного состояния составляющих структуры вызвана только неоднородностью физических свойств. Исследования проводятся в лагранжевой системе координат, совпадающей с прямоугольной декартовой системой, режим колебаний полагается установившимся, динамический процесс удовлетворяет условиям u1( n) = u 2( n) = 0, -^- = 0, uk (n) = uk (n) (x1, x2), u 30) = 0, k = 3,4, n = 0,1,2,..., M.         (2)

dx ₃

При этом для слабо неоднородной пьезоэлектрической структуры (см. рис. 1, а , б ) в ЕС выполняются соотношения:

для однородных составляющих [6, 7]

_p < - ) =_p ( M ) , c 0( ⁿ ) = _Cj 0 ( ^M ) , e_ 0< n ) = e 0 ( ^M ) , _E »( n ) =_E 0( M ) либо e [< . ) =_ e 05 ^M ) .             (3)

для неоднородных составляющих [12]

Р^М =Р 0 M ⁾ / р ' " ’ ( x 2 ) , C ij ⁾ - ^‘"^ЧX 2 ) , e j ⁾ - ^fn ⁾ ( X 2 ) , s j ') -s jM f ( n ⁾ ( X 2 ) .      (4)

Далее используем безразмерные параметры: линейные параметры отнесены к харак терной толщине к-го слоя

l ' - l ( h 0 ^{k )} )

плотность - к плотности полупространства

' ( ” )        ( ” ) ( M )

рv ' - pv ' / Ро \ упругие параметры - к модулю сдвига подстилающего полупространства cjn) = cj) / c04M). При переходе к безразмерным параметрам пьезоэлектрических и диэлектрических констант используется множитель £- 1010 В/м, при этом ej(n)= ej^ / c44M), sjn)-sinW /c44M) (s'° — диэлектрическая проницаемость вакуума). Далее штрихи опускаем.

В качестве безразмерной частоты используется либо параметр к2 -to h / VSM), либо к2e -toh / VSeM) (где VSM) = -Jc44M) / p0M) - скорость сдвиговой волны полупространства и VM) = J( c44M) + e0M)2 / s^M)) / p0M) - скорость сдвиговой волны полупространства с уче том пьезоэлектрических свойств в ЕС [18]).

В рамках принятых предположений краевая задача о колебаниях преднапряженной электроупругой среды x ₂ <  H описывается линеаризованными уравнениями [6-7, 12]:

V ₀ • 0 ⁽ n ) =р ₀ ⁽ n ) u ⁽ n ) ,

V0 • A(n)= 0, для вакуума x2 > H

Аф ^{( 0} ) = 0

с граничными условиями на поверхности :

отсутствие механических воздействий:

n • 0("|x,=H = 0, электрически свободная поверхность:

n • A(1) I „ = n • A(0) I „ , ф(1) I „ = ф(0) I „ x 2 = H              x 2 = H ,         x 2 = H          x 2 = H металлизированная поверхность:

Ф")! x,= H = 0, на границе раздела сред (i = 1,2,..., M -1)

ue(i)l h = ue(i+1)U , n • 0 (i)l h = n • 0 (i+1)l, , n • A (i)l h = n • A(i+1)l, I x 2 - h                     I x 2 -hi                       I x 2 -hi'                           I x 2 -hi                        x2 - hi                            x2 - hi на бесконечности ue(M)| x2 . . 0, ue(0)| x2 . . 0.

Здесь V0 - оператор Гамильтона; ue(n) = {u3n\ u4n) = v(n)} - расширенный вектор переме щений; n - вектор внешней нормали к поверхности среды определены в системе коорди нат, связанной с естественным состоянием (ЕС); р0(n) - плотность материала а2     a2

n-составляющей в ЕС; А = —2 +--2" - оператор Лапласа. Верхний индекс «(n)» соответ- дx12 дx 2

ствует номеру среды, составляющей структуру ( n = 0 - вакуум, n = 1 - поверхностный слой, n = M - полупространство). Линеаризованные тензор напряжений 0 ' ⁿ ) и вектор индукции А ^{1 n} ) с учетом (1) представляются в виде [12]

0(n) _ с(n)*(n) , е(n)*(An)     n(n) - ДnУ(n) _ е(n)*(D(n)

Vlk = clkspus,p + elkp V,p ,   Dl = elsp us,p blp V,p , где       c(n)* _ O(n)§   ,v(n)v(nуn)x    1n)* _ v(nуn)   £(n)* -£ v(n)v(n)v(nn))2g  + r(n)

где       clksp = Plp Oks + Vk Vs clksp ,  elsp  = Vs elsp , fclp Ь0Ч  V2 V3  (Vl )  Olp +elp .

Участвующие в (14) компоненты тензора Кирхгофа p pn ) , а также упругие константы c lnp зависят как от свойств материала, так и от вида начального напряженного состояния среды [1, 6, 7, 12]:

р ^{( n} ) -1 _с ^{( n} )§ /У^{( n} ) )²_й  2 ⁿWⁿ ) +15 5 _c ^{( n} )   f[_v^{( n} ) )²_й f[_v^{( n} ) )²-Й

^Plp 2 c qjlp ^O qj ( ( ^V q ) 1 )    e jlp W j ¹ 8 ^O mn ^O qj c mnqjlp ( ( ^V q ) 1 )( ( ^V m ) 1 ) ,

_c ⁽ n )x _ a x^   _ c ⁽ n ) ,¹ c ⁽ n ) r ,⁽ n ) _ c ⁽ n ) ,¹ о _c ⁽ n ) n ) )²_i^

c qjlp a r ( n ) a 5 *( n )     c qjlp ' 2 c mnqjlp^mn c qjlp + 4 m'c>im'qnpl ( ( ( ^V m ) 1 ) ^.

Здесь использована упрощенная запись термодинамического потенциала x [1, 6, 7]:

_v ^{( n} ) _ ¹ Дⁿ ) е( ⁿ ) ( ⁿ ) (nⁿУ[Л7⁽ⁿ ) e( ⁿ ) ¹ r^{( n}Ул7⁽ⁿ )И7 ^{( n} ) ¹ (nⁿ ) V^{( n} ) ^{( n} ) ^{( n} )

^X = C qjkq fl djqj^k l ^- e jkl W j ⁵kl “TP qj W q W j ⁺ -c mnqjkl ^ mn ^ q j ⁵kl , 2                        2             6

где S ^^{n )} - компоненты тензора деформаций Коши в случае однородной деформации (1) определены формулами

S(" '= V2»j((v,<" ))2-1), где Wjn) - компоненты материального вектора электрической индукции; cqnk и c'imnqjkl -упругие константы II и III порядка; Р^,) - константы диэлектрической восприимчивости, связанные с константами диэлектрической проницаемости соотношениями

£^{( n} )=£5 +В^{( n} )

^ь kp ^ь 0 ^о kp ^+e kp •

Для удобства дальнейшего изложения введем обозначения

⁶ lksp = c lksp , ⁶ lk 4 p = v k e pk , ⁶ 1 4 sp = v s el sp , ⁶ 1 44 p = ^-£ lp , k , ^l , s , p = ^1,2, 3.           ⁽¹⁶⁾

Подставляя выражения компонент тензора напряжений и вектора индукции (13) с учетом (2), свойств (3), (4), обозначений (16) в (5)-(12) для преднапряженных однородных составляющих структуры, получаем (индексами после запятой отмечены производные по соответствующим координатам)

О( n ) J n ) ₊0( n ) J n ) ₊0( n ) J n ) ₊0⁽ n ) J n ) -_o⁽ n ) ^d u 3

v 1331u3,11 + v2332u3,22 + v1341 u4,11 + v2342u4,22   p0 2 л , d t

0(n) Jn) + 0(n) Jn) + 0(n) Jn) + 0(n) Jn) - 0 u 1431 u 3,11 + ^2432 u 3,22 + v1441 u 4,11 + v2442 u 4,22 V’ для преднапряженных функционально градиентных составляющих

3 2 (

0⁽ n ) _M⁽ n ) +0⁽ n ) // n ) +0⁽ n ) ,/ n ) +0⁽ n ) // n ) +0⁽ n ) ( nn )₊0⁽ n ) _M⁽ n ) -_D⁽ n ) ^d u ³

^v 1331 u 3,11 ^{+ v}2332 u 3,22 ^{+ v}1341 u 4,11 ^{+ v}2342 u 4,22 ^{+ v}2332,2 u 3,2 ^{+ v}2342,2 u 4,2    ^p 0 ^ t 2

0⁽ n ) J n ) ₊0⁽ n ) J n ) ₊0⁽ n ) J n ) ₊0⁽ n ) J n ) ₊0⁽ n )  J n )₊0⁽ n )  J n ) -0

v 1431 u 3,11 + v2432 u 3,22 + v1441 u 4,11 + v2442 u 4,22 + v2432,2 u 3,2 + v2442,2 u 4,2 v, для вакуума

U(0) + u(0) =0 u 4,11 + u 4,22 0, граничные условия

₀(i)|            ' ()"^: //"^: ■ ()"^: z/") II =0

^w23 x 2 = H   I   2332 u 3,2 ^{+ v}2342 u 4,2 || x 2 = H   ^v,

>(*)|            ' o") //l|: I о") у/") '         =r>(0)l = Ге(0)

u?| x 2 = H = u 4 ^0|| x , . H , (21)

2 | x 2 = H   | ^u2432 u 3,2 ^{+ u}2442 u 4,2 J| x 2 = H   ^2 | x 2 = H   | ^v2442 u 4,2 J| x 2 = H ^

U 4"| x 2 . H = 0,                                             (22)

u e ⁽ m >L = u e ⁽ m ⁺¹⁾l „ , ®₂₃ ⁽ m ’L-, I ^x 2 - h m                |^x 2 - h m      ²³ |^x 2 = h m

-®J m ⁺¹⁾| „ , D _? ⁽ m )| „

²³ |^x 2 h m ² | ^x 2 h m

= D ⁽ m ^{+ 1 )} I

^D 2       |x 2 = hm ’

u^{e l} “ 'I x 2 ^-. ^ 0, ф ^|0) | , 2 ^. Ф 0.

В рамках настоящей работы исследуем две краевых задачи о распространении поверхностных горизонтально поляризованных волн в преднапряженных пьезоэлектриках с покрытием [1, 6–12]:

задача I – со свободной поверхностью, описывается уравнениями движения (17)–(19) с граничными условиями (20), (21), (23), (24);

задача II – с металлизированной поверхностью, описывается уравнениями движения (17)–(19) с граничными условиями (20), (22)–(23).

• 2.    Решение краевых задач. Дисперсионное уравнение для преднапряженного пьезоактивного полупространства с преднапряженным покрытием

При решении краевых задач I и II используем преобразование Фурье по координате x ₁ , a - параметр преобразования. Движение пьезоэлектрической структуры в трансформантах Фурье имеет вид:

для преднапряженных однородных составляющих

0(n) и(n)"_fa20(n) _D(n)K2>j7у(n)+0(n) u(n)"_a20(n) u(n)=0 v2332U 3     (a u1331 p K 2 )U 3 +V2342U 4 a U1341U 4

p⁽ n ) tj⁽ n )" — r/²A⁽ n ) T7⁽n ) -u A⁽ n ) T7⁽n )" — r/²A⁽ n ) T7⁽n ) — A-

• u2432U 3 a V1431U 3 + V2442U 4 a V1441U 4

для преднапряженных функционально градиентных составляющих

0( n ) u⁽ⁿ )"-fa²e⁽ n ) -o⁽ n ) k²1 t/⁽ n ) + e⁽ n ) u⁽ⁿ )"-a²e⁽ n )t/⁽ n ) + e⁽ n ) ^fu^ⁿ )' + 9⁽ n ) ⁽u^k n ⁾‘=o

• u2332U 3     (a v1331 p  K2)U 3 + V2342U 4 a V1341U 4 + v2332 U 3 + v2342 U 4

  
  

n^{( n} ) tt^{( n} )" _ ^2n( ⁿ ) tt^{( n} ) _|_ a^{( n} ) tt^{( n} )" _ г,²a^{( n} ) tt^{( n} ) _i_ A^{( n} ) ⁽T7^^{n )f}-i-A^{( n} ) ⁽T7^^{n )f} — A-

• ^u2432 U 3 ^{a U}1431 ^U 3 ^{+ V}2442 ^U 4 ^{a V}1441 ^U 4 ^{+ v}2432 ^U 3 ^{+ V}2442 ^U 4 0;

  для вакуума

  
  

  U 4^{0 )} '' - a ² U 4^{0 )} = 0,

  
  
  
  

  с граничными условиями

  0 F ^{( 1 )} I

  23 |x 2 = H

  
  

  = 0 ^{( 1 )} ^у⁽¹⁾' ₊ 0^{(1 )} ^y^{( 1 )} ' I _ 0 ^v2332 U 3   ^{+ V}2342 ^U 4     |x ₂ = H   0,

  
  
  
  

  D 2 F ⁽%

  U Ц x 2

  
  

  x 2 =.

  
  

  ₌  0 ^{( 1 )}   [/^{(1 )} ' ₊ 0^{(1 )}   u^' I       = D F ^{( 0 )} I       =  6^{(0 )} D^{(0 )} '   I

  I     ^u2432 U 3 ^{+ U}2442 ^U 4     |x ₂ = H   ^2     |x ₂ = H     ^U2442 ^U 4    |

  = и ^{( 0 )} I

  ^U 4 | x 2 = H ,

  
  

  x 2 = H ,

  
  
  
  

  u ^{( 1 )} I       = 0

  U 4 | x 2 = H   0,

  u e ⁽ m )i        = и e ⁽ m ^{+ 1)}i        , ₀ F : m )i        _=@ F : m ^{+ 1)}i , _d f ⁽ m )i        = _d f ⁽ m ^{+ 1)}i

  I ^x 2 = h m                 |^x 2 = h m ’ ²³     |^x 2 = h m        ²³        |^x 2 = h m , ²       |^x 2 = h m        ²         |^x 2 = h m

  U e ' " )l x 2 .-. 1 0 . U 401 | x 2 ,. 1 0

  
  
  
  

  ^,

  
  
  
  
  
  

Решение задач (25)–(27) с граничными условиями (28)–(32) в трансформантах Фурье для однородных составляющих покрытия ищем в виде ( p = 3,4, n = 1,2,..., M - 1 ) [6, 7, 12]

^U(p ) ^{( a} , x 2 ) = V ^fk ) [ c kn ) ch ^k ) ^x 2 ⁺ c k + 2 s^h ^k ) ^x 2 ] , k = 1

для неоднородных составляющих

U(p )(a, x2 ) = V ckn)Л)(a, x2 ), k=1

для полупространства и вакуума

Up" )(a, x2) V f". CkM k=1

' e °" ) ^{x 2}, U 4^{0 )} ( a , x ₂) = r e ^-a x 2

.

Участвующие в представлениях (33), (35) o kn ) удовлетворяют характеристическому уравнению det M ⁽ _c ⁿ ) ( o ^{( n} ) ) = 0.

m ( ” > ( 0 n ) ) =

¹2nL ( о^{( п}' )^г - ( a ² e | П 3, -P ^{( n |} K 2 ) 6 2 n 42 1 °. ⁿ ) -a ² e |34,

0^{( n} )       ⁿ )\² _„²0^{( n} )

⁶ 2432 ( ° ) ^{a 6} 1431

0⁽ n ) Mn )\² _„² 0⁽ n )

⁶ 2442 ( ° ) ^{a 6} 1441

.

Коэффициенты f ^n ) определяются из решения однородной системы линейных уравнений с матрицей коэффициентов M ⁽ _c ⁿ ) ( o j n ) ) . y p ) ( a , x ₂ ) в (34) - линейно независимые решения задачи Коши с начальными условиями y kП ) ( a ,0 ) = 5 _kp для уравнения

Y ^{( n )} ' = M ^{( n )} ( a , x 2 ) Y ^{( n )} , Y ^{( n )} =

Σ n

n

, XE

F ^{( n} ) ^ 23

Г) F ^{( n} )

n

, _u

U ( ⁿ )

U 4 ⁿ ) ,

0                0           а 2 ^{o (} ” 31 -р ⁽ n ) ^К 2 а 2 ^{o (} ” 3

О                О               а 20⁽ n ⁾         а²0⁽ n ⁾

v               v              ^а V1431        ^а V1₄₄

-< ( g 0 Г¹   о^ ( g 0 у¹        0         0

О& ( g 0 ) ^{- 1}      o n ( g 0 )'           0             0

„ -о^{( n} ) а^{( n} ) -(й^{( n} ) V g 0 ^u2442^v2332 ( ^v2432 ) ^.

Следует отметить, что при построении функции Грина для электроупругой среды с неоднородным покрытием могут быть использованы различные и весьма эффективные подходы [19–23]. В настоящей работе использован предложенный в [24] подход, сочетающий аналитические решения (33), (35) для однородных с численными методами для неоднородных составляющих структуры, в частности, при решении систем (37), (38) применен модифицированный метод Рунге-Кутты.

Неизвестные Ckn) (33)-(35) определяются из удовлетворения граничным условиям (28), (29), (31), (32) для задачи I или (28), (30)–(32) для задачи II. Следуя [24] представим дисперсионное уравнение задач в виде det A = 0, (39)

' B ^{( 1 )} ( К) G" ) ( h_iy . A ^{( 1 )} ( h 2 M ) B ⁽ M ) ( h M ) .

Размеры матрицы A и матриц ее составляющих определены геометрией задачи и условиями на поверхности.

Задача I : матрицы A и A ^{( 1 )} ( h _{2 M} ) - квадратные, размер определяется геометрией задачи и равен соответственно 4 ( M - 1 ) + 3 и 4 ( M - 1 ) . B ^{( 1 )} ( h i ) , B ⁽ M ⁾ ( h M ) и G ^{( 1 )} ( h i ) -матрицы размера 3 x 4, 4 x 3 и 3 x 3, вид которых полностью определяется свойствами верхнего слоя, подстилающего полупространства и диэлектрической проницаемостью вакуума соответственно и не зависит от свойств и количества возможных промежуточных слоев.

	" 0	0	0 >		M l 11
G ( 1 ) ( h i ) =	0	0	-£ ( 0 ) а	, B ( M ) ( h „ ) =	M 21 M
	0	0	- 1		f 31
	k		>		M k f 41

M

M

^M f ₃₂

M f 42

0 )

для преднапряженного однородного поверхностного слоя

	1* 1* ' и " о	1* 1* l 12 s 21	1* 1 l 11 c 11	1* 1 l 12 c 21
B ( 1 ) ( h 1 ) =	1* 1* 1 21 " 11 Y	1* 1* 1 22 "  21 Y	1* 1 1 21 c 11 Y	1* _1 1 22 c 21 Y
	k Л\ c 1 1 Y	f42 c 21 Y	110 f 41 " 11 Y	1 „10.. f 42 "  21 Y J

для преднапряженного функционально градиентного поверхностного слоя

0„(1)      „(1)      „(1)      „(1) ^ y11     y12     y13     y14 B|1|( hi) = (1)              (1)              (1)              (1) y2 1)y y22)y у2л y24)y (43) (1)              (1)              (1)              (1) y41)y  у42)y  у4л  у4л J использованы обозначения

s ; 0 = sh ⁰ a p ’ h k , sh ⁰ a p ⁾ h k = a ¹;^{1 - 1} sh a ;) h « , ⁿ *        ⁿ ) o' ⁿ )h     ^;"          o' ⁿ )h              ^{h n       ( n )}

s pk   ^a p ^{sh a} p ^h k ,  c pk   ^{ch a} p ^h k ,   1 = e , f pk = f pk ,   P , ^k = 1,2,

n ( n ) n *         n *        ( n ) ( n ) ( n ) ( n ) n *        ( n ) ( n ) ( n ) ( n )

¹ pk   ^a k ^l p k ,    4 k    ^U 2332 f 3 k ^{+ U} 2342 f 4 k ,    2kk    ^ 2432 f 3 k ^{+ U} 2442 f 4 k ^{.                (44)}

В случае M = 2 - двухслойное полупространство (см. рис. 1, б) вид матрицы A ^{( 1 )} ( h_M ) определен свойствами слоя, при этом для преднапряженного однородного слоя

' 0 0 1* 11 1* l12 A(1)( hM ) = 0 f311 0 f312 1* 21 0 1* 22 0 ,                                 (45) l Л f412 0 0 J для преднапряженного функционально градиентного слоя A'1 (hM ) = E совпадает с диа гональной единичной матрицей размера 4 х 4.

В случае M >  2 - полупространство со слоистым покрытием матрицы A'^: ( h ₂ M и A принимают вид

0B1(h2) P2(h2)      0 0      B2 (h3) P3 (h3) A1-( h 2.....M )=     0.        0.     B’( h4 ) 0       0       0 l  0       0       0 0 B1 (h)     0        0        0 0       !          0 0       :          0 P4(h4)    :          0 0      :   BM-2 (hM -1)  P 0       :          0i 0            0 0     ^ 0 0 , (46) M-1 (hM -1) ? M-1 (hM) J G1 (h1)) B1(h2) P2(h2) 0         0 0      B2 (h3) P3 (h3)      0 A = 0        0     B3 (h4) P4 (h4) ... 0       0       0       0 V 0        0        0        0 Участвующие в (46) матрицы Bn (hk) и 0            0 0            0 0           0 ... BM-2 (h„-,) PM-1 (h„-1) 0        BM-1 (h„) Pn (hk ) = -Bn ( hk ) определ 0 0 0 . (47) 0 BM (hM L ены свойствами слоев с общей границей hk, имеют размер 4 х 4, верхний индекс отвечает номеру слоя, аргумент – границе раздела (см. рис. 1, а). Для преднапряженного однородного слоя матрица B n (hk) с учетом обозначений (44) определена формулой Bn (hk ) = n*n* l11 51 k n*n* l21 s1k nn f31c1k n*n* l12 s2k n*n* l22 s2k nn f32c2k n*n 11 c1k n*n l21 c1k nn0 f31s1k n*n 12c2k n*n l22c2k nn0 f32s2k ,                         (48) nn nn nn0 nn0 If41 c1 k f42c2k i V f41s1k J 42 5 2 k J для преднапряженного функционально градиентного слоя в n(h )=| КЛ h) L, p=1.                              (49)

Задача II : матрица A имеет размер 4 ( M - 1 ) + 2 , в зависимости от геометрии задачи может быть представлена выражениями (40) и (47). Размер и вид матрицы A ^{( 1 )} ( h ₂ M ) совпадает с соответствующей матрицей задачи I , определяется формулами (45) и (46). Матрицы B ^{( 1 )} ( h 1 ) , B ⁽ M ) ( h_M ) и G ^{( 1 )} ( h 1 ) , участвующие в (40), имеют размер 2 х 4 , 4 х 2 и 2 х 2 . Вид матриц определяется из представлений (41)-(43), путем вычеркивания в выражении G ^{( 1 )} ( h 1 ) 2-й строки и 3-го столбца - матрица становится нулевой, в представлении B ⁽ M ) ( h_M ) 3-го столбца и в представлениях B ^{( 1 )} ( h 1 ) (42), (43) 2-й строки. Размер и вид матриц B n ( h k ) и P ⁿ ( h k ) полностью совпадает с соответствующими матрицами задачи I (48), (49).

• 3.    Определение НДС

В рамках сделанных предположений начально деформированное состояние в каждой из составляющих структуры однородно (1) и может различаться по характеру и величине начальных деформаций. Неоднородность начального напряженного состояния составляющих вызвана только неоднородностью их физических свойств. Характер начального

P ⁽ n ) напряженного состояния определяется тензором Кирхгофа, компоненты которого ^lp

• (15) с учетом свойств материала и предположений об однородности НДС, наведенного за счет механических воздействий в отсутствие внешних начальных электростатических полей определены формулами [6, 7, 12]

р ^{( n} ) _ Д n ) с( n ) . Д ⁿ ) с( ⁿ ) . Дⁿ ) ф ⁿ ) _ 4 ⁿ W^{( n} ) + /7^{( n} )

P 11 c 11 ³ 11 ⁺ c 12 ³ 22 ⁺ c 13 ³ 33 e 31 W 3 ^{+ H} 1 ,

p ^{( n} ) _ J ⁿ ) e( ⁿ ) , J ⁿ ) e( ⁿ ) , J ⁿ ) e( ⁿ ) _ 4 ⁿ W( ⁿ ) , tH ⁿ )

• ¹ 22 ^c 12 ^U11   ^{+ c} 11 ^22 ^{+ c} 13 ^33 e 31 3 ^{+ 21}2 ,

p ^{( n} ) _ J ⁿ ) c^{( n} ) , J ⁿ ) c^{( n} ) , J ⁿ ) c^{( n} ) _ 4 ⁿ )ил^{( n} ) . tr^{( n} )                              /

• ¹33 ^c 13 °11 ^{+ c} 13 °22 ⁺ c 33 °33 e 33 3 +^{1 2}3 ,                         ^(5O)

Д ^{( n} ) _ o^{( n} )rp^{( n} ) z/^{( n} ) - O^{( n})Ш ^{( n} )

1111 , 2112 ,

д ^{( n} ) __p⁽ⁿ )c^{( n} ) .J ⁿ )c^{( n} )      ⁿ )e^{( n} ) ,o^{( n} W^{( n} )

Здесь коэффициенты H ^ ⁿ ) позволяют учитывать влияние модулей упругости III порядка (сумма по немым индексам):

^Hi = c ₅^(:Tqmq q u ^{( v} q ² - ^{1)( v} m ^{2 - 1)} •

В силу предположения об отсутствии начальных внешних электрических воздействий di = 0 и в зависимости от способа задания НДС неизвестными могут быть либо С(n) с(n) е(n) L[/(n) W(n) W(n) иуппымап P(n) V(n) Cn) W(n) W(n) W(n) ЛППРТТРТТаАММР S11 ,S22 ,S33 ,W1 ,W2 ,W3 , либо, например, P11 ,S22 ,S33 ,W1 ,W2 ,W3 , определяемые из решения системы (50). В работе исследовано влияние одноосных НДС: 1 xi ^ Pn) = P, P^ = Pi^ = 0, k, j, i = 1,2,3;

двухосных НДС: 2 xi ^ p iⁿ ) = 0, Р ( " ^ = P kk\jj ^_ti = P , k , j, i = 1,2,3

и гидростатического НДС: 3 x ^ P^_x n ) = P 22 ) = P 3 ( ₃ n ) = P .

Исследования проводились для структур из монокристаллических ZnO [25], CdSe [26] и поликристаллических сегнетоэлектриков, таких как пьезокерамики Soft – PZT DL-61HD, Hard PZT DL-40 [27]. Физические параметры сред приведены в таблице,

8(0) = 8,85^10 12 Ф/м, KS2 = (VF ) -(VF) (VF) - коэффициент электромеханической связи. Относительные скорости волны Гуляева-Блюштейна (ВГБ) для полупространства со свободной и металлизированной поверхностью рассчитаны без учета модулей упругости III порядка.

Физические свойства материалов в ЕС Physical properties of materials in natural state (NS)

	ZnO	CdSe	PZT DL61	PZT DL40
ρ [кг/м3]	5680	5504	8200	7700
с 11 [н/м2]	2,09718·1011	7,4057·1010	14,6000·1010	17,8000·1010
с 12 [н/м2]	1,2114·1011	4,5155·1010	9,6000·1010	10,1000·1010
с 13 [н/м2]	1,0513·1011	3,9302·1010	10,0000·1010	9,2000·1010
с 33 [н/м2]	2,10941·1011	8,3551·1010	13,0000·1010	12,4000·1010
с 44 [н/м2]	4,2449·1010	1,3167·1010	3,9000·1010	2,3000·1010
е 15 [Кл/м2]	–0,59	–0,138	33,10	6,20
е 31 [Кл/м2]	–0,61	–0,159	–15,80	–0,10
е 33 [Кл/м2]	1,14	0,347	25,30	9,00
ε 11 /ε (0)	8,3	9,33	2810,0	290,0
ε 33 /ε(0)	8,8	10,2	2520,0	210,0
V P [м/с]	6097	3668	4219,58	4808
V S [м/с]	2743	1547	2180,85	1728,3
V Se [м/с]	2892	1560	3182,58	2220,8
V GfB / V Se	0,9999417	0,9999986	0,999999982	0,999999082
V GmB / V Se	0,994944441	0,99985181	0,847723696	0,918947544
KS 2	0,01	0,0003	0,28	0,1555

• 4.    Численные результаты

Для детального изучения влияния величины наведенной деформации, вида и характера преднапряжений в составляющих структуры на особенности поведения и скорость распространения поверхностных акустических волн (ПАВ) рассмотрим простейший случай преднапряженного пьезоэлектрического полупространства с преднапряженным однослойным покрытием (M = 2, рис. 1, б). В качестве материала структуры (покрытия и основания) используем гексагональные моно- и поликристаллические сегнетопьезоэлектри- ки (таблица) с различным коэффициентом электромеханической связи, без учета модулей упругости III порядка. Полагаем, что ось симметрии материала в ЕС совпадает с осью x3 , векторы поляризации составляющих покрытия и полупространства совпадают, либо противоположны по направлению (3).

На рис. 2–8 показано влияние характера и величины начальных механических воздействий на относительные фазовые скорости поверхностных волн ( V ^ ¹ / V e 2 ) , где V F = к ₂ / ^ , ^ - решение дисперсионного уравнения (39) с матрицей (40), (47) в зависимости от геометрии задачи в обозначениях (41)–(46), (48)–(49)). Цифрами 0, 1, 2, …, 10 на рисунках отмечено сочетание наведенных деформаций v , ^{( 1 )} / v ^{( 2} - 1/1, 0,97/1, 1,03/1,

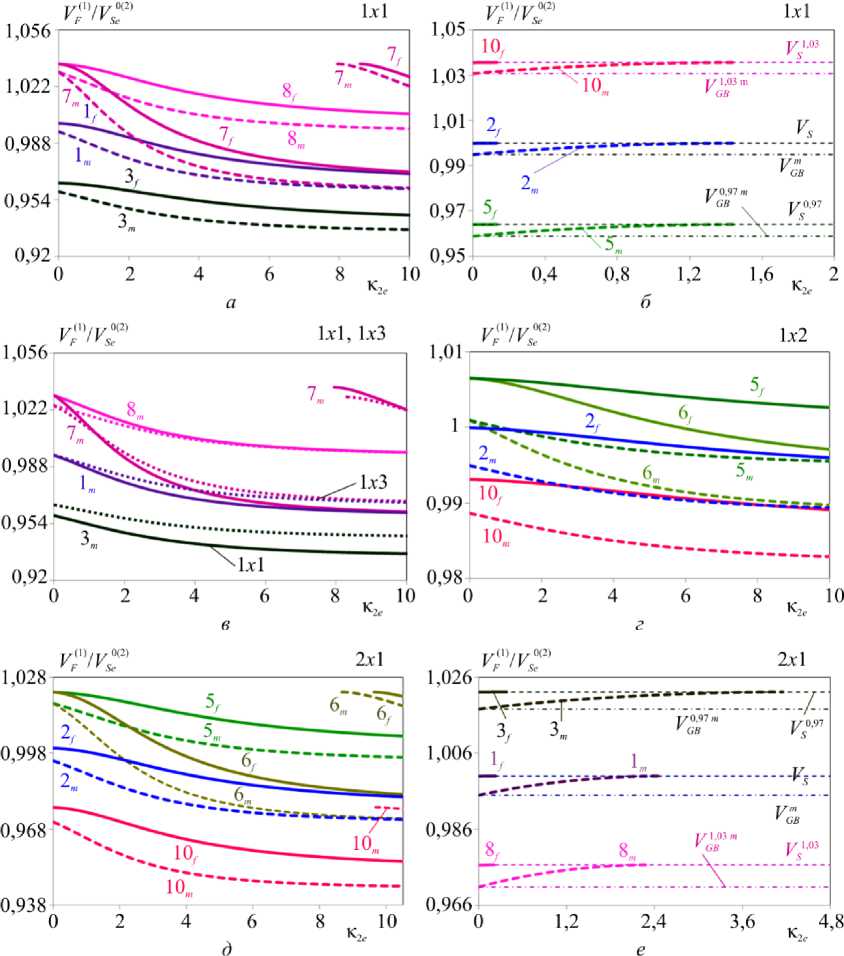
Рис. 2. Влияние величины, характера и типа начальных воздействий на относительные скорости ВГБ для структуры ZnO/ZnO

Fig. 2. Influence of value, nature and type of the initial impacts on relative rates of Bleustein–Gulyaev wave for ZnO / ZnO structure

0,95/0,97, 0,97/0,97, 1/0,97, 1,03/0,97, 0,97/1,03, 1/1,03, 1,03/1,03, 1,06/1,03 соответственно, при этом нижние индексы « f » и « m » обозначают свободную и металлизированную поверхность, верхний индекс « е » случай е ^) = - e 2 .

На рис. 2–4 показано влияние величины и характера начальных напряжений, действующих на составляющие структуры в рамках одного типа НДС, на относительные фазовые скорости ПАВ. Цифрами на рисунках отмечено сочетание деформаций, наведенных действием начальных напряжений в структурах из монокристаллических сегнетоэлектриков ZnO/ZnO (см. рис. 2), CdSe/CdSe (см. рис. 3) и поликристаллических сегнетопьезоке-рамик PZT DL-61/PSZ DL-61, PZT DL-40/PZT DL40 (см. рис.4).

Поляризация в слое и полупространстве совпадает, е ( 5 ) = e 2 ) , сплошными линиями на рисунках обозначены скорости ПАВ задачи I – со свободной поверхностью, штриховыми линиями – задачи II с металлизированной поверхностью. На рис. 2 в , 3 в и 4 а , б показано сравнение влияния одноосных 1 х 1 (сплошные линии) и 1 х 3 (пунктирные линии) начальных напряжений на ПАВ в рассматриваемых структурах с металлизированной поверхностью.

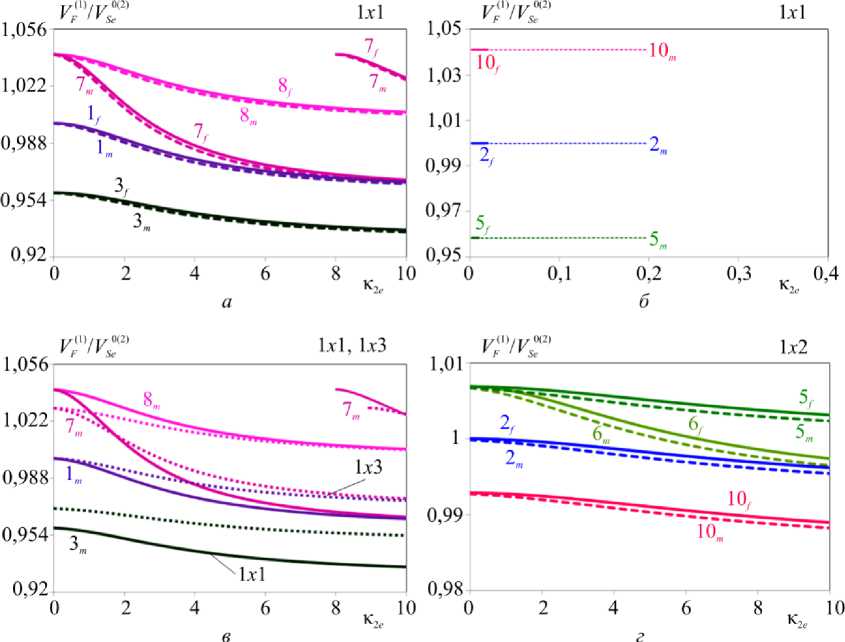
Рис. 3. Влияние величины, характера и типа начальных воздействий на относительные скорости ВГБ для структуры CdSe/CdSe Fig. 3. Influence of value, nature and type of the initial impacts on relative rates of Bleustein–Gulyaev wave for CdSe/CdSe structure

Из сравнения рис. 2 и 3 видно, что при малом значении КЭМС (KS2 ) различие в зависимости фазовых скоростей ПАВ от частоты для задач со свободной и металлизированной поверхностью незначительно (см. рис. 3, а, в). Влияние начальных напряжений, наводящих одноосные НДС в составляющих структуры, минимально в случае 1х2. При 1х1 и 1х3 – влияние соизмеримо и зависит от свойств материала и величины наведенных деформаций. Следует отметить, что воздействие начальных механических напряжений может существенно менять свойства структуры. Так, при определенном соотношении наведенных деформаций (кривые 1, 3, 8 рис. 2, а и 2, 5 рис. 2, г, д) сегнетоэлектрическая структура остается слабо неоднородной: по поверхности распространяется волна Гуляе-ва-Блюштейна (ВГБ), скорость которой в зависимости от характера воздействий может быть больше или меньше значения скорости в ЕС, диапазон изменения незначительный. Соотношение наведенных деформаций 0,97/1,03 при НДС 1х1 (кривые 7 на рис. 2 а, в и рис. 3 а, в) приводит к увеличению диапазона изменения скорости, появляются вторые, а при определенных типах НДС и более высокие моды. Структура перестает быть слабо неоднородной, по поверхности распространяются сдвиговые горизонтально поляризованные волны Лява. Соотношение деформаций 1,03/1, 1/0,97, 1,03/0,97, 1,06/1,03 в рамках

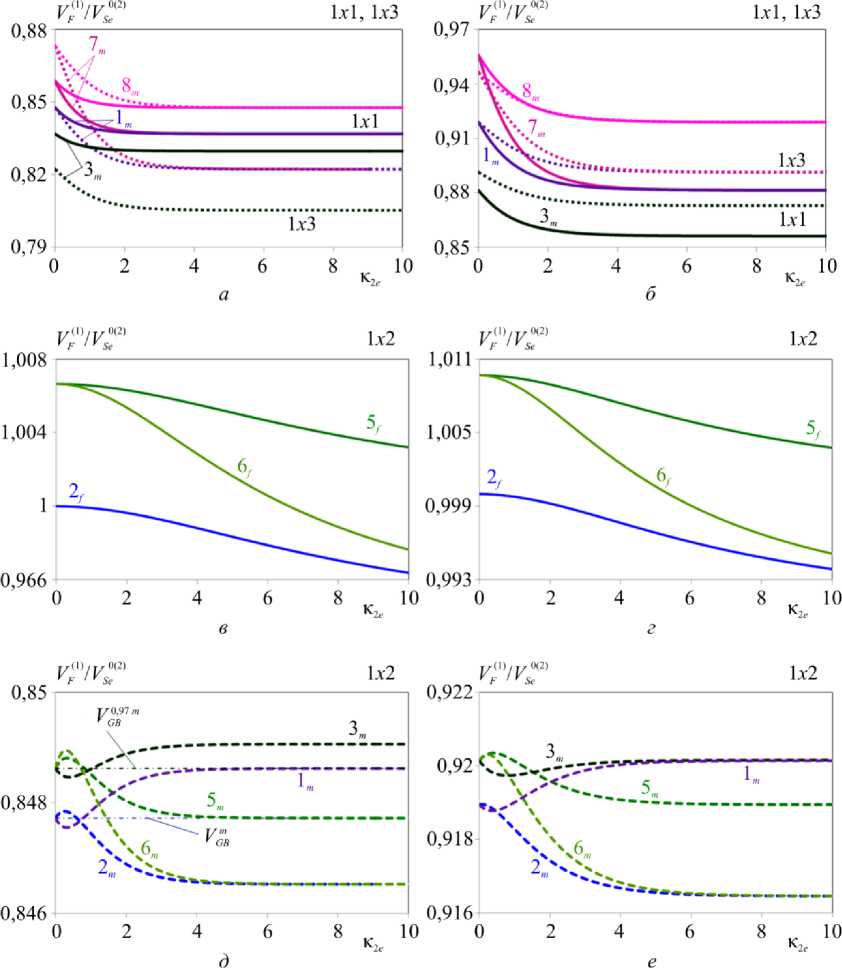
Рис. 4. Влияние НДС на относительные скорости ВГБ для структур PZT DL-61/PZT DL-61 и PZT DL-40/PZT DL-40 Fig. 4. Influence of IDS on relative rates of Bleustein–Gulyaev for PZT DL-61/PZT DL-61 and PZT DL-40/PZT DL-40 structures

НДС 1 х 1 приводит к увеличению скорости ВГБ до значения VS^{а( 2} , волна существует в ограниченном частотном диапазоне, который определяется величиной КЭМС, соотношением деформаций и характером начальных воздействий (см. рис. 2, б , е , рис. 3, б ).

На рис. 4, а – е показано влияние величины, характера и типа наведенных НДС на фазовые скорости ПАВ в структурах из сегнетопьезокерамик PZT DL-61 (см. рис. 4, а , в , д ) и PZT DL-40 (см. рис. 4, б , г , е ) с большим значением КЭМС (таблица). Сравнение одноосных НДС 1 х 1 и 1 х 3 дано на рис. 4, а , б для первых мод ПАВ. В случае структуры из PZT DL-40 в рассматриваемом частотном диапазоне, начиная с к ₂ e = 6,7, появляются вторые моды ПАВ для всех приведенных соотношений деформаций как при НДС 1 х 1, так и при НДС 1 х 3. В случае PZT DL-61 вторые моды в рассматриваемом диапазоне появляются только при НДС 1 х 3.

Из сравнения рис. 2, 3 и 4 видно, что действие начальных напряжений, наводящих в структуре одноосные НДС 1 х 1 или 1 х 3 соизмеримы по влиянию на скорости ПАВ. Для многих пьезоэлектриков преобладающее влияние имеет НДС 1 х 1, однако для ряда сегне-топьезокерамик с высоким значением пьезоэлектрических и диэлектрических модулей в ЕС влияние НДС 1 х 3 может значительно превзойти влияние НДС 1 х 1. Для пьезокерамик с большим значением КЭМС в случае задачи с металлизированной поверхностью характерно существование поверхностной волны во всем частотном диапазоне даже при соотношении наведенных деформаций, приводящих к увеличению фазовой скорости относительно значения скорости ВГБ соответствующего полупространства (рис. 4, д , е ).

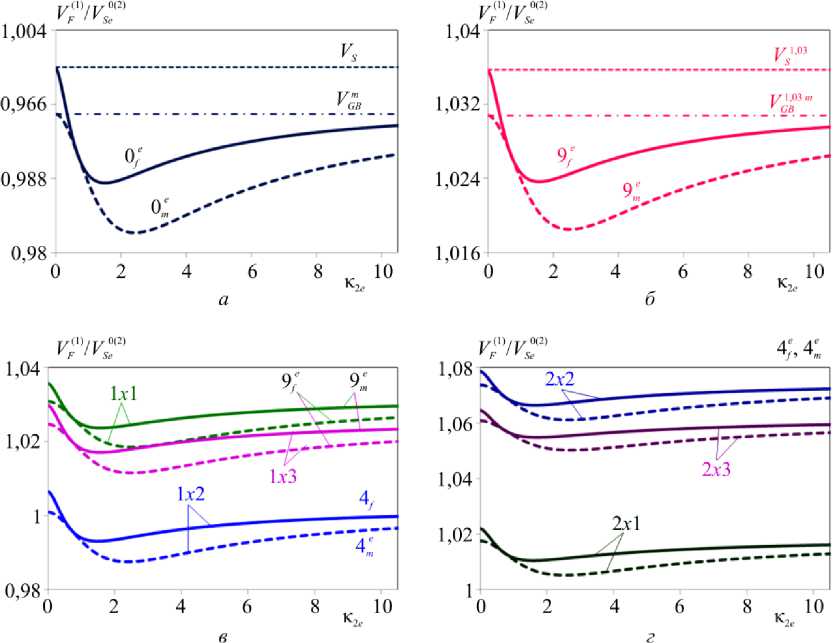
Рис. 5. Влияние величины, характера и типа НДС на относительные скорости ВГБ для структуры ZnO/ZnO

Fig. 5. Influence of value, nature and type of IDS on relative rates of Bleustein–Gulyaev for ZnO/ZnO structure

На рис. 5, а – г показано влияние направления поляризации составляющих структуры ZnO/ZnO (см. рис. 5, а ), величины, характера наведенных деформаций и типа начальных напряжений (см. рис. 5, б – г ) на изменение скорости ВГБ для задач со свободной и металлизированной поверхностью. Предполагается, что наведенные в составляющих структуры деформации равны. На рис. 5, а приведено характерное поведение скорости ВГБ в ЕС ( 1 )         ( 2 )            ( 1 )             ( 2 )

при e y = e i5⁷ и е у =- ^ £5 . В случае НДС 1 х 1 при соотношении наведенных деформаций v 1 ^{( 1 )} / v 1 ⁽ 2 ) = 1,03/1,03 (кривые 9 рис. 5, б ) значение относительных скоростей V GB 0 ³ f IV S⁰^ и V L⁰³ m I V°-² ) достигает значений 1,0356454 и 1,30791675 соответственно.

GB Se

Из рисунков видно, что изменение направления вектора поляризации при всех прочих равных параметрах приводит к изменению характера частотой зависимости скорости ПАВ, среда перестает быть однородной, наблюдается дисперсия свойств (см. рис. 5, а , б ). В рамках действия различных типов НДС в структуре ZnOIZnO при условии e ⁽ 5 ) = - e ⁽ 2 ) наибольшее значение скорости V GB и V B достигают при НДС 1 х 1 (кривые 9 , рис. 5, б , в ) и НДС 2х2 (см. рис. 5, г ).

На рис. 6, а – г и 7, а – г показано влияние на относительные фазовые скорости ПАВ величины и характера начальных напряжений, действующих на составляющие структуры ZnO/ZnO в рамках 1 х 1 (см. рис. 6) и 2 х 1 (см. рис. 7). Рис. а , б иллюстрируют влияние направления вектора поляризации в случае преднапряженного покрытия (рис. а ) и в случае

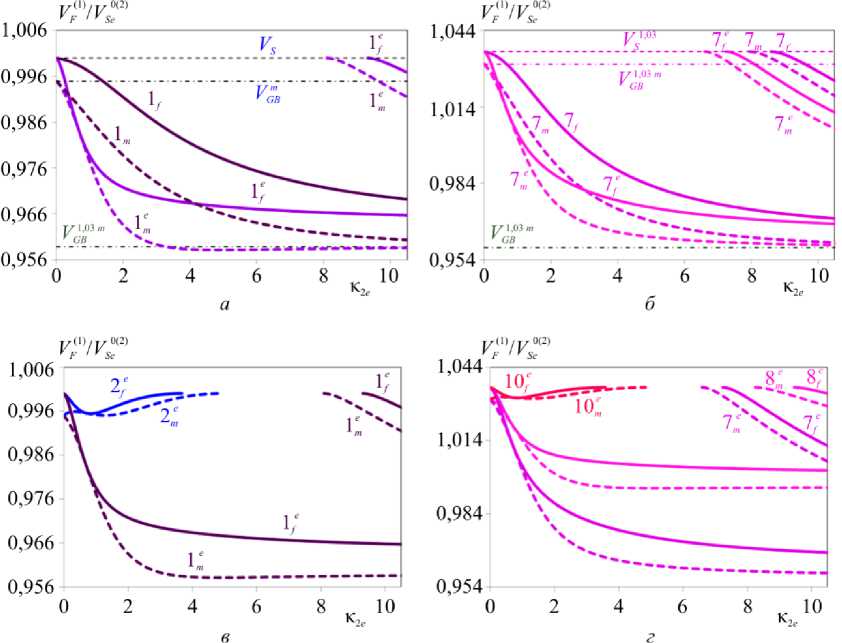
Рис. 6. Влияние на относительные фазовые скорости ПАВ соотношения величины и характера наведенных деформаций в структуре ZnO/ZnO в рамках НДС: 1х1 Fig. 6. Influence on relative phase rates of SAW of relation between value and nature of the induced deformations in structure ZnO/ZnO within IDS: 1х1

преднапряженной структуры (рис. б ). Рис. в , г отражают влияние величины и характера преднапряжений на частотную зависимость фазовых скоростей ПАВ в случае e ( 5 ) = - е ^) .

Цифрами на рисунках отмечено соотношение деформаций, наведенных действием начальных напряжений.

Из сравнения рис. 2, б , е с рис. 6 и 7 видно, что эффекты, вызванные действием различного рода начальных механических напряжений, в пьезоэлектрической структуре существенно зависят от направленности векторов поляризации ее составляющих: в случае е ( 5 ) = - е ⁽ 2 ) относительно е ( 5 ) = е ^) меняется характер частотной зависимости скорости ПАВ, усиливается влияние преднапряжений.

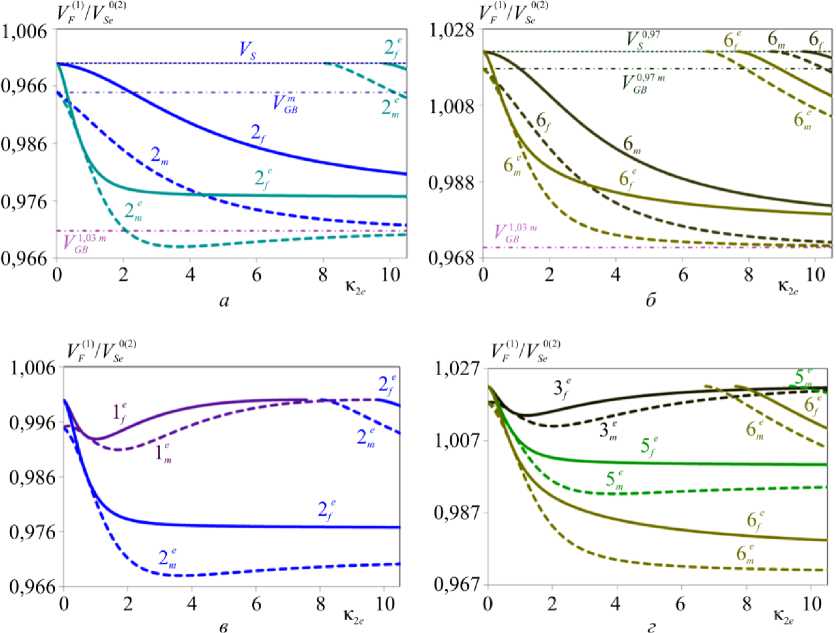
Рис. 7. Влияние на относительные фазовые скорости ПАВ соотношения величины и характера наведенных деформаций в структуре ZnO/ZnO в рамках НДС: 2 х 1 Fig. 7. Influence on relative phase rates of SAW of relation between value and nature of the induced deformations in structure ZnO/ZnO within IDS: 2 х 1

На рис. 8, а , б приведено влияние на фазовые скорости ПАВ начальных напряжений, наводящих в покрытии и основании НДС различных типов. Для удобства сравнения в качестве НДС основания использовано НДС 2 х 2, в качестве НДС покрытия одноосные НДС – 1 х 1, 1 х 2, 1 х 3 (см. рис. 8, а ). На рис. 8, б дано сравнение одноосного 1 х 1 и двухосного 2 х 1 НДС покрытия. Соотношение наведенных деформаций на рис. 8, а , б отвечает случаю 1.03/0.97, векторы поляризации покрытия и основания противоположны по направлению.

Из рис. 8, а , б видно, что при рассматриваемом соотношении деформаций независимо от НДС покрытия в рассматриваемом частотном диапазоне существуют вторые моды ПАВ, минимальное изменение скорости достигается при НДС 1 х 1/2 х 2 (см. рис. 8, а ), максимальное – при НДС 2 х 1/2 х 2 (см. рис. 8, б ). Сравнение рис. 6, а , б с рис. 3 в , г показывает

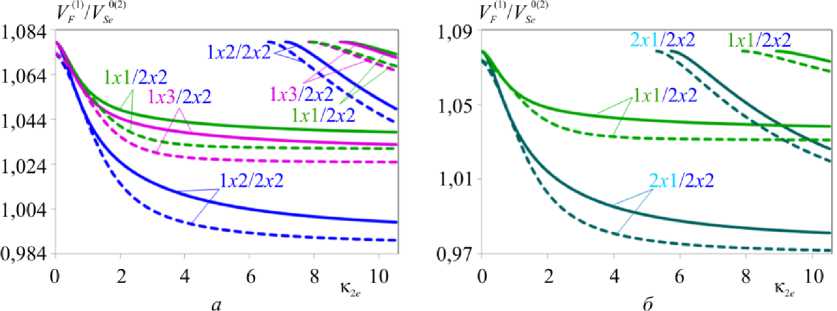
Рис. 8. Влияние типов НДС покрытия и основания на фазовые скорости ПАВ Fig. 8. Influence of IDS types and foundations on SAW phase rates возможность увеличения скорости ПАВ за счет различий в начальных механических воздействиях на составляющие пьезоэлектрической структуры.

Работа выполнена при финансовой поддержке РФФИ (проекты №№15-08-06074, 16-01-00647, 14-08-01213).