Повышение адекватности механико-математической модели динамики ротора на балансировочном станке

Введение. В современной производственной практике приходится решать такие проблемы, как снижение вибрации и шума машин, повышение их надежности и качества функционирования, улучшение условий труда персонала, управляющего работой машины. Эффективным средством решения подобных задач является балансировка роторов — в том числе и высокооборотных карданных передач автомобилей. Этим объясняются высокие требования, предъявляемые к балансировке роторов. В первую очередь речь идет о качестве ее исполнения (на эксплуатационной

Механика

*

∗∗

Работа выполнена по договору № 89-12Н от 27.01.2012.

^∗∗∗ The research is done within the frame of Contract no. 89-12Н, 27.01.2012.

частоте вращения остаточные дисбалансы ротора в плоскостях его коррекции не должны превосходить допустимые значения, регламентируемые технической документацией). Кроме того, следует учитывать трудозатраты балансировки в производстве машин и при их ремонте (минимизация числа балансировочных циклов как основа снижения трудозатрат балансировки).

Реализация этих требований напрямую зависит от адекватности механико-математической модели балансируемого изделия. Использование такой модели на балансировочном станке позволяет установить связь между характеристиками колебаний опор балансируемого изделия и дисбалансами в плоскостях его коррекции с учетом их взаимного влияния на колебания опор.

В первых станках для динамической балансировки роторов (например, станки рамного типа конструкции Б. В. Шитикова [1-3]) задача решалась механическим исключением взаимного влияния плоскостей коррекции. С этой целью последовательно включалась и отключалась податливость шарнирных опор рамы, совмещенных с плоскостями коррекции балансируемого изделия. При этом использовалась простейшая механико-математическая модель балансируемого изделия на станке

Ai = Ki х Di; i = 1,2, (1)

где A = Ai x e ¹⁴¹ ‘ — амплитуда A_t и фаза ф колебания податливой i- й опоры рамы станка при абсолютно жесткой другой ее опоре; К— — скалярный коэффициент влияния, определяемый экспериментально; D— — оценка дисбаланса в i- й плоскости коррекции , сонаправленного с A_— (D _— = D _— x e ^{141 ;} , где D _— — значение, а ф _— — угол дисбаланса D _— ).

Такая модель имеет низкую адекватность и требует большого количества балансировочных циклов, что объясняется необходимостью последовательных замеров и корректировок дисбалансов отдельно в каждой из плоскостей коррекции.

В функционировании появившихся позже станков маятникового типа использовалась модель [4]:

{ A -} =[ K j ]х { D j } ; i = 1,2; j = 1,2,

где {A _—} — матрица-столбец амплитуд и фаз синхронных колебаний опор i = 1, 2 ротора на станке; {D} — матрица-столбец искомых дисбалансов в плоскостях коррекции j = 1, 2 отстоящих от левой и правой опор ротора на расстояния А и С соответственно; [Ку] — матрица скалярных коэффициентов влияния:

[Kj ] = ( l - A - C)-1 х

l - A

C

A l - C

где l — расстояние между опорами ротора на балансировочном станке.

В отличие от (1), модель (2) позволяет получить оценки дисбалансов {D y } сразу в двух плоскостях коррекции за один балансировочный цикл. Однако эти оценки имеют низкую достоверность, т. к. матрица (3) предусматривает статическое распределение дисбалансов между опорами, не учитывая динамические свойства колебательной системы ротора на балансировочном станке. Поэтому, сокращая число балансировочных циклов определения и корректировки {D y }, модель (2), как и модель (1), не имеет достаточно высокой адекватности.

Повышение эффективности функционирования станков маятникового типа привело к необходимости использования механико-математической модели (2) с матрицей скалярных коэффициентов влияния [4, 6-8]:

[ Kij]-

K 11

.^K 21

K 12

^K 22

Элементы которой определяются тарировкой измерительной системы станка на частоте вращения, принятой для балансировки изделия.

Если речь идет об универсальных балансировочных станках, такая матрица строится для заданных совместно диапазонов масс балансировочных изделий и частот их вращения при балансировке.

Модель (2) с матрицей (4) коэффициентов влияния лишь количественно учитывает динамические свойства колебательной системы балансируемого изделия на балансировочном станке. Поэтому дальнейшее повышение адекватности механико-математической модели (2) целесообразно искать с использованием матрицы векторных коэффициентов влияния

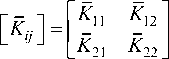
определяемых экспериментально для принятой частоты вращения ротора при его балансировке. Это предложено в работе [9], цитируемой по [10]. Однако на практике данный подход не получил развития из-за отсутствия теоретических обоснований возможности и необходимости его использования, а также из-за сложности его реализации с помощью предложенного в указанных работах графоаналитического метода.

Ниже представлены необходимые теоретические обоснования и практически реализуемая методика определения векторных коэффициентов влияния ^ K i, J ; i = 1, 2; j = 1, 2, обеспечивающих наибольшую адекватность использования механико-математической модели динамики неуравновешенного двухопорного ротора на балансировочном станке:

{A }=[ Ku И D,} ;i=w=(6)

Теоретический анализ коэффициентов влияния. На рис. 1 представлена динамическая модель идеального однородного жесткого двухопорного ротора с податливыми и демпфированными опорами на балансировочном станке.

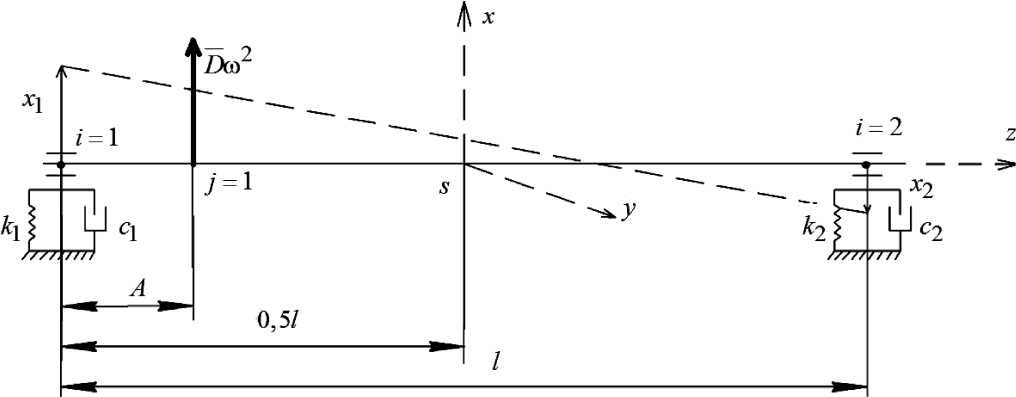
Рис. 1. Модель для анализа колебаний опор ротора на балансировочном станке от проявления дисбаланса D в левой плоскости коррекции ( j' = 1)

Модель имеет две степени свободы, описывающие вынужденные колебания вращающегося со скоростью ω ротора в горизонтальной плоскости xz . Эти колебания генерируются усилием D х го ² от дисбаланса D = D х в^{1 ф D} со значением D. Здесь ф _D — угол идеально уравновешенного ротора, установленного в плоскости коррекции, отстоящей от левой опоры на расстояние А . На рис. 1 показаны положения колебательной системы: статически равновесное (сплошная линия) и текущее (пунктирная линия). Здесь также обозначены: — l — как и ранее, расстояние между опорами ротора;

• —    s — положение центра масс ротора;

— к_г , к 2 — жесткости 1-й и 2-й опор ротора на балансировочном станке;

• —    ^c i , ^сг — коэффициенты диссипативности опор;

  Механика

  
  

• —    х_А , х ₂ — перемещения опор, которые принимаем за обобщенные координаты.

Для составления уравнений движения в обобщенных координатах используем уравнения Лагранжа второго рода с учетом диссипативных сил [11]:

d д Т dt д x

dF д (Т - U

+---(------) = Qi; г = 1,2, дxi      дхг

в которых Т , U — выражения для расчета кинетической и потенциальной энергии; F — диссипативная функция;

Q i — обобщенные силы.

Выражая через обобщенные координаты x1, x2 перемещение х центра S масс ротора и поворот ф его оси как x + x^     x - x^

x = —---- ; Ф = —

2l раскрываем входящие в (7) выражения:

12121                 2I2

T = m х x + I х ф = - m x ( x + x₂ ) + —- x ( x - x^ ) ;

22812 2l212

1   111

U = k x x +   k _? x x ₇ ; F = c x x +   c^ x x₂ ;

2 11 2 22    2 11 2 22

Q 1 = D x m² x ^ x cos ( tot + ф _D ) ;

A

Q2 = D x m x —x cos(mt + фD), в которых m — масса ротора; I — момент инерции ротора относительно оси y.

Выполнив дифференцирование выражений (8) по форме уравнений Лагранжа (7) и используя для решения полученных уравнений метод комплексных амплитуд [11], представляем эти уравнения в матричном виде:

[ A Ы q U B ] x { q } + [ C ] x { q } = { F o } x e^{i m} t ,

где [ A ] =

m +

l m - l

m —

l m +

l

— матрица инерционных коэффициентов; [ B ] = diag [ c 1 c ₂ ] — диагональная матрица

диссипативных коэффициентов; [ C ] = diag [ k 1 k ₂ ] — диагональная матрица квазиупругих коэффициентов;

{Q} = {^i х2}; {Q} = {^ 1 ^2}; (q) = {* 1 х2) — матрицы-столбцы обобщенных ускорений, скоростей и перемещений соответственно; {F0} =  xm x {(l - A) A} — матрица-столбец обобщенных сил.

При решении уравнения (9) в виде {q} = {f }x emt подстановкой входящих в него величин получили выраже- ние для расчета матрицы комплексных амплитуд в виде

(. f } = ( [ C ] — m² x [ A ] + i m x [ B ] )   { F _o } ,

где степень –1 указывает на обращение матрицы, заключенной в круглые скобки.

Раскрывая комплексные амплитуды через их действительные ( a J и мнимые ( b J слагаемые и используя формулу Эйлера, можно записать:

{ f } = { a 1 + ib 1 a₂ + ib₂ } = { A 1 x e ^a 1 A₂ x e ^a 2 } ,                                      (11)

где A = Ja2 + b2 ; a = sign (b-) arccos —i--амплитуда и фаза колебаний i-й опоры ротора на балансировочном стан- i ii iiAi ке (i = 1,2).

Элементы матрицы {/} по (11), определенные по (10), — комплексные величины, т. к. элементы квадратной матрицы

[ L ]^{- 1} = ( [ C ] - m² x [ A ] + i m x [ B ] ) - 1 ,                                           (12)

описывающей собственные свойства колебательной системы ротора на балансировочном станке, являются комплексными числами из-за учета объективно существующего демпфирования в опорных элементах ротора на станке.

Раскрытием входящих в (12) матриц получаем k1 - to2 x

I

[ L r

4 m ₊ _ J + i^{to x} c

— to² x    m — I—

1 4 l ²

— 1

—

2 I 1 I

■ to x m — —

k ₂

2 I 1         I 1 •

— to x m +    + г to x c9

1 4      l ² J         ²

что после обращения матрицы позволяет найти:

где

[ L ] 1

det [ L ]

det [ L ] = < k1 — to2 x

k ₂

—

to² x

I

l ²

I

4 m + _ J + i^{to x} c 2

to ² x| — m — I- 1 4 l²

. . . . I I 7                    2 . .

+ г to x c 1 M k ₂ — to x

2 I 1       I

to x m ——

14      l2.

,        1 I ] I I • k - to x m +    + г to x c

1          1 4 l ² J          1

I

m + -7 4l2

+ i to x c 2

—

,

to4 x| —m — 4;-l4      l2.

— определитель матрицы [L].

Если в рассматриваемой на рис. 1 плоскости коррекции (ее обозначили как j = 1), расположенной на расстоянии А от левой опоры ротора, установлен единичный дисбаланс D, имеющий значение D = 1 и угол ф D = 0, то определенные по (10) комплексные амплитуды будут представлять собой искомые векторные коэффициенты влияния дисбаланса в j = 1-й плоскости коррекции на колебания опор i = 1,2 ротора:

{ K 11 K 21 } = { K 11 x e ^{в 1} 1 K 21 x e ^e 21 } = -l - x [ l ]^{— 1} x { ( l — a ) a } .                                 (15)

На рис. 2 представлена динамическая модель того же, что и на рис. 1, ротора, имеющего те же собственные свойства колебательной системы на балансировочном станке (они описываются той же матрицей [ L ] ¹ по (12)).

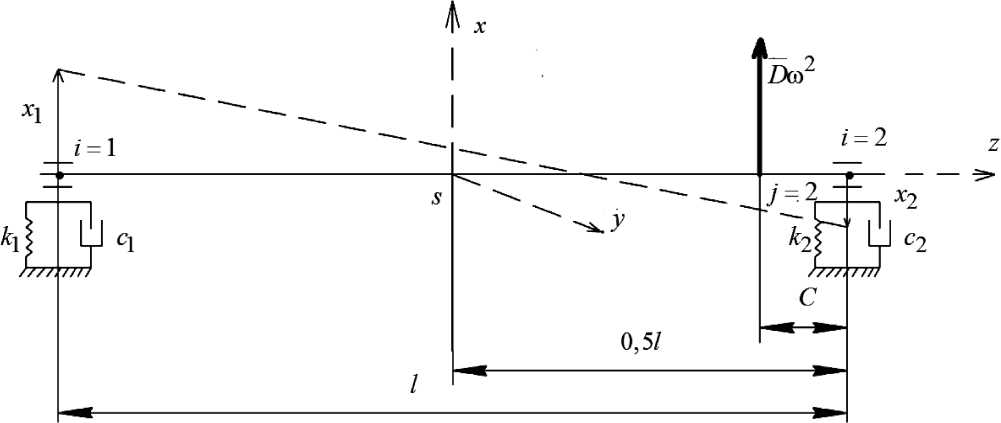
Рис. 2. Модель для анализа колебаний опор ротора на балансировочном станке от проявления дисбаланса D в правой плоскости коррекции (j' = 2)

Колебания опор этого идеально уравновешенного ротора при его вращении на балансировочном станке возбуждаются лишь дисбалансом D, установленным в плоскости коррекции j = 2, расположенной на расстоянии С от правой опоры i = 2 ротора.

Колебательный процесс модели на рис. 2 будет описываться тем же уравнением (9), в котором матрица – столбец обобщенных сил должна представляться как

{ F o } = D ^ to L _Х{ _С ( l — C ) } .                                         (16)

Принимая D = 1, φ D = 0 и подставляя (16) в (10), получаем уравнения для расчета коэффициентов влияния дисбаланса в плоскости коррекции j = 2 на колебания опор i = 1,2 ротора на балансировочном станке:

Механика

__ 2

{ K 12 K 22 } = { K 12 х e^ K 22 х e i ^e 2 ² } = — х [ L ]^{- 1} х { С ( l - С ) } ,

в котором [ L ] ^{- 1} та же, что и в (15).

Анализ теоретических зависимостей (15), (17) и входящих в них соотношений (13), (14) позволяет утверждать следующее:

• —    учитывая наличие демпфирования колебаний опор ротора на балансировочном станке, коэффициенты влияния дисбалансов в плоскостях коррекции j = 1,2 на колебания опор i = 1,2 ротора необходимо рассматривать как векторные величины ( K ij = K ij х e ^e j , i = 1,2 ; j = 1,2 );

• —    значения K j и углы P j коэффициентов влияния K j существенно зависят от скорости w балансировки ротора на станке. От — зависят также характеристики { A i } колебаний опор неуравновешенного ротора на балансировочном станке. Поэтому для использования модели (6) при балансировке ротора элементы матриц { A i } и ^ K ij J должны быть определены на одной и той же скорости го вращения ротора. При этом значение го балансировки жесткого ротора не влияет на определяемые посредством (6) характеристики { D j } его неуравновешенности;

• —    векторы K j практически не совпадают как по значениям, так и по углам для любых сочетаний i и j. Лишь теорети

чески не исключен случай, когда k 1 = k ₂ , c 1 = c ₂ , A = С , при котором имеет место K_n = K ₂₂ ; K ₁₂ = K ₂₁ ;

• —    значения и углы векторных коэффициентов влияния для принятой скорости го балансировки заданной конструкции ротора на определенном балансировочном станке зависят только от координаты, определяющей положение плоскости коррекции относительно одной из опор ротора.

Поясняя последнее, отметим, что при подстановке в (15) задаваемого значения А, определяющего положение плоскости коррекции j = 1 относительно опоры i = 1, рассчитывается матрица-столбец {K11 K21} коэффициентов влияния. Если в том же уравнении (15) принять А = I — С — координату плоскости коррекции j = 2 относительно i = 1 -й опоры, то результатом расчета будет матрица-столбец {K12K22} коэффициентов влияния. Те же результаты получаются и с использованием уравнения (17). В этом случае в расчет вводятся значения С — расстояния от плоскости коррекции j = 2 до опоры i = 2 ротора на станке, и таким образом находится матрица-столбец {K12 K22} коэффициентов влияния. Принимая в том же уравнении С = l - A — расстояние от опоры i = 2 до плоскости коррекции j = 1, нахо дим матрицу-столбец {K11K21} коэффициентов влияния.

Таким образом, по каждому из соотношений (15), (17) могут быть найдены коэффициенты влияния дисбаланса в любой плоскости коррекции (не только в j = 1, 2) на колебания опор i = 1, 2 ротора на балансировочном станке. Для этого задается либо расстояние А (рис. 1 с использованием уравнения (15)), либо расстояние С (рис. 2 с использованием уравнения (17)).

Методика определения коэффициентов влияния. При балансировке конкретного изделия находить векторные коэффициенты влияния аналитическим методом нерационально из-за трудоемкости и неточности определения величин, входящих в (15) или (17), и, как следствие, значительной погрешности результатов расчета. Аналогичным образом объясняется отказ от использования векторных коэффициентов влияния с графическим методом их определения [9, 10], о чем упоминалось выше.

Излагаемая ниже методика натурного определения векторных коэффициентов влияния для жесткого двухопорного ротора строится на ряде допущений.

• —    Амплитуды Ai , фазы a i колебаний A i = A i х e i ^а ‘ опор i = 1, 2 ротора и частота его вращения при балансировке

определяются только характеристиками неуравновешенности ротора.

— Неуравновешенность ротора полностью определяется искомыми и корректируемыми при балансировке дисбалансами D j = D j х e ^ф j в двух заданных плоскостях его коррекции ( j' = 1,2).

• —    При анализе малых колебаний опор ротора от различных источников используется принцип суперпозиции. Возможность принятия этих допущений при моделировании неуравновешенности и колебаний жестких роторов на балансировочном станке доказана существующей практикой балансировки.

  Рассмотрим ротор, имеющий в заданных плоскостях коррекции j = 1, 2 искомые дисбалансы   D 1 = D 1 х ё ^{Ф 1} ,

  D 2 = D 2 х ё ^Ф 2 . C приведением этого ротора во вращение на балансировочном станке колебания A его опор будут описываться выражением (6), раскрываемом как

  A = K 11 х D 1 + K ₁₂ х D ₂ ;

  
  

  A 2 = ^K 21 ^х D 1 ^{+ K} 22 ^х D 2 .

  
  
  
  

  Установим в плоскости коррекции j = 1 пробный дисбаланс D_n 1 = D_n 1 х ё ^Ф п ¹ с заданными значением D _n 1 и уг-

  
  

  лом φ_П 1 . После приведения во вращение колебания опор этого ротора будут описываться:

  A 1 = K ; х ( D + D ; ) + K 2 х D; ;

  
  

  A 21 = K 21 х ( D 1 + Dm ) + K 22 х D 2 .

  
  
  
  

  Вычитая из (19) выражения (18), находим

  
  

  A 11 - A 1 = A 1 х ё ^а 11 - A 1 х ё ^а 1 = K 11 х D _{n 1} х ё^ф п ¹ ;

  A 21 - A 2 = A 21 х ё ”²¹ - A 2 х e^{l a} 2 = K 21 х Dm х ё^ф п ¹ .

  
  

  Отсюда

  
  

  K _H = K _H х ё»¹

  
  

  A 11 х ё ^а» - A х ё ^а D _n 1 х ё^ф - ¹

  
  

  K 21 = K ₂₁ х ё ^в 2>

  
  

  A ₂₁ х ё^{1 а} 21 - A ₂ х ё ^а

  D _{n 1} х ё ^Ф п ¹

  
  
  
  

  Удалим из плоскости коррекции j = 1 дисбаланс D _п 1 и установим в плоскости коррекции j = 2 пробный дисбаланс

  D_{n 2} = D_{n 2} х ё^{1 Ф п 2} с заданными значением D_{n 2} и углом ф_ш. Опишем колебания опор этого ротора на станке:

  A 1; = K U х D 1 + K 12 х ( D 2 + D - 2 ) ;

  
  

  A 22 = K 21 х D 1 + K 22 х ( D 2 + D _n 2 )

  
  
  
  

  Вычитая из (21) уравнения (18), окончательно получаем:

  K 12 = K 12 х ё^{1 в} >² :

  K ₂₂ = K ₂₂ х ё^ ²² :

  
  

  A ₁₂ х ё ^a 1 ² - A ! х ё ^а 1 .

  D _{n 2} х ё^ф - 2      ’

  A ₂₂ х ё ^а 2 ² - A ₂ х ё“²

  D _{n 2} х ё ^Ф п ²

  
  
  
  

  Выражения (20), (22) определяют векторные коэффициенты влияния через заданные характеристики пробных дисбалансов D _п 1 , D _п 2 и определенные замерами на балансировочном станке характеристики (амплитуды и фазы) колебаний опор = 1, 2 ротора с пробными дисбалансами и без них.

  Формируя по результатам расчетов матрицу ^ K j J по (5), находим дисбалансы D 1 , D ₂ балансируемого ротора в при-

  
  

  нятых плоскостях его коррекции:

  
  

  { D i } =[ ^Kj Г х { A l } .

  
  
  
  

  При необходимости балансировки партии изделий одного типоразмера (как это требуется, например, при балансировке карданных передач в производстве и ремонте автомобилей одной модели) матрица [Ку], построенная по изложенной методике для одного изделия, «обучает» измерительную систему станка для использования ее при балансировке всех изделий партии.

  В лаборатории «Динамика приводов, вибрации и диагностика качества машин» Донского государственного технического университета был поставлен эксперимент. В ходе работы была реализована балансировка двухшарнирной карданной передачи 2121-2201012-04 автомобиля «Нива» по существующей технологии с использованием матри-

  
  

  Механика

  
  

цы скалярных коэффициентов влияния (4) и балансировка той же передачи по новой технологии с использованием матрицы векторных коэффициентов влияния (5). С учетом контрольного измерения первая технология была реализована за 5 балансировочных циклов, вторая — за два цикла при одних и тех же значениях допустимых дисбалансов.

Заключение. Для разработки балансировочного оборудования нового поколения и прогрессивных технологий балансировки следует использовать механико-математические модели. В данном случае речь идет о моделях динамики ротора с векторными коэффициентами влияния дисбалансов в плоскостях коррекции на характеристики колебаний опор. Целесообразность такого подхода теоретически обоснована. Предложенная методика определения векторных коэффициентов влияния обеспечивает получение достоверных результатов и легко реализуется на компьютере. Обеспечивая более высокую адекватность, модель с векторными коэффициентами влияния позволяет повысить точность определения дисбалансов балансируемого изделия в плоскостях коррекции, уменьшая тем самым необходимое число балансировочных циклов и трудозатраты балансировки.