Повышение дальности радиорелейного интервала путем компенсации влияния распределенных параметров антенной опоры

R ^~U + B—+ Ku = f, d 2 d t J (1)

где u – вектор обобщенных смещений; R – матрица инерционных характеристик или удельная масса; B = T + DC i D - оператор рассеивания энергии; K = DCD - оператор теории упругости; f – вектор-функция внешних нагрузок; C и C₁ – соответственно матрицы или тензоры упругих постоянных и коэффициентов внутреннего трения.

Граничные условия:

n^C + C1 T^ u = fs на Si;

u = 0 на S2 .                            (2)

Начальные условия:

^u\_t = ₀ = a o^;

d u

d t

= a i . t = 0

Уравнение колебаний стержней с учетом сжимающих сил преобразуется по Лапласу при ненулевых начальных условиях [2]. Затем составляются уравнения равновесия узлов, которые представляют собой систему уравнений для неизвестных узловых перемещений, то есть соответствующих уравнений метода конечных элементов (МКЭ). Разрешающие уравнения в матричном виде для n -го узла записываются следующим образом:

BnpU p

+ Ans

BnrUr + (Anp

+ Anr

+

2,

+ Ant + Cn to In)Un  BnsUs

- B nt U t ...

...   ^Bnp

U p

^Bnr [Ur ]

- Bns [ Us ] - Bnt [U_t ] + Rn ;          (4)

Рис. 1. Допустимый угол отклонения опоры с антенной RFS ПИ,2м

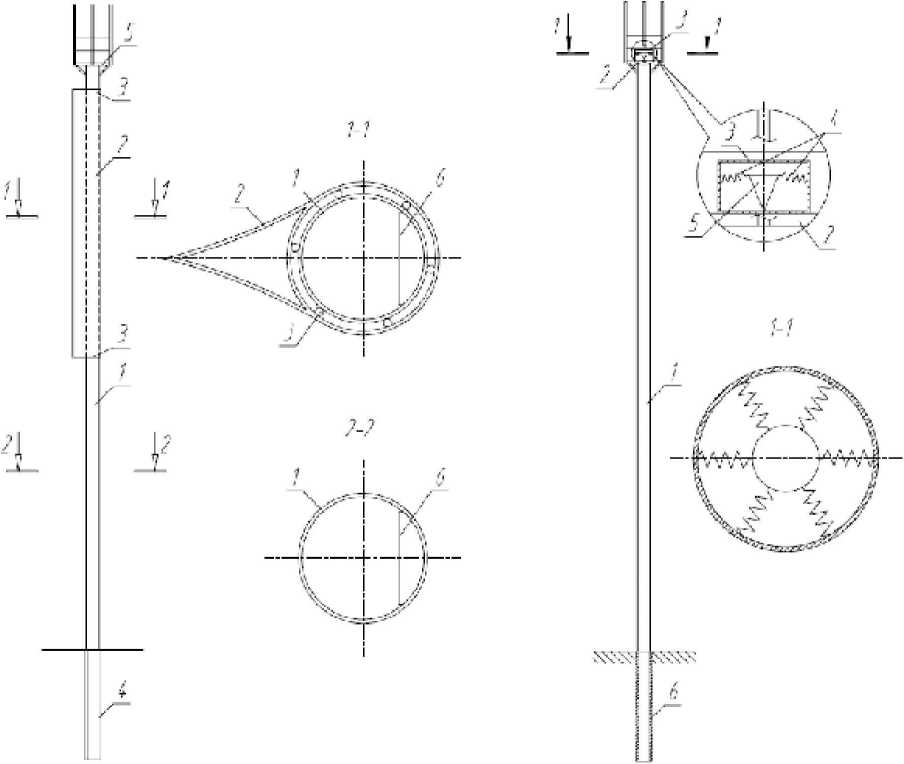
Рис. 3. Антенная опора с динамическим гасителем

Рис. 2. Антенная опора с каплевидным кожухом

Aik и Aik^ ’ ^nk и Aikn

(п0 О Л           Г л П

»= л ;М = "  «к ;

О и о)L J тОО  О   0о

О т О  О    ОО

О 0 т  О    ОО

ООО J х ^ ху "Jxz

ООО ~J ух J у —Jyz ООО "Ах~Av А cx o o 0 о о О cy 0 0 0 0

О о cz 0 о о

О о о cy 0 0

ООО о cy 0 0000 о cy

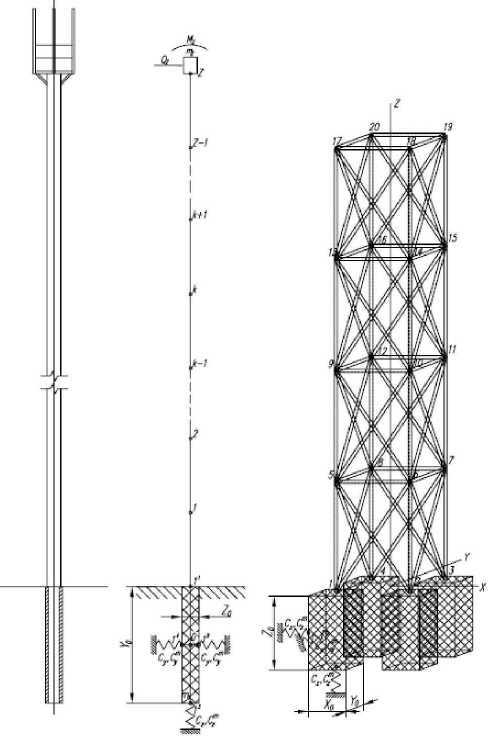
Рис. 4. Расчетная схема антенной опоры в виде стержня где ng ^ матрица направляющих косинусов; Ап к ’ Впк - матрицы динамических жесткостей стержня в местной системе координат, совпадающей с его главными центральными осями; [ О к ] ^ вектор перемещений конца стержня от местной нагрузки. Элементы матриц А®,- , В®к и Ш f I определяются по формулам, приведен-

s„k о   о  о   о0

о

G^ 0  0  0c^

Лк-

О ^ynk 0 ~^ ynk 0 0 0^0 0’

^ -Cynk 0 ^ynk^

^ znk 0^0 Ank

Tnk 0 о о о 0 о H 1  0 о 0 -D , v zm       u         znk n 0  0 Hynk 0 Dynk 0

ВиО =

0 0 о Fnk О 0 о 0 -D^ О -B^ 0 ^ ^znk О 0   0 ~^znk

^ =|к]-Ы-Ы-[4],ШМ1|

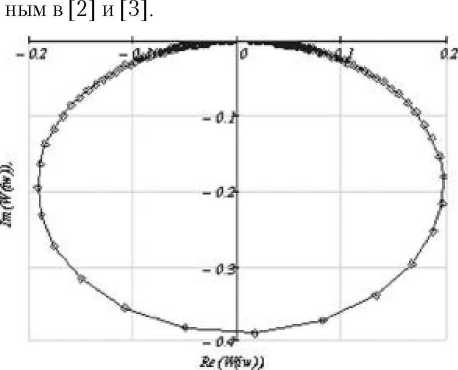
Рис. 5. АФЧХ стержневой системы по углу отклонения

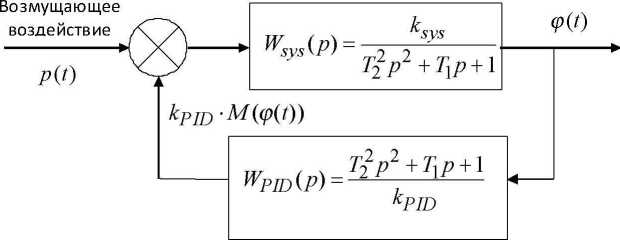
Рис. 6. Структурная схема системы управления

Решая полученные уравнения при р = / • (О, где Р - параметр преобразования Лапласа, со - частотный параметр, строятся амплитудно-фазо-частотные характеристики (АФЧХ) стержневой системы.

АФЧХ антенной опоры в виде стержня (рис.4) представлена на рис. 5.

Как видно из рис. 5, АФЧХ имеет один ярко выраженный доминирующий виток, что показывает, что система ведет себя как система с одной степенью свободы. Таким образом, оказывается возможным эффективно использовать систему управления, структурная схема которой показана на рис.6. Ее передаточная функция определяется по формуле [4], [5]:

• ¹    + ^у® • ^WPID

где WPID (р) =         ----, kPID " ksys

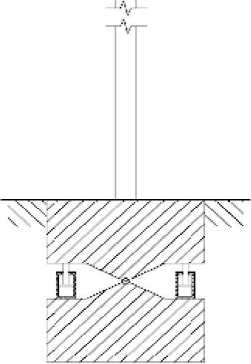
Рис. 7. расчетная схема антенной опоры с активным гасителем

__________0.12_________0.017р2 + 0.003973/7 + 1 ' (7)

Конструктивное исполнение антенной опоры с активным гасителем в виде гидроопор показано на рис. 7, на рис. 8 приведена АФЧХ системы.

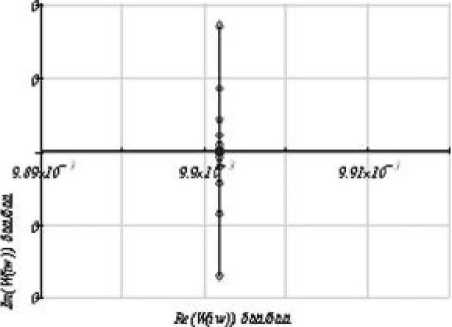
Рис. 8. АФЧХ стержневой системы с активным гасителем по углу отклонения

л» IJ¹ A /./ ■ I;

-or

t.c

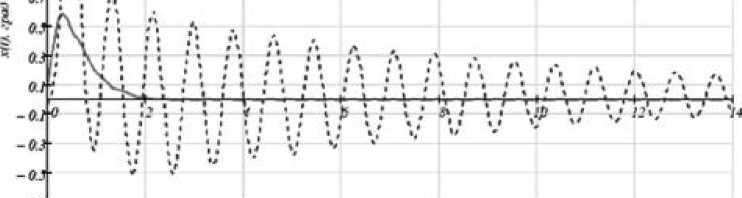
Рис. 9. Переходные процессы по углу отклонения

Принимая k_PID = 100 строим переходный процесс по углу отклонения радиолуча (рис. 9, сплошная линия), пунктирной линией показан переходный процесс антенной опоры без гасителя.

Выводы:

Получена компактная математическая модель антенной опоры, являющаяся результатом обработки решения нескольких десятков уравнений.

На основании динамической модели антенной опоры предложено активное устройство для снижения амплитуды колебаний при ветровых возмущениях.

Применение активного гасителя теоретически позволяет почти полностью исключить угол отклонения радиолуча излучающей антенны (типа “узкий луч”) и увеличить радиус уверенного приема, когда ограничением зоны уверенного приема является линия горизонта.