Повышение долговечности элементов теплоэнергетического оборудования на основе моделирования разнотолщинности стенок труб в процессе гиба

Точная математическая модель изгиба трубы представляет собой сложную трехмерную задачу аналитического определения разно-толщинности полой цилиндрической конструкции после ее изгиба и трансформации в тороидальную форму.

Принципиальная схема петли трубы пароперегревателя с изгибом малого диаметра представлена на рисунке 1. Этот рисунок отображает тот факт, что начальный цилиндрический отрезок трубы длиной «2L» (рис. 6) с одинаковой толщиной стенки «Т» при изгибе по радиусу «г» матрицы трансформирует свое первоначальное сечение Ац и Вц с центром в точке Оц в сечение А и В с центром в точке О. Схема перераспределения толщины стенки трубы вдоль параллелей иллюстрируется рисунком 2. На рисунке 3 приведена расчетная схема объема элементарного куба (1-2-3-4-5-6-7-8), вырезанного из тороидальной части стенки изогнутой трубы пароперегревателя. На рисунках 4 и 5 приведены схемы расчета усредненной толщины стенки трубы по кольцевым меридиональным сечениям «А» и «В», то есть в зависимости от угла φ. Рисунок 3.6 иллюстрирует схему расчета усредненной толщины стенки трубы по длине параллелей, с учетом предварительно усредненных значений по кольцевым меридиональным сечениям «А» и «В»

Осевое сечение тора (меридиан) распадается на две окружности.

Нормальное к оси сечение тора (параллели) распадается на две концентрические окружности.

d – диаметр трубы пароперегревателя;

r – минимальный радиус внутренней части изгиба трубы (матрицы гиба);

R – максимальный радиус внешней (наружной) части изгиба трубы;

T – исходная толщина стенки трубы пароперегревателя;

t – величина утолщения внутренней и утонения наружной стенки трубы;

γ – угол наклона меридионального сечения к оси симметрии змеевика;

φ – угол наклона радиуса кривизны кругового меридионального сечения к оси его симметрии;

d γ – дифференциал угла γ;

(T + t) – увеличившаяся толщина стенки внутренней части гиба трубы;

(T – t) – уменьшившаяся толщина стенки наружной части гиба трубы.

Криволинейный четырехугольник 1-2-3-4 представляет собой след на поверхности тора от вырезанного из стенки изогнутой трубы элементарного куба (1-2-3-4-5-6-7-8), изображенного на рисунке 3.

r с – радиус кривизны к параллели внешней поверхности тороидальной части изогнутой трубы (Рис.3);

d φ –дифференциал угла φ (Рис.3);

Т(γ, φ) –переменная толщина стенки изогнутой части трубы, являющаяся функцией двух переменных γ и φ.

Точка «М» является центром кривизны изгибаемой тороидальной части трубы, точка «О» представляет собой центр кривизны кругового меридионального сечения тороидальной части гиба.

Для приближенного аналитического решения задачи и оценки разнотолщинности стенок изгибаемой части трубы будем рассматривать одну из ее симметричных половин (в данном случае верхнее полупространство). В связи с симметрией этой рассматриваемой части относительно оси Д-Д, делящей поперечное сечение трубы пополам, будем составлять математическую модель перераспределения толщины стенки между объемами материала трубы с проекциями сечений А и В на плоскость переднего полупространства, как это изображено на рисунках 1 и 2.

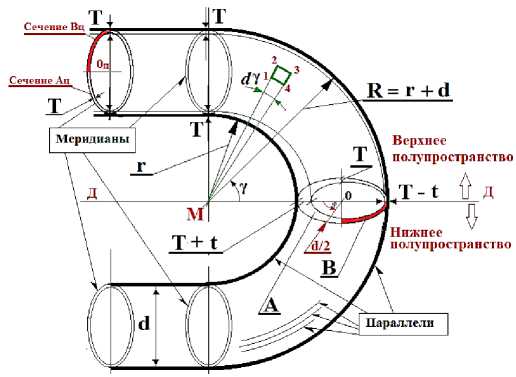
Рисунок 1 – Схема петли трубы пароперегревателя с изгибом малого диаметра

Минимальный радиус гиба выбран из технологических соображений и составляет:

• -    при нагреве набитой песком детали – r = 3.0 d;

• -    на трубогибочном станке (изгибание холодным способом) – r = 3,5 d;

• -    с получением рифленых складок (гнутье горячим способом) – r = 2.0 d.

  

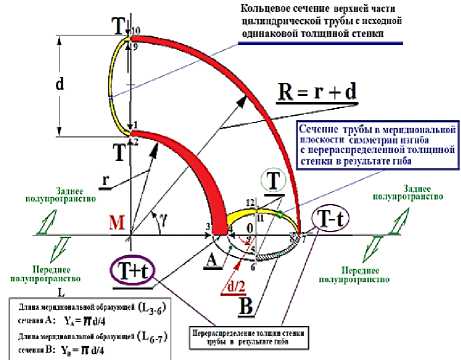
  Рисунок 2 – Схема перераспределения толщины стенки трубы между объемами материала (выделено красным цветом) , расположенными в переднем верхнем полупростанстве с сечениями А и В в нижней части эллипса

  
  
  

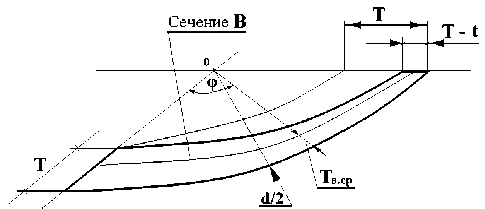
  Рисунок 5 – Схема расчета усредненной толщины стенки трубы по кольцевому меридиональному сечению «В» трубы пароперегревателя

  
  
  

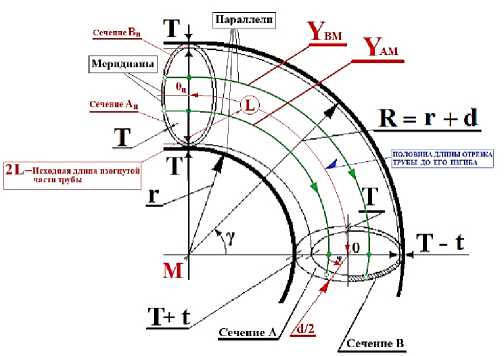
  Рисунок 6 – Схема расчета усредненной толщины стенки трубы по длине параллелей, с учетом усредненных значений толщин по кольцевым меридиональным сечениям «А» и «В»

  
  
  

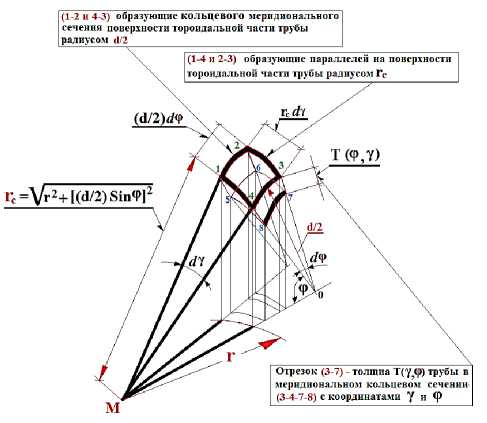
  Рисунок 3 – Расчетная схема объема элементарного куба (1-2-3-4-5-6-7-8) , вырезанного из тороидальной части стенки трубы

  
  

  Т + t

  
  
  

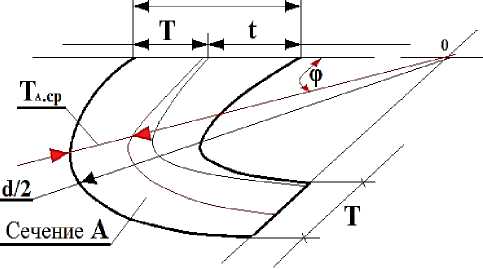
  Рисунок 4 – Схема расчета усредненной толщины стенки трубы по кольцевому меридиональному сечению «А» трубы пароперегревателя

  
  

После построения физической модели процесса перераспределения толщины стенки трубы при ее гибе переходим к математическому описанию этого процесса.

Для аналитического определения закона перераспределения между сечениями А и В толщины стенки Т (рисунки 1., 2., 6.) цилиндрической трубы диаметром d, воспользуемся условием сплошности (неразрывности), то есть равенства до и после изгиба по радиусу «r» вырезанного из изогнутой части трубы объема V А с сечением 3-4-5-6 (сечение А) в меридиональной плоскости и с сечением 1-23-4 в плоскости параллели внутреннего обода, а также объема V В с сечением 5-6-7-8 (сечение В) в меридиональной плоскости симметрии изгиба трубы и сечением 7-8-9-10 в плоскости параллели внешнего обода.

Примем основные допущения, позволяющие рассматривать задачу как чисто стереометрическую: 1) будем учитывать перемещение объемов материала стенки трубы в направлении параллелей, без учета перемещения объемов материала стенки в направлении меридианов, 2) возможной анизо-       Здесь величина (d/2ф) Sinф представляет со- тропии материала стенки трубы пренебрегаем. бой координату центра тяжести кольцевого сектора

Такие допущения значительно упрощаютс углом полураствора «φ» меридионального сече-решения трехмерной задачи изменения толщиныния (Рис. 4, 5.).

стенки трубы методами теории упругости, приве-      После определения средних объемных зна- денные в работах Мальцева Д.Н. [17], Михайловачений толщины стенки ТАсри Твср,   определяем

В.Н. [19], Козлова А.В., Шеркунова В.Г. [14] и дру-среднеобъемное значение площадей меридиональ-гих исследователей.                           ных сечений

В условиях принятых допущений очевидно, S a и S b по соотношениям:

что толщина стенки является функцией двух переменных: ф и у, уменьшаясь от (Т + 1) до (Т -1) при увеличении φ от 0 до 180о. При изменении γ от 0 до

S a = Т Аср • Y a , S b = Т вср • Y b .

Воспользуемся теперь второй теоремой

90о, толщина стенки уменьшается от (Т +1) до Т поПаппа-Гульдина: Объем тела, полученного от вра-параллели радиуса «г» (внутренний обод гиба) ищения плоской фигуры вокруг непересекающей ее возрастает от (Т -1) до Т по параллели радиуса «К»оси, равен произведению площади этой фигуры на

(наружный обод гиба).

Определим для вырезанного из изогнутойфигуры [11].

длину окружности, описаной центром тяжести этой

части трубы материала объем V a с сечением 3-4-5-

Таким образом, для объемов материалов

6 (сечение А) в меридиональной плоскости и с се-трубы с сечениями А и В можем записать очевид-чением 1-2-3-4 в плоскости параллели внутреннегоные соотношения:

обода, а также объем V b с сечением 5-6-7-8 (сечение В) в меридиональной плоскости симметрии изгиба трубы и сечением 7-8-9-10 в плоскости парал-

V a — S a • Y am = Т Аср • Y a • Y am .

V b — S b • Y bm = Т вср • Y b • Y am .

Тогда уравнение неразрывности (сплош-

лели внешнего обода исходя и стереометрическихности) для удвоенных объемов V a и V b прини-

соображений, пользуясь рисунками 2 - 6.

Для сечения А (рис. 4.), при равномерном изменении толщины стенки Т трубы по линейному

мает вид:

2V a —2V b , или

2 Т Аср • Y a • Y am . = 2Т вср • Y b • Y bm .

закону в зависимости от изменения угла поворотаПосле раскрытия обозначений через «1», «d», др радиуса меридионального поперечного сечения«Т» и «г», получим соотношение:

(3-4-5-6), ее средняя величина Т Аср.п составит значение:

Т Аср.п = [(Т +1) + T]/2 = T +1/2.

(T + 1/4>nd/4 ^ п{г + d/2[1-(Sin ф)/ф)]} — (T - 1/4>nd/4 ^ п{г + d/2[1+(Sin ф)/ф)]}

Для сечений А и В значение ф составляет

Учитывая меридиональное изменение тол-п/2, поэтому получим следующее уравнение для щины стенки Т трубы от изменения угла поворотаопределения величины утонения «1» исходной dY самого сечения при гибе, определим объемнуютолщины трубы «Т»:

среднюю величину Т Аср по соотношению: (T +1/4) • nd/4 • п[г + d/2(1-2/ п)] = (T - 1/4) • ndM ^

Т Аср = (Т Аср.п + T)/2 = [(Т +1/2) +T]/2 — T +I 4. п[г + d/2(1+2/n)].

Аналогично для сечения В (рис. 3.5.), при После несложных алгебраических пре-равномерном изменении толщины стенки Т трубыобразований получим стереометрическую мате-по линейному закону в зависимости от измененияматическую модель перераспределения тол-угла поворота др радиуса меридионального попе-щины изгибаемой цилиндрической трубы по ме-речного сечения (5-6-7-8), ее средняя величинаридиональному сечению в виде:

Т вср.п составит значение:

Т вср.п = [(Т -1) + T]/2 — T -1/2.

Т вср = (Т вср.п + T)/2 = [(Т -1/2) +T]/2 — T - 1/4.

1 = (4/п) _т, ¹  ,  .

V ’ r/d + l/2

Анализируя полученное уравнение, за-

Длины Y a и Y b внешних меридиональных^{мечаем вполне} логичную закономерность уве^-образующих сечения А и сечения В (рис. 2.) пред-^{личения степени} утонения толщины «¹» стенки ставляют собой четверти окружности с диаметром^{цилиндрической изгибаемой трубы с увеличе-}_{d и составляют величину:}                      нием ее первоначальной толщины «T», диа-

Y_{a —} y_{b — n}d/4                метра d и с уменьшением радиуса «г» гиба (мат-

Длины образующих параллелей, проходя-рицы, внутреннего обода).

щих через центры тяжести сечений А и В (для опре-      При этом в процентном выражении сте- деления объемов с сечением А и сечением В), со-пень утонения «С» составляет величину: ставят нижеследующие усредненные значения «С» = (1/T) 100% — d/(2г + d) 100%.      (2)

(рис 6 )•                                            Напряжения растяжения в стенке трубы

Yam — п{г + d/2[1-(Sin ф)/ф]};          вычисляются по известным соотношениям:

Y bm — п{г + d/2[1+(Sin ф)/ф]}.                         ^W1 = Yd 2U^-D;

W2 = Р т d/2T.

Здесь

W1 – напряжения растяжения для гиба толщиной (T-t);

W2 – напряжения растяжения для гиба толщиной T;

Р т - давление в трубопроводе диаметром d.

Оценка корректности математической модели утонения толщины стенки изгибаемой трубы

Проведем сравнение полученного нами результата с известными экспериментальными и теоретическими материалами ряда исследователей.

В работе Козлова А.В., Шеркунова В.Г. [14] приводятся теоретические данные компьютерного моделирования процесса утонения стенки трубы диаметром 60 мм, выполненной из стали 20, а также материалы экспериментальных замеров, проиллюстрированные на рисунках 7 и 8.

Для сравнения наших результатов на рисунке 3.8. приведены данные, рассчитанные по полученному упрощенному уравнению (1).

Достаточно хорошее схождение всех трех графиков свидетельствует о близкой точности расчетов.

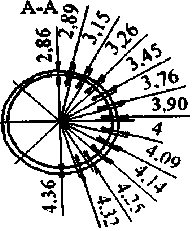
Рисунок 7 – Результаты экспериментальных замеров толщины стенки изогнутой трубы диаметром d = 60 мм, исходная толщина стенки Т = 4 мм, радиус гиба r = 2,5 d = 150 мм в сечении максимального утонения

Оценка порядка величины «C» по полученному соотношению (2), дает для трубы диаметром d = 60 мм и радиуса гиба «r» = 150 мм, значение С = [60 / (2·150 + 60)]·100% = 16,7%, что хорошо согласуется с литературными данными [14], составляющими 19,5%.

Основанием для принятия решения о возможности и условиях дальнейшей эксплуатации технического устройства (оборудования) являются результаты оценки его остаточного ресурса [21, 22].

Воспользуемся для оценки степени увеличения ресурса и долговечности материалами работ [12, 13]. В этих публикациях представлены результаты расчета напряженно-деформированного состояния гибов паропроводов с применением модифицированной формулы Содерберга для описания процессов ползучести при больших длительностях нагружения. Расчеты проведены методом конечных элементов для наиболее распространенных при изготовлении паропроводов марок сталей: 12Х1М1Ф, 15Х1М1Ф, 10Х9МФБ.

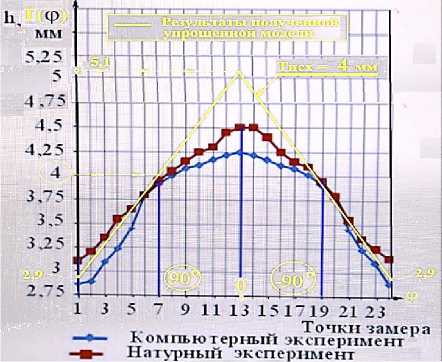
Рисунок 8 – Сравнительные результаты компьютерного моделирования, экспериментальных замеров по данным исследования [14] и разработанной аналитической модели изменения толщины стенки трубы при изгибе

Индивидуальный ресурс для гибов паропроводов определялся исходя из следующего соотношения гарантированных характеристик длительной прочности, представляющего собой преобразованное параметрическое уравнение [22]:

Lg (т) = ^^о^фк + Lg (q) — b. (3) где τ – индивидуальный ресурс, ч; q – используемая в расчете температура, K; n – коэффициент запаса прочности (n = 1,5); w – принимается равным интенсивности напряжений, МПа; b – постоянная, зависящая от (12Х1МФ – 24,88;

15Х1М1Ф – 25,20). Полином шестой степени представляет собой аппроксимирующую функцию модифицированного параметра Ларсона-Миллера (табл. 1).

По результатам вычислений было установлено, что увеличение внутреннего давления (то есть напряжений) р1/р2=1,5 раза, с 4 до 6 МПа, приводит к уменьшению ресурса с R 1 =2,489·10⁷ до R 2 =3,352·10⁵ ч. То есть R 1 /R 2 =74 раза.

Отметим, что соотношение напряжений в стенке гиба трубы обратно пропорциональны

В.В. Пеленко, Т.Ю. Короткова, В.Г. Злобин толщинам стенки, поэтому для любого значения давления в трубе можем записать:

(W1/W2) = Т/(Т–t).   (4)

Здесь W1 – напряжения растяжения в стенке гиба толщиной (Т–t);

W2 – напряжения растяжения в стенке гиба толщиной Т.

Таблица 1 – Коэффициенты аппроксимирующего полинома Ларсона-Миллера

Марка стали

А 0

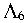
е s

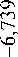
Соотношение толщин стенки гиба трубы Э =Т/(Т–t) =3,75/3,17=1,18 до и после утолщения (на 18%), получаем на основании формул (1), (2) и данных рис.8.

Таким образом соотношение напряжений в гибе трубы принимает величину (W1/W2) =1,18.

Полученное значение дает возможность, воспользовавшись логарифмической зависимостью (3) и экспериментальными цифрами соотношений р1/р2 и R 1 /R 2 , оценить увеличение ресурса гиба Rг 2 /Rг 1 , которое может быть определено методом подобия по уравнению:

Rг 2 /Rг 1 = Lg [(R 1 /R 2 )/(р1/р2)] ·[ (W1/W2)/(р1/р2)].

С учетом соотношения (5), окончательно получим:

Rг 2 /Rг 1 = Lg [(R 1 /R 2 )/(р1/р2)] ·[( Т/(Т– t)/(р1/р2)]. (5)

Вычисления по соотношению (5) дают следующее значение повышения ресурса трубы за счет увеличения толщины стенки гиба:

Rг 2 /Rг 1 = [Lg (74/1,5)] ·( 3,75/3,17)/1,5 = 3,07.

Таким образом, вычисляя по соотношению (1) величину утонения толщины «t» стенки трубы в результате гиба и увеличивая ее до исходного значения «T», можно увеличить ресурс трубы примерно в 3 раза.

• 1.    Построена физическая модель процесса утонения толщины стенки гиба.

• 2.    Разработана стереометрическая математическая модель деформации трубы при ее изгибе и получено уравнение для упрощенного расчета величины утонения.

• 3.    На основании сравнения с литературными источниками показана удовлетворительная точность полученной модели.

• 4.    Оценка повышения ресурса, проведенная по известной модели Ларсона – Миллера, показала возможность его увеличения в три раза, при обеспечении требуемой исходной толщины стенки трубы, увеличенной на 18% в ее утоненной части.