Повышение грузоподъемности ракеты-носителя путём оптимизации стратегии управления расходованием топлива

Основными возможностями дальнейшего повышения энергетических характеристик жидкостных РН являются следующие [3]:

• -    реализация полной выработки топлива жидкостной ракеты, когда двигатели нижних ступеней выключаются по уровнемерной информации СУРТ так, чтобы обеспечить возможно меньший остаток топлива в баках этих ступеней, а двигатель последней ступени выключается только по текущей информации о траекторных координатах с тем, чтобы обеспечить требуемые конечные условия выведения полезной нагрузки;

• -    программирование (систематическое изменение во времени работы двигателя) текущего соотношения K массовых расходов компонентов топлива ракетного блока. Возможность повышения энергетических характеристик РН посредством программирования K ( t ) соотношения расходов компонентов топлива появляется в случае, когда соотношение K _ном но- Чадаев Александр Иванович, кандидат технических наук, старший научный сотрудник лаборатории терминальных систем управления. E-mail: vladguc@ipu.ru Тропова Елена Ивановна, научный сотрудник лаборатории терминальных систем управления.

минальных масс рабочих запасов топлива на ракетном блоке не совпадает с тем соотношением K^* , которое соответствует максимальному удельному импульсу тяги жидкостного ракетного двигателя (ЖРД).

В данной же статье рассматривается возможность повышения грузоподъёмности моноблочной жидкостной РН, связанная с переходом от классической (традиционной) стратегии управления расходованием топлива, исходящей из приоритета критерия минимизации случайных отклонений δ K ( t ) от номинала коэффициента соотношения расходов компонентов топлива, – к обновлённой стратегии с приоритетом критерия минимизации потерь в грузоподъёмности ракетного блока, вызванных отклонением удельного импульса тяги из-за случайных отклонений δ K ( t ) в процессе регулирования опорожнения баков.

Удельный импульс тяги большинства применяемых в ракетной технике маршевых двигателей РН в характерных для использования таких двигателей режимах слабо зависит от соотношения массовых расходов компонентов топлива. Регулирование опорожнением баков ракет с такими двигателями производят с использованием стратегии управления, предусматривающей – с целью минимизации отклонения (от номинала) соотношения расходов – линейное умень- шение рассогласования объемов жидкостей в баках до нуля в момент опорожнения баков.

Другими словами, считают, что потребное для компенсации рассогласования объемов (а точнее, оценки рассогласования) отклонение соотношения массовых расходов от номинального для двигателя значения К _ном коэффициента соотношения расходов должно быть постоянным в течение процесса регулирования. Подчеркнем, что сказанное относится лишь к стратегии, «тенденции» управления. В реальных условиях действие случайных помех и возмущений существенно искажает описанную идеальную картину процесса регулирования опорожнения баков. Тем не менее, эта стратегия является оптимальной для ракет с двигателями, удельный импульс тяги которых мало зависит от соотношения массовых расходов компонентов топлива в диапазоне его изменения при регулировании опорожнения баков.

Для тех двигателей, которые характеризуются сильной зависимостью удельного импульса тяги от соотношения расходов, оптимальная стратегия управления расходованием топлива будет иной.

Отклонение δ K коэффициента соотношения расходов от номинального значения К _ном , возникающее при регулировании опорожнения баков, обычно приводит к уменьшению удельного импульса тяги и, следовательно, к потерям в скорости. Величина К _ном , как правило, весьма близка (или в точности равна) тому значению К^* соотношения, при котором достигается максимальное значение удельного импульса тяги двигателя. Однако влияние отклонения удельного импульса тяги на скорость ракеты зависит от текущей массы G ( t ) ракеты: оно увеличивается к концу работы ЖРД. Поэтому, очевидно, оптимальная стратегия управления расходованием топлива должна приводить к повышенным отклонениям δ K в начале процесса регулирования опорожнения баков (когда влияние удельного импульса тяги на скорость ракеты относительно мало) и меньшим отклонением δ K к концу процесса.

ПОСТАНОВКА ЗАДАЧИ

В отличие от [2] будем учитывать начальные возмущения в виде начального рассогласования объёмов компонентов топлива.

Перейдем к математической постановке задачи. Положим, что в процессе регулирования опорожнения баков в момент времени t вычисляется некоторое потребное для компенсации относительного рассогласования δV(t) объемов компонентов топлива относительное отклонение коэффициента соотношения расходов δKзад(t). Это означает, что функция δK(t), характеризую- щая регулирование опорожнения баков на интервале те(t, T), должна удовлетворять условию

T

T^ 18 K ( т ) d т = 8 K „ ( t ) .       (1)

Будем определять функцию δ K ( τ ) такую, чтобы изменение кажущейся скорости РН Δ W , вызванное уменьшением удельного импульса тяги в процессе регулирования опорожнения баков было минимальным:

A W [ 5 K ( т ) ] = min .           (2)

Условие (2) с учетом типовой аппроксимационной зависимости удельного импульса тяги J _уд (на безатмосферном участке полета РН) от коэффициента соотношения расходов компонентов топлива

J уд = J _но „ (1 + a 5 K ² + b 5 К ) , (3)

где Jном – номинальное значение Jуд ; α, b – коэффициенты аппроксимационной зависимости, представим в виде

T

^Д W = j

t

gJ ... ( a 8 K ²( т ) + b 8 K ( т )) Gd _т ,

G ( т )

где g – ускорение силы тяжести; G (t) – текущее значение массы РН; G - номинальное значение суммарного расхода компонентов топлива.

Для нахождения функции δK(t) на интервале те [t,7] для всех возможных t достаточно найти 5K(t) на интервале те [О,T. Введем вспомогательную переменную x (t) = у j 6K (т) dт ,

T О при граничных условиях х(О) = О, х(T) = 6Kзад, и будем определять функцию x(t), обеспечиваю- щую минимум функционала

J е ( t ) dt = [ ^g J "°” ⁽ “x ⁽ t ^} T ⁺ bx ⁽ t ^} T ) G i dt , ^{j j}              G ( t )

x '( t ) = dxf¹ .(4) dt

Уравнение Эйлера для функционала (4) имеет вид d^S^t) = О .            (5)

dt d x

Решая уравнение (5) с учётом взятия частной производной по x‘ от подынтегрального выражения (4) [4] получаем d ( ax,2(t)T2 + bx‘(t)T ) dX^ [gJ - G (t)      )

^gJ HOM

2 ax T ² + bT G ( t )

При дифференцировании по t правой части соотношения (6) и использовании равенства (см. (5))

d dt

^gJ ном

к

2 axT ² + bT 1

G ( t ) ,

= 0

получаем dx'(t)

b x (t) +----

2 aT

^^^^^^^e

dG ( t ) a ------= 0 .

G ( t )

Интегрируя (7), получаем

In i x ' (t ) +

b

2 aT

1 - ln ( G ( t ) ) = In C ₁

(С ₁ – произвольная постоянная), откуда следует

b

x 't t ) = C ₁ G ( t ) -

2 aT

.

Интегрируем (8) с учетом,

G (t) = G ₀ - Gt , G = const :

что

t x (t) = JlC, G (т)

0 к

^^^^^^^^

= C , G 0 т

t

^^^^^^^^

. т2

CG —

¹ 2

t

b т t

^^^^^^^B

2 aT 0

= C , G 0 1 - C , G 2

^^^^^^^B

— + C . 2 aT

С использованием граничных условий x (0) = 0, x ( T ) = δ K _зад определяем входящие в (9) постоянные интегрирования:

5 ^K зад

C = 0,

C i =

b

+--

2 a

■ T1

G^T - G ⁰        2

После подстановки С и С1 в (9) получаем x (t) =

2 f 8Kaд+ b зад к______2a

T (2 G ₀ - GT )

²) G_nt - G — I - ⁰ 2 )

b

2 aT

t . (10)

Дифференцируя x ( t ) по t , с учетом равенства 8 K ( t ) = x ( t ) T получаем

3 K ( t ) =

2 | 8 K зад

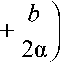
2( G 0 - GT )

G ⁽ t ^{) -}

b

2a

²⁸ K зад ^{G (} t ⁾ + A f 2GVL - 1 |

G 0 + G _K    2a к G 0 + G _K    J

. (11)

После введения обозначений

G ( t ) H = —, G 0

₌ G ( T ) ^ K

^G 0

уравнение (11) приводится к виду

8 K ( t ) = ^ K ^ + Ь- ^f 2-±- - 1 1 , (12)

• 1    + Цк    2a к 1 + Hk J

где µ – текущее значение относительной массы РН; µ _к – конечное значение этой массы.

Таким образом, оптимальная стратегия управления расходованием топлива моноблочной жидкостной РН предопределяет – в условиях отсутствия ошибок измерения и параметрических возмущений – линейное (относительно текущей массы РН) изменение соотношения расходов компонентов топлива в соответствии с законом (12).

АНАЛИЗ ОПТИМАЛЬНОЙ СТРАТЕГИИ УПРАВЛЕНИЯ РАСХОДОВАНИЕМ ТОПЛИВА РН

• 1.    Первый член в законе (12):

• 8 K ( t ) = ^^{8 К за}^ ц ,          (13)

• 1    + Hk

где 8 K _зад =- 8 V (0) , задает оптимальную (по критерию (2)) стратегию регулирования опорожнения баков при парировании действия на процесс расходования топлива случайных возмущающих факторов (в данном случае – случайного начального рассогласования объемов δ V (0) компонентов топлива). В отличие от используемой ныне в РКТ стратегии

8 K ( t ) = - 8 V (0) ,           (14)

обеспечивающей синхронизацию опорожнения баков окислителя и горючего ракетного блока при минимальном отклонении δ K от номинала коэффициента соотношения расходов компонентов топлива, стратегия (13) при своем исполнении приводит к повышенным (сравнительно с (14)) отклонениям от номинала соотношения расходов компонентов топлива на начальном участке регулирования опорожнения баков и к пониженным – на конечном участке. В частности, при исполнении стратегии (13)

• 8 K (0) = - A-8 V (0),

• 1    + H k

8 K(T ) = - ^2u- 8 V (0), Ц к ^ 1

• 1    + Hk

В вырожденном случае µ _к = 1 обе стратегии ((13) и (14)) совпадают.

Для численного оценивания эффективности перехода от традиционной стратегии (14) регулирования опорожнения баков к оптимальной стратегии (13) рассмотрим набор гипотетических ракетных блоков ( µ _к = var ) с одним и тем же ЖРД, номинальное соотношение К _ном расходов компонентов топлива в котором совпадает с оптимальным К^* : тогда в формуле (3) b = 0 и

A J = J уд - J ho. = a § K ²’ a <  0.    (15)

Введем безразмерный коэффициент r = A Gnr /G ПГ a 8K \J ho. ’ характеризующий относительное отклонение массы GПГ полезного груза ракетного блока, вызванное снижением (15) удельного импульса тяги при регулировании опорожнения баков.

В табл. 1 представлены результаты расчетов коэффициента r при двух стратегиях (традиционной (14) и оптимальной (13)) регулирования опорожнения баков для ракетных блоков, ха- рактеризуемых различными значениями параметра Цк = G(T)/Gо.

Данные таблицы показывают, что компенсация случайного рассогласования δV(0) объемов компонентов топлива посредством изменения соотношения расходов в соответствии с (13) позволяет уменьшить случайные потери ΔGПГ в массе полезного груза по сравнению с традиционной стратегией (14) регулирования опорожнения баков, предусматривающей постоянное в процессе опорожнения отклонение соотношения расходов компонентов топлива от номинального значения. Из таблицы также следует, что выигрыш Δr от применения оптимальной стратегии

• (13)    тем выше, чем меньше значение µ _к , т.е. чем совершеннее конструкция ракетного блока.

2. Второе слагаемое в законе (12)

8 K ( t ) = b 2-*1 ² a ( ¹ + u , J

отражает возможность повышения энергетических характеристик ракетного блока за счет программного (систематического) изменения (во времени работы ЖРД блока) соотношения рас- ходов компонентов топлива. Впрочем, правильнее было бы утверждать, что соотношение (16) указывает на возможность снижения потерь в энергетике ракетного блока, вызванных смещением – относительно номинального (заправочного) коэффициента соотношения Кном – того значения К* соотношения расходов компонен- тов топлива, при котором достигается максимум удельного импульса тяги ЖРД (см. (3)):

b

HOM

2 a

*         *

A K = K - K

-

Диапазон программируемого изменения (16) соотношения δK(t) в процессе опорожнения баков от 8K (0) = — 1-Цк

2 a 1 + цк до 8K (T) = - — 1-Цк-2 a 1 + цк тем больше, чем сильнее отличие K* от Kном (см. (17)) и чем «совершеннее» конструкция ракетного блока, т.е. чем меньше относительная конечная масса µ(T) = µк блока; в предельном случае при µк = 0 опорожнение баков должно заканчиваться при K(T) = K* .

ЗАКЛЮЧЕНИЕ

Таким образом, энергетические характеристики жидкостной моноблочной РН могут быть повышены путём программирования изменения относительного отклонения от номинала коэффициента соотношения расходов компонентов топлива, а именно, повышенных отклонений на начальном участке регулирования опорожнения баков и пониженных – на конечном участке.

Таблица 1. Значения коэффициента r при традиционной и оптимальной стратегиях регулирования

Ц к	Величина r при стратегиях регулирования опорожнения баков		Выигрыш в A r при переходе от традиционной к оптимальной стратегии
	традиционной (14)	оптимальной (13)
0,4	1,31	1,23	0,08
0,3	1,71	1,54	0,17
0,2	2,30	1,90	0,40
0,1	3,28	2,49	0,79
0,05	4,28	2,62	1,66