Повышение эффективности теплообменных аппаратов

Государственная программа по энергосбережению и повышению эффективности промышленности, принятая в 2010г. правительством РФ предусматривает использование и внедрение энергосберегающих технологий и реализующих их конструкций энергопотребляющих установок и теплопередающих аппаратов. Это позволит снизить энергоемкость ВВП РФ. При условии непрерывно растущей потребности экономики в энергетических и материальных ресурсах энерго- и ресурсосбережение можно представить, как рациональное использование энергетических потоков и ресурсов на различных уровнях технологического производства. Одним из очевидных направлений в энергосбережении является повышение эффективности технологического оборудования путем совершенствования теплопотребляющих и теплопередающих аппаратов и устройств [1].

В данной статье исследуется возможность повышения эффективности теплообменных аппаратов различных конструкций, предназначенных для передачи теплоты от воздуха к теплонесущим поверхностям теплообменных аппаратов, или, наоборот, путем установки ин- тенсифицирующих устройств, способствующих закручиванию потока воздуха. Интенсификация процессов теплообмена способствует повышению характеристик всего технологического процесса производства тепла в энергетических установках. Активные исследования в области интенсификации процессов теплоотдачи обусловлены значительным достигаемым эффектом. Однако количественная оценка эффекта в значительной мере затруднена тем, что моделирование процесса вынужденного конвективного переноса теплоты является одним из сложных в теории теплопереноса и связано с определением множества факторов, оказывающих влияние на процесс [2 – 3].

Конвективный теплообмен, т. е. процесс переноса теплоты, происходящий в движущихся текучих средах, обусловлен совместным действием двух механизмов переноса тепла – собственно конвективного переноса и теплопроводности. В большинстве случаев (при безотрывном обтекании) роль конвективного переноса весьма велика по сравнению с теплопроводностью. Теплопроводность влияет лишь на распределение температуры по сечению потока.

Современные средства гидрогазодинамики

В настоящее время для решения задач процессов конвективного теплообмена, задач в области гидрогазодинамики и тепломассобмен-ных процессов применяют специальные пакеты вычислительных программ. Среди них наиболее часто используются такие, как Comsol, MSC/Nastran, CFX, Fluent, Star-CD, LS-Dyna, Ansys, Abaqus, Flow Vision, MSC/Marc, Magmasoft, SolidWorks/Flow simulation и др. В этих программах используются различные методы дискретизации расчетных областей (построение сеток, выделение конечных объемов, конечных и граничных элементов [4] и др., которые позволяют производить дискретизацию расчетных областей и отслеживать движение частиц среды в пространстве и во времени с любой, наперед заданной, точностью. Эффективность этих методов подтверждается многими исследованиями[5–8].

В данной статье в качестве средства моделирования нами рассматривается прикладной программный пакет SolidWorks и в частности его модуль для моделирования течения жидкостей и газов – Flow Simulation. Flow Simulation– наиболее доступное программное обеспечение, полностью интегрированное в SolidWorks, предназначенное для расчёта движения потоков газов и жидкостей, как во внутренних каналах, так и при обтекании твердотельных моделей, построенных в CAD-среде SolidWorks. Здесь с помощью технологий вычислительной гидрогазодинамики ((Computational Fluid Dynamics (CFD)) реализованы расчеты теплопередачи путем конвекции (естественной и вынужденной), излучением и теплопроводностью. Flow Simulation моделирует движение потока, на основе решения уравнений Навье-Стокса [4 – 5], которые являются интерпретацией законов сохранения массы, импульса и энергии для потока жидкости (газа). Уравнения дополнены выражениями состояния жидкости, которые определяют природу жидкости или газа и эмпирическими зависимостями их плотности, вязкости и теплопроводности от температуры. Несжимаемые неньютоновские жидкости рассматриваются по зависимости их динамической вязкости от скорости деформации сдвига и температуры, а сжимаемые жидкости рассматриваются по зависимости их плотности от давления. Ещё одна часть уравнений отвечает за геометрию потока, граничные и начальные условия.

Пограничный слой

В реальных условиях обтекания поверхности потоком жидкости или газа на поверхности тела формируется пограничный слой – область течения, в котором происходит основное изменение скорости. Толщиной пограничного слоя жидкости или газа 6 принято называть область поверх внешнего края слоя газа или жидкости, определяемого как 99% свободной скорости потока.

В случае ламинарного течения профиль скорости в этой области легко рассчитать по уравнениям Навье – Стокса. Однако для большинства практических случаев обтекания поверхностей, имеющих сложный геометрический профиль характерна турбулизация потока.

В случае турбулентного движения пристеночная область потока разделяется на подслои (рис. 1, а). Переход между тремя режимами течения в погранслое определяется числом Рейнольдса, Rе = рlu/р, где р- плотность жидкости, I - характерный линейный размер (например, гидравлический диаметр); —- скорость, и -- динамический коэффициент вязкости.

Рассмотрим, например, воздух. Кинематическая вязкость v = ^/^=1,510 —5 м²/с. Переход от ламинарного режима течения к турбулентному осуществляется, в зависимости от типа течения, при числе Рейнольдса Rе ~ 10 2 ^10 5 . Это означает, что переход происходит при произведении линейного масштаба на скоростной lit ~ 10 —3 -100 м²/с, что весьма немного.

Легко убедиться, что в таких задачах как обтекание регулярных поверхностей потоком воздуха от вентилятора течение является турбулентным.

Похожий эскиз можно выполнить для температурного переноса от температуры поверхности к температуре потока (рис. 1, б). Причем, толщина термического пограничного слоя не обязательно должна быть той же, что у жидкости или газа. Основным уравнением, описывающим процесс теплоотдачи от жидкости или газа к твердой поверхности является уравнение Ньютона – Рихмана:

Q = а A (T_s - ТД             (1)

где: Q - количество теплоты, которое отводится от поверхности охлаждаемого или нагреваемого тела, Вт; а - коэффициент теплоотдачи, Вт/(м2.K), который не является термодинамическим свойством, а представляет собой упрощенное соотношение для состояния газа или жидкости и условий на поток, и потому часто называется потоковым свойством; л – площадь поверхности.

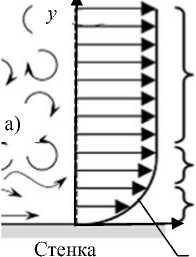
Область развитой турбулентности

Буферный слой (область логарифмического закона) Ламинарный подслой

u ( y )

^y 4

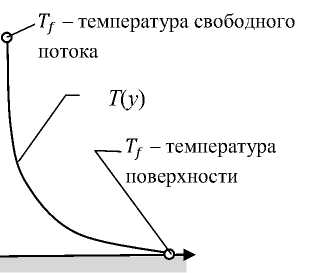
Стенка горячая

Рисунок 1 – Параметры пограничного слоя : а) – относительная скорость потока; б) – температура

Теплоотдача является сложным процессом, коэффициент теплоотдачи зависит от большого количества факторов, находящихся в определенной зависимости друг от друга. Актуальный механизм теплопередачи через пограничный слой принимается как проводимость по направлению оси у через стационарную жидкость рядом со стенкой, равная скорости конвекции от пограничного слоя к самой жидкости ли газу. Это можно записать так:

«Л (T_s - Tf) = - кА ("/dy)⁵ , (2) где к – коэффициент конвекции. Таким образом, коэффициент конвекции для заданной ситуации может быть оценен измерением скорости теплопереноса и разницы температур или вычислением температурного градиента, примыкающего к поверхности, и разницы температур.

Определение коэффициентов теплоотдачи

Определение коэффициентов теплоотдачи является одним из основных задач для определения эффективности методов интенсификации процессов теплопереноса. Интенсив- ность процессов теплообмена изменяется по поверхности тел при относительном движении жидкости (газа) и обтекаемой поверхности, поэтому коэффициент теплоотдачи тоже изменяется, поэтому вводится местный коэффициент теплоотдачи:

dQ

q

α =            =         ․

(^TS - т_гур ⁼    - ^ТА ^․

Таким образом, коэффициент теплоотдачи есть плотность теплового потока q на поверхности тела, отнесенная к разности температур поверхности тела и окружающей среды.

На практике для расчетов обычно применяют средний коэффициент теплоотдачи. В общем виде коэффициент теплоотдачи зависит от следующих факторов: от вида теплоносителя, его теплофизических свойств и температуры; от температурного напора; вида конвекции и режима течения; от состояния поверхности и направления обтекания; от геометрии обтекаемого тела и т.д. Также коэффициент теплоотдачи зависит от природы возникновения движения среды.

а =   ( и , Р , С р , Р , &) , Р , д , L ,Ф…), (4)

где: и – скорость жидкости, м/с; р – плотность жидкости, кг/м3; λ – коэффициент теплопроводности жидкости, Вт/ м К; μ – коэффициент динамической вязкости жидкости, м2 /с; ср

–

удельная массовая изобарная теплоемкость жидкости, Дж/ (кг К); β – коэффициент объемного расширения жидкости, К ^-1; g – ускорение свободного падения, м²/с; L – характерный линейный размер поверхности обтекаемого тела, м; Ф – геометрическая форма тела.

Практически не существует возможности определения математической зависимости коэффициента теплоотдачи от многочисленных факторов, поэтому для расчета коэффициента теплоотдачи используют Критерий Нуссельта Nu является характеристикой теплообмена на границе между жидкостью и стеной:

Nu=αL, (5) λ где: L – характерный линейный размер, λ – коэффициент теплопроводности окружающей среды. Для стационарного процесса критерий Нуссельта находят, используя критериальное уравнение конвективного теплообмена, в котором числа подобия имеют определенный физический смысл и рассматриваются как обобщенные переменные:

Nu = л Re m Pr ^{п £}т ^⋅ s_L ,

где: Nu, Re, Pr – числа подобия Прандтля; Л,m,п – коэффициенты, зависящие от вида процесса теплоотдачи, определяемые экспериментальным путем; ^L – коэффициент, учиты- вающий изменение среднего коэффициента теплоотдачи по длине; тт - коэффициент, учитывающий зависимость теплофизических свойств от температуры:

= (Pr ж / Pr ст ) ^, , (7)

Приближенное математическое описание процессов теплопереноса в пограничном слое связано с моделями Прандтля, Ландау, Левича и Кармана и др., а также с гидродинамическим подобием и аналогией Рейнольдсом и Чилтон - Колборном. Так для определения усредненных значений коэффициентов теплоотдачи в каналах с закруткой потока авторами [3] предложено использовать модель пограничного слоя с функцией турбулентной вязкости Дайслера с учетом затихания турбулентных пульсаций по модели Ландау и Левича.

Для определения коэффициентов теплоотдачи были приняты следующие допущения:

• -    входной участок значительно меньше длины канала;

• -    теплофизические свойства теплоносителя поперек пограничного слоя изменяются незначительно;

  - основное сопротивление процессу теп-

• лоотдачи происходит в пограничном слое, в котором происходит молекулярный перенос теплоты в сочетании с затухающей турбулентной диффузией (модель Ландау - Левича);

• -    турбулентное число Прандтля примерно

равно единице.

Процесс передачи теплоты записан в виде [2]:

b = 2,5; R ' = 30; с= 0,14 - безразмерные величины, связанные с областью интегрирования.

Показатель степени при числе Прандтля Pr⁰ ■ ⁶⁶ следует из закона затухания турбулентных пульсаций в пограничном слое. Уравнение (9) является общим и позволяет определять коэффициент теплоотдачи для различных условий турбулентного движения теплоносителя при соответствующих значениях его параметров.

В частности, для случая обтекания вдоль плоской пластины потоком в турбулент- ном режиме параметры, входящие в уравнение (9) имеют следующий вид [3]: для динамической скорости и = й^ с^/2, где: й - средняя скорость движения среды, м/с; с^ - коэффициент трения определяется по зави- симости cz = 0,455/aogReJ2,5 8;

ReL=Pй LIp,(12)

где:  - определяющий размер процесса тепло- отдачи(длина пластины), м; - коэффициент динамической вязкости, Па с.

Средняя безразмерная толщина погра- ничного слоя определяется по следующей формуле [3]:

R5 = ехр (0,4 й/ и - 5,0)),(13)

или с учетом того, что 5 = 0,205 L /R о*²' ² ) ри 6

R5 =       ■(14)

На основании выражения (9) число Нуссельта для процесса теплоотдачи пластины:

Re ^с Pr

Nu ь = -----------------77v

13,91 Pr ․  +2,5ln + 0,14

Для поверхности в виде круглой трубы с гладкими стенками уравнения (14), (153) при- нимают следующий вид:

= 4,1 10 -

8  ;

Nu

Re Pr

13,91 Pr ․  +2,5ln +

0,14  ,

где ^ - коэффициент сопротивления для осеси- метричного потока.

Сравнение результатов расчетов числа Нуссельта по известным ранее формулам дает удовлетворительную сходимость для пластин от 0,4% до 16,2 %; для гладкой трубы от 2,8% до 7,9%.

Оценка изменения коэффициента отдачи от скорости потока в соответствии с (5,17) приведена в таблице 1

Таблица 1 – Зависимость коэффициента теплоотдачи от скорости потока

Скорость потока й , м/с	Расход, G , м3/с	Число Рейнольдса Re	Коэффициент теплоотдачи, Вт/(м2 К)
1	0,0683	19588,31	2,741814
3	0,2049	58764,94	23,26998
5	0,342	97941,57	29,34427
10	0,683	195883,1	45,83281
20	1,366	391766,3	73,68513

Из результатов расчета следует, что с увеличением скорости обтекания теплоотдача увеличивается (рис.2).

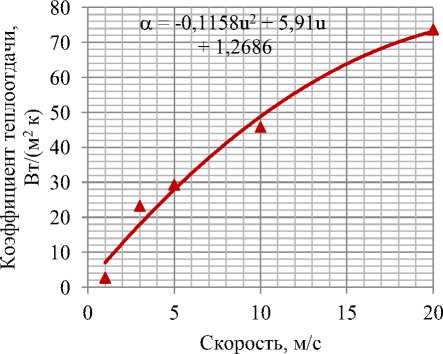
Рисунок 2 – Зависимость коэффициента теплоотдачи от скорости обтекания

Однако определение теоретическим путем коэффициента теплоотдачи для поверхностей с элементами интенсификации (шероховатость, выступы, накаты, выступы и т.д.) является достаточно сложной задачей.

Используя выражение (9) запишем его для закрученного потока при стационарном режиме. Среднее значение динамической скорости в потоке, закрученном для интенсификации выразим из условия бал анса сил в канале:

и =     з/(8соѕ 9 ),              (18)

где: 9 – угол закрутки потока; ^з – коэффициент сопротивления потока с закруткой.

В пограничном слое с интенсификацией параметры уравнения (9) имеют вид:

• к з= клД / f з, R з=30 41 /^з, ' Rs

=        ․              (19)

з

Выражение для определения числа Нуссельта для закрученного потока:

Re VI /((8соѕ) err

• ^{N u з =} 13,91Pr ․         +2․5ln +0․14 ^․

Данные выражения для числа Нуссельта (20) могут быть рекомендованы только для приближенных расчетов теплообменных аппаратов в случае, когда параметры движения среды относительно теплообменных поверхностей легко определить из опыта. В более общих случаях необходимо использовать сложные математические модели гидрогазодинамики, например, основанные на уравнениях Навье – Стокса [4, 7].

Выбор модели турбулентной вязкости

Для описания процессов взаимодействия текучих сред (жидкости или газа) с твердыми поверхностями, движение которых описывается уравнениями Навье – Стокса, применяют полуэмпирические модели турбулентной вязкости, которые в современных вычислительных продуктах разделяют на следующие группы:

• -    алгебраические модели;

• -    модели с одним дифференциальным уравнением переноса характеристики турбулентности;

• -    модели с двумя дифференциальными уравнениями переноса (двухпараметрические модели);

• -    модели с большим числом уравнений.

Основная идея моделей сводится к предположению о существовании средней скорости потока и и среднего отклонения от него и′, т.е. пульсационных скоростей, и=  + и',                    (21)

где:

C^t+ Δ t

й( X , ^ , 7. )=¹/_Δt J     ^U( X , У , 7 ) dt ; (22)

Δ t – период времени, существенно превышающий время формирования вихрей.

Алгебраические модели являются наиболее экономичными моделями турбулентности, используемыми при расчетах течений жидкости и газа. В их основе используется гипотеза Буссинеска или гипотеза турбулентной вязкости. В ней предполагается, что, по аналогии с вязкими напряжениями в ламинарных потоках, турбулентные напряжения также пропорциональны градиенту некой средней скорости. Эта гипотеза базируется на рассмотрении турбулентных вихрей как частиц, подобных молекулам в кинетической теории. Причем

эффициент турбулентной вязкости _т, кинетическую энергию турбулентности и скорость диссипации энергии е в виде:

т = ^{СС К}Ур Е- (27)

вихри крупных размеров передают свою кинетическую энергию вихрям меньших размеров. Вихри минимального размера диссипируют непосредственно в тепло. Их размер характеризуется так называемым колмогоровским мас

, штабом т] = — V J£1   , где г - местная ско рость диссипации на единицу массы, а v - ки

нематическая вязкость.

Наибольшее количество энергии при этом переносят вихри некоторого «среднего» размера. То есть, вихри заменяют молекулы в роли носителей тепловой энергии и количества движения. Для вязкого газа осредненное значение Рейнольдсовых напряжений для двумерно-

Для использования уравнений (26) -(27) необходимо задание интегрального масштаба турбулентности. Для определения масштаба турбулентности, как правило, используют дополнительные дифференциальные уравнения. Наиболее часто используются две модели расчета турбулентности: Спаларта - Ал-лмарса и к — е модель.

Модель Спаларта - Аллмараса относится к классу однопараметрических моделей турбулентности. Здесь появляется только одно до-

го потока можно записать в виде

___      /du\2 du т =-  ′ ′ =          = т ․(23)

полнительное уравнения для расчета вязкости Спаларта - Аллмараса. Компоненты тензора турбулентных напряжений определяются следующим образом:

Здесь: –координата, совпадающая с на-

правлением потока; у- поперечная потоку координата; ʼи ’–проекции пульсационной скорости на оси ии у, соответственно; L- масштаб турбулентности, который имеет порядок линейного размера крупных вихрей.. Вместо динамической вязкости ^ введен коэффициент турбулентной вязкости ^т, кт — Сгр4^Ч,              (24)

где V V ² - масштаб пульсаций поперечной скорости, возникающей от действия продольной. Очевидно, что коэффициент турбулентной вязкости в турбулентном потоке является переменной величиной и его определение практически невозможно. Т.е. представление Буссинеска

- ′ ′=2     ;    =    ;

χ

=         ; χ=  ․

χ +

Для вспомогательной величины записывается

уравнение переноса du

dt

…+  {∇∙[( + )∇ ]+   (∇ ) }

а

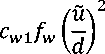
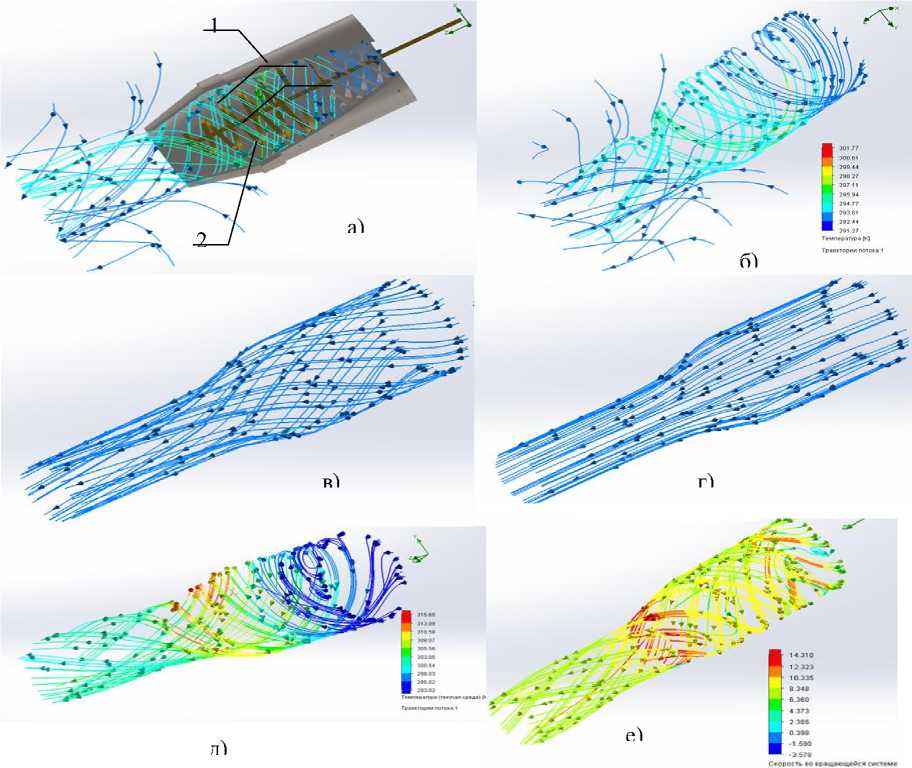
Здесь S- локальная величина завихренности,

≡ +

2 fu 2 , ^ - расстояние до ближай-

шей твердой границы.

не приводит к решению задачи, но записанное им выражение тензора турбулентных напряжений через параметры осредненного потока и называется моделью турбулентности.

Скорость диссипации энергии турбулентности е (м²/с³) выражают [11] через пульсационную скорость з? и масштаб пульсаций L.

′ ²

≈    ≈ т

В соответствии с гипотезой Колмогорова-Прандтля [9] е выражается при больших числах Рейнольдса через кинетическую энергию К и интегральный масштаб соотношением

Е-^С^"1 ^{= ⧸ ,}

где - эмпирическая постоянная. При этом получено [11] соотношение связывающее ко-

χ

+

1+

+

= χ

1 -L Г6 1 ' 6

1+

^Tw = ⁹ _а6 _{+ с}6      ;

+

_ Й                       А X z-x-xx

⁹     + ^Cw((-   — т) - (30)

На твердых стенках ставятся граничные условия =0. Константы этой модели турбу-

лентности cb1=0,1355; 7=2/3; с22=0,622; к=0,41; cw1 — сь2К + (1 + сь)М7; cW2=0,34; cw3 =2; смi=7,1.

Преимуществом этой модели является ее устойчивость и хорошая сходимость. По умолчанию для модели турбулентности Спа-ларта - Аллмараса установлено значение турбулентной вязкости равное 0,001 м2/с. Эта величина примерно соответствует параметру для воздуха при стандартной температуре и атмосферном давлении.

Вк-е модели турбулентности записы- метрической формы. Например, к-е модель ваются два дополнительных уравнения для расчета кинетической энергии турбулентности К и скорости диссипации кинетической энергии Е.

С точки зрения теории размерностей можно предположить, что отношение К / Е и есть то время, за которое энергия движения крупных вихрей, полученная от осредненного движения, проходит весь спектр масштабов размеров – от наиболее крупных до самых мелких, при которых и происходит диссипация турбулентной энергии. Т.е. т , входящее в уравнение коэффициента турбулентной вязкости равно:

т=    ́,(31)

где К – турбулентная кинетическая энергия

Отсюда следует, что коэффициент турбулентной вязкости определяется по формуле:

кт=СцРК2/́․(32)

Кроме того, в модель входят следующие уравнения:

Т ( РК)+= д / /л т\ ЭК]

…=      ^т+д)^— + Pk ^- РЕ ; (33)

OXj \@к' vXj

• 9 , . . д , _ ,

( рЕ)+=⋯ д //лт     \ Эе 1

…= т₊ р кт +⋯

OXj L \сг£

Е

…+  (Cel - C£2ps)․(34)

IX

В классической k - Е модели по умолчанию используются следующие числовые константы: С = 0,09; °К = 1; а_£ = 1,3; ^£1= 1,44; С_£2 = 1,92.

Эта модель широко используется для свободных течений (струи, слой смешения и т.п.), но плохо описывает пристеночные течения. Дело в том, что при выводе основных уравнений, относящихся к скорости диссипации ε , использовалось допущение о больших значениях локального числа Рейнольдса. Возле стенки это допущение нарушается – локальное число Рейнольдса стремится к нулю.

Буферный слой не моделируется, для расчета скорости у стенки используются пристеночные функции. Благодаря быстрой сходимости и относительно низким требованиям к объему памяти к-Е модель очень популярна при решении промышленных задач. Она не очень точна при моделировании течений с положительным градиентом давления, струйных течений и течений в области с сильно искривленной геометрией. Модель хорошо подходит для решения задач обтекания тел сложной гео- рекомендуется использовать для моделирования потока вблизи плохо обтекаемого тела.

Интенсивность турбулентности является мерой пульсаций в данной точке потока. Интенсивность турбулентности изменяется от 0 – 3% в атмосфере до 7 – 8 % и более в машинах.

Конкуренцию перечисленным обеим моделям, особенно при расчете пристеночных эффектов в гидрогазодинамике, составляет двухпараметрическая, так называемая, двухзональная к - О) модель Ментера [10]. В последнее время для моделирования процессов гидрогазодинамики применяют также гибридные модели, совмещающие в себе несколько моделей турбулентности и построение пристеночных функций в различных слоях пограничного слоя, а также прямое численное моделирование (DNS – Direct Numerical Simulation) и моделирование крупных вихрей (LES – Large Eddy Simulation). Применение и развитие этих подходов связано с развитием вычислительных рессурсов современных ЭВМ.

Постановка и решение задачи теплообмена в CAD/CAE – среде

Процесс постановки и решения задачи теплообмена в CAD/CAE – среде можно представить следующим алгоритмом:

• -    построение геометрии объекта (например, в SolidWorks);

• -    определение границ расчетной области, ее физических свойств;

• -    разбивка области на подобласти, построение сетки (например, во Flow Simulation);

• -    постановка граничных условий⁴ и выбор модели турбулентности;

• -    задание цели проекта, запуск и проведение расчёта;

• -    контроль точности результата (сходимости расчетов);

• -    просмотр и анализ результатов полученного решения.

Поскольку большинство перечисленных процедур в современных САD/САЕ – системах формализованы "встроенными" системой уравнений и методом их анализа, то наибольшую трудность в процессе применения численного анализа вызывают постановка граничных условий. Для исследования интенсивности теплопередачи при конвективном теплообмене наибольшую трудность представляет собой определение коэффициентов теплоотдачи либо вы- бор моделей турбулентности, определяющих теплопередачу через пограничный слой потока к стенке твердого тела. В SolidWorks/ Flow Simulation последняя задача сводится к определению параметров турбулентности к-Е модели для входного и выходного потоков.

В качестве рекомендаций к выбору параметров многие авторы указывают на то, что для разрешения некоторой неопределенности в отношении одного или нескольких входных значений параметров турбулентности, необходимо проведение качественного исследования путем повторного расчёта с использованием одного или нескольких различных значений неизвестных переменных. Это позволит определить, насколько существенно их влияние на результаты моделирования. При этом использование настроек по умолчанию допустимо для модели турбулентности Спаларта – Аллмараса, где значение турбулентной вязкости соответствует параметрам стандартной атмосфере и степени турбулентной вязкости 70, характерной для большинства теплообменных аппаратов.

Как правило, большинство задач строится таким образом, чтобы на входе и выходе не требовалось подробного задания параметров турбулентности с помощью профилей переменных по пространству, поэтому в большинстве задач для течений в каналах при условии применения к - Е модели рекомендуется задавать интенсивность турбулентности и гидравлический диаметр, понятие которого связано с входным поперечным сечением трубы или воздуховода.

Интенсивность и масштаб длины – этот подход предпочтительно использовать в тех случаях, когда можно достаточно легко оценить турбулентный масштаб длины. Один из примеров таких задач – поток ниже по течению после обтекания препятствий, таких как поворотные лопатки или перфорированные пластины (масштаб длины примерно равен размеру отверстия, через которое проходит поток). Ещё один пример – поток в пограничном слое (масштаб длины примерно равен 40% толщины пограничного слоя). При моделировании задач внешнего обтекания для свободных границ рекомендуется устанавливать значение интенсивности турбулентности меньше или равное 1% и значение степени турбулентной вязкости равное 2.

Интенсивность турбулентности может быть определена путём измерения или из имеющихся статистических данных. При отсутствии такой дополнительной информации рекомендуется умеренное значение для интенсивности турбулентности (4 – 5%). После прохождения препятствий интенсивность турбулентности потока, как правило, высока. Если имеются дополнительные данные о течении, то их можно использовать для задания параметров турбулентности. В случае отсутствия дополнительной информации значение интенсивности турбулентности можно задать равным 10%. Эту величину можно считать хорошим начальным приближением.

Таблица 2 – Граничные условия Flow Simulation

Для впускных и выпускных отверстий	Только для впускного отверстия
-    Масса и объем -    Объемный расход - Скорость - Число Маха - Статическое дав ление - Общее давление - Давление среды - Давление на стенке	-    Профиль скорости потока, линия завихрения или вектор -    Температура -    Состав (для сборок) -    Параметры турбулентности
Вентилятор	Теоретический вентилятор, который полностью определяется кривой, означающей группированную зависимость объемного расхода и перепада давления. Вентилятор можно использовать в качестве впускного и выпускного отверстий или внутреннего вентилятора. База данных содержит кривые вентилятора для выбранных промышленных вентиляторов. Кроме того, можно самостоятельно определить кривые вентилятора.
Теплоотвод	Теоретический вентилятор, совмещенный с теплоотводом. Flow Simulation определяет теплоотвод по кривой вентилятора и кривой жаропрочности.
Термоэлектрический охлаждающий модуль	Теоретическое охлаждающее устройство Peltier определяется по разнице максимальной температуры, которую оно может выработать.

В неопределенных случаях рекомендуется задавать интенсивность и турбулентной вязкости. В этом случае рекомендуемое значение для степени вязкости – 10. В таких потоках как, высокорейнольдсовые пограничные слои, сдвиговые слои, полностью развитое течение в каналах, степень турбулентной вязкости может находиться в диапазоне от 100 до 1000.

Наиболее полно учесть параметры турбулентности, в том числе и произвести выбор наиболее подходящей модели турбулентности и ее параметров позволяют не все доступные программные средства (например, такие как Ansys/Flotran, Comsol и др.).

В интерфейсе Flow Simulation представлено на выбор два способа выбора входных параметров: интенсивность турбулентности + масштаб длины и энергия турбулентности + скорость диссипации энергии турбулентности. Задание граничных условий во Flow Simulation можно производить через панель быстрого доступа (Insert Boundary Conditions). Достаточно в открывшемся окне Boundary Conditions выбрать поверхности как твердого тела, так и границ потока газов или жидкости, на которых задаётся граничное условие.

В качестве граничных условий (табл.2) на поверхностях твердого тела (Real wall) задают: температуру стенки т,Κ; коэффициент теплоотдачи а, (Вт/(м2 /К), шероховатость стенки ^z , мкм, либо выбирают (Ideal wall) – адиабатическая, гладкая стенка и задают только температуру стенки и шероховатость (либо тепловой поток Вт/м2).

Пример расчета теплообменника

В качестве примера приведем расчет теплообменника "труба в трубе" [8], выполненного более подробно в конструктивном исполнении (рис.3). Материал теплообменника – медь

На входной границе потока задаётся граничное условие типа «входной массовый (кг/с) или объемный (м 3 /с ) расход» (inlet mass flow) либо скорость потока (м/с ), его конфигурация, а также температура (К) и давление (Па). На выходной границе задаётся начальное приближение типа «давление окружения» (environment pressure) и температура, либо определяются параметры потока соответствующие входным и условиям задачи.

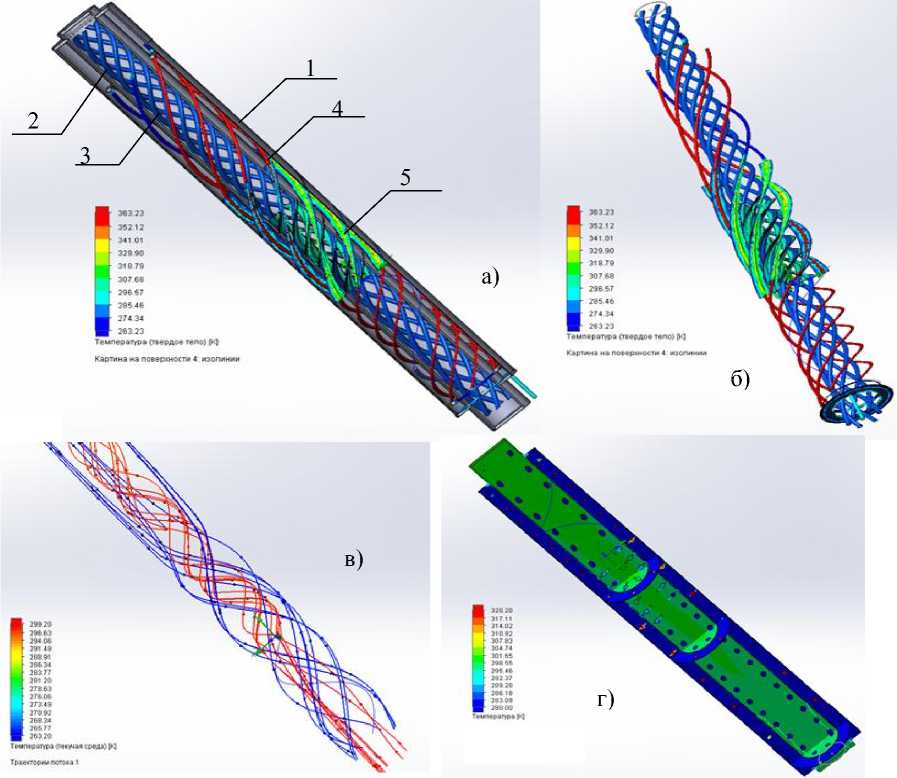
Рисунок 3 – Результаты расчетного анализа теплообменного устройства : а) – конструкция теплообменного аппарата: 1 – внешняя труба; 2 – внутренняя труба; 3, 4 – тепловые трубки; 5 – турбулизатор; б) – распределение температуры по поверхности тепловых трубок; в) – траектории потока (температура текучей среды); г) – распределение температуры по сечению аппарата

Условиями задачи предусмотрен теплообмен с окружающей средой и радиационный обмен с тепловыми трубками, размещенными во внутренней и внешней трубах. Внутренняя тепловая трубка имеет температуру 276,2 К, а внешняя 363,2 К, соответствующие температурам проходящего по ним теплоносителя. По трубам движется воздух, омывающий тепловые трубки, и имеющий температуру 263К и 299 К, соответствующие температурам внешней среды и вентилируемого воздуха На первом этапе расчета проводилась оценка влияния параметров - модели турбулентности путем изменения параметров модели для входящего и выходящего потоков воздуха в широком диапазоне:

• -    по I _t — L_t варианту I_t= 5 ^ 100%;

L _t=0,0001 ^ 0,1 m;

по к — £ варианту к= 1^100J/kg(Дж/кг); е=1 ^ 100 W/kg (Вт/кг).При этом результаты расчета (рис. 3) оказались идентичными, что характеризует отсутствие существенного влияния турбулентности во входящем потоке на обтекание поверхностей теплообменника. Результаты расчета, проведенные исходя из ламинарных режимов обтекания, также получились идентичными предыдущим.

На втором этапе расчет проводился с учетом изменения конструкции теплообменного устройства путем установки пластинчатых винтовых лопастей, закручивающих поток в центральной части теплообменного устройства. В результате расчетов получено, что установка таких лопастей увеличивает теплоотдачу за счет изменения скорости обтекания труб на 16,7 % в целом.

Исследование теплоотдачи в тепловой пушке

Эффективность интенсификации процесса теплопередачи далее рассмотрим на примере тепловой пушки (рис. 4). Здесь закрутка потока воздуха производится путем установки винтовых лопастей во входном сечении фена.

а)

^7/ш

б)

в)

г)

д)

е)

Рисунок 4 - Интенсификация рабочего процесса тепловой пушки: а) - конструкция: 1 - корпус;

2 - спираль; б) - д) - температура в потоке с различной закруткой;

е) - распределение скорости в закрученном потоке

Результаты расчетов показывают очевидную зависимость температуры потока на выходе от интенсивности закрутки потока.

Очевидно, что увеличение интенсивности закрутки потока, с одной стороны, приводит к увеличению местной скорости, омывающего нагревательный элемент потока (в полтора раза от средней), а с другой – увеличивает путь, на котором происходит взаимодействие частиц потока с нагретой поверхностью. Оба этих фактора способствуют увеличению теплоотдачи от нагреваемого элемента. Температура потока за нагреваемым элементом увеличива- ется при увеличении интенсивности закрутки потока. Следует отметить также, что снижение скорости входного потока также приводит к увеличению температуры на выходе. Однако в этом случае мощность теплоотдачи уменьшается

Рисунок 5 – Теплообменник теплового насоса: а) – внешний вид; б) – картина от тепловизора (коэффициент излучения: 0,94; отраж. темп. 27,0°С; самая холодная точка – + 25,1°С; самая теплая точка – +31,3°С )

Для исследования работы теплового насоса использовались тепловизор и мультиметр, которыми были измерены электрические и термодинамические параметры. В частности, были получены следующие данные: t вх =24°С – температура на входе в теплообменник (она же температура наружного воздуха); t _вых=20°С – температура воздуха, выходящего из теплообменника; p =680 Вт – мощность потребления электроэнергии при работе мотора компрессора. Температурное поле, полученное с помощью тепловизора, представлено на рис. 5 б).

Внешний теплообменник теплового насоса представляет собой изогнутую оребренную трубку, по которой протекает газообразный (кипящий при низкой температуре ( -25 – -

Проектирование теплообменника теплового насоса

Полученные при анализе теплообменных устройств данные об интенсификации процесса теплообмена были положены в основу проектирования внешнего теплообменника теплового насоса "Воздух – Вода". В качестве прототипа был выбран теплообменник теплового насоса AVH-12V1D (рис.5).

Источником низкопотенциальной энергии для теплового насоса является наружный воздух, который вентилятором направляется во внешний блок и к контуру хладагента. Хладагент нагревается, забирая теплоту от воздуха, и далее поступает в компрессор, где сжимается и поступает уже с высокой температурой в теплообменник внутреннего блока. Там тепло отдается теплоносителю – воде, которая далее следует в радиатор и отапливает помещение. Эффективность работы теплового насоса в большой мере зависит от эффективности рабо- ты теплообменных устройств и, в частности, от испарителя, размещенного во внешнем блоке теплового насоса (рис.5).

15°С) хладагент. Основным недостатком такой (сетчатой) конструкции является ее низкая проницаемость для воздушного потока. Это приводит к необходимости установки относительно мощного вентилятора, побуждающего поток к движению через конденсатор.

Для совершенствования теплообменника теплового насоса предлагается конструкция (рис.6), представляющая собой концентрично расположенные винтовые пластины 3, скрепленные с трубками 2, заполненными хладагентом. Вся конструкция размещена в трубчатом корпусе 1 и разделена по окружности концен-трично расположенными теплопроводящими перегородками 4.

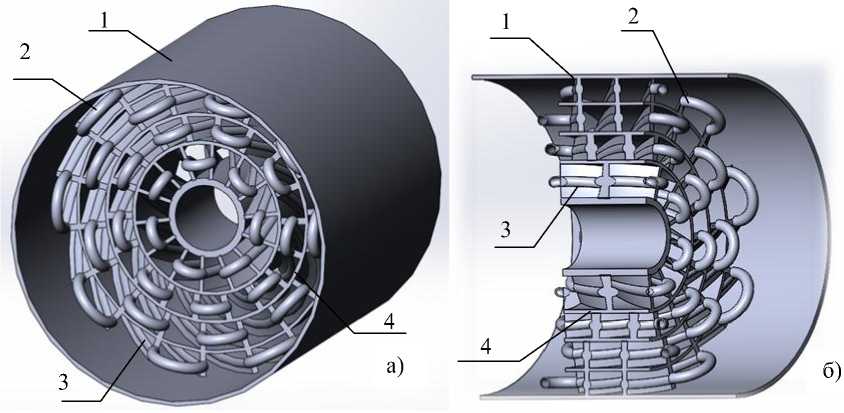
Рисунок 6 – Конструкция ротационного теплообменника: а) – внешний вид проточной части; б) – разрез: 1 – внешний корпус; 2 – трубки с хладагентом; 3 – винтовые пластины; 4 – перегородки из теплопроводящего материала

В качестве граничных условий задан входящий ламинарный поток воздуха с температурой t _вх=20°С и выход в невозмущенную атмосферу с той же температурой и нормальным давлением. Для анализа выходного потока и соблюдения граничных условий расчетная область расширена специальной цилиндрической насадкой на поверхности которой и заданы граничные условия.

Результаты полученных расчетов интерпретированы картинами постпроцессора SolidWorks/Flow Simulation (рис. 7- 9).

Анализ представленных на рис 6 – 8 картин показывает, что в результате вынужденного протекания воздуха через теплообменник формируется поток, температура которого ниже температуры окружающего воздуха. Распределение температуры неравномерное, так что в центральной части потока температура на несколько градусов ниже температуры окружающей среды. При удалении от центра к периферии потока температура приближается к температуре окружающей среды. При этом формируется четкая граница потока, имеющая значительный градиент температуры.

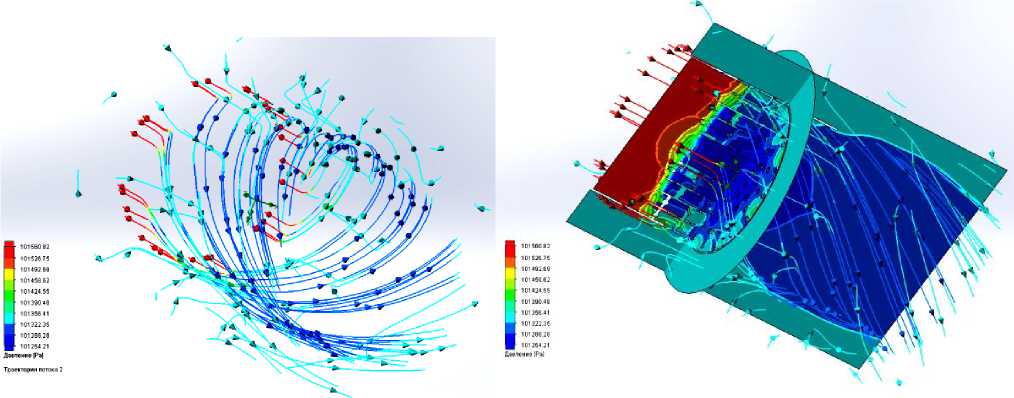
Рисунок 7 – Картины распределения давления в потоке

Рисунок 9 – Скорости линий потока

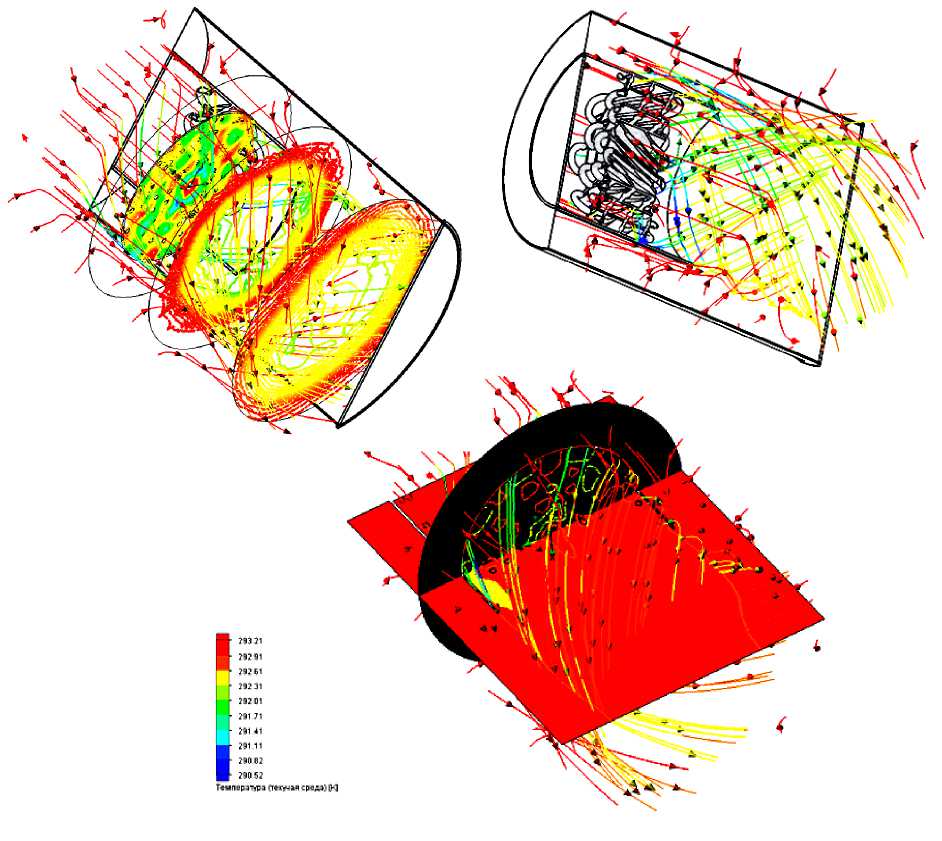
Рисунок 8 – Картины распределения температуры воздуха в потоке

Практически по сечению выходного потока его температура постоянная (за исключением границы и, в некоторых случаях, обусловленных малой скоростью потока, небольшой зоны по самому его центру). По мере удаления от выходного сечения поток постепенно расширяется, так что на расстоянии двух диаметров его площадь увеличи- вается примерно всего на 60%, а границы расширяются за счет диссипации температуры по поперечному сечению. У фронта теплообменника формируется зона повышенного давления (рис.7), а у тыльной части – пониженного. Скорость частиц воздуха в потоке (рис.9) увеличивается на участке закручивания лопастями (здесь она наибольшая) и остается большей поступательной составляющей на выходе из теплообменника.

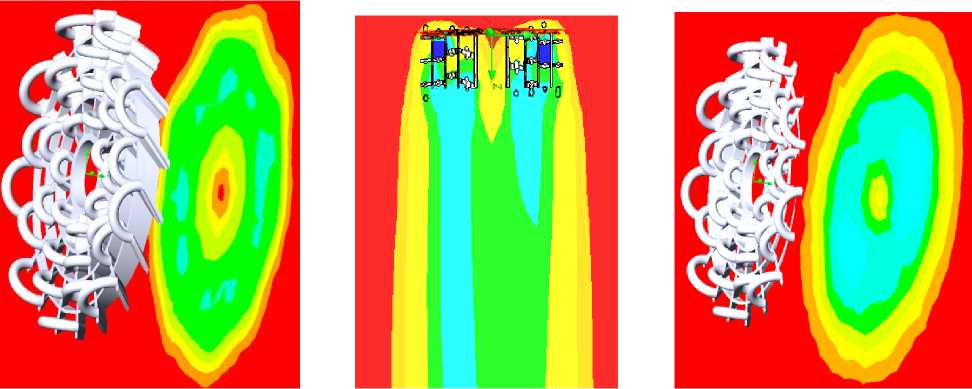
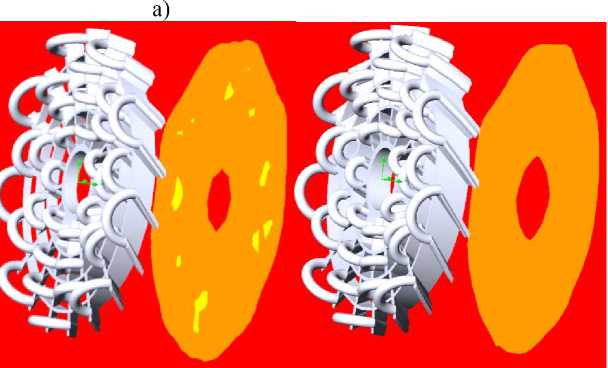
Для оценки количественного влияния расхода вентилируемого через теплообменник воздуха на его теплофизические и аэродинамические свойства поставлена и решена средствами SolidWorks/ Flow Simulation внешняя задача обтекания рабочей части теплообменного устройства (рис.5) воздухом, с температурой +20 °C с различными скоростями. Результаты представлены в виде картин распределения температуры и давления на рис. 10 и 11 , соответственно. Полученные результаты позволили получить значения теплофизических и аэродинамических характеристик теплообменного устройства, представленные в табл.2.

б)

в)

293.2В

290.92

• -    288.58

• -    286.24

• -    283.90

• -    281.56

• -    279.22

1 276.88 274.54 272.20

Температура (текучая среда) [К]

г)                        д)

Рисунок 10 – Картины распределения температуры воздуха в потоке при различных скоростях :

• а) – и = 1 м/c; б) – и = 3 м/c; в) – и = 5 м/c; г) – и = 10 м/c; д) – шкала температуры

  

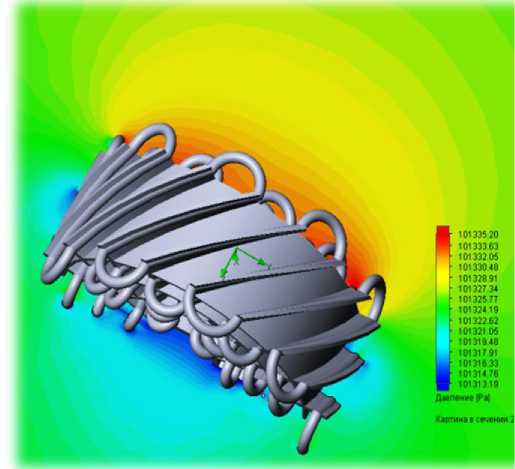
  Рисунок 11 – Картина распределения давления в потоке ( и = 5 м/c)

  
  

Q =         ср - 293,2) ;

2 Δ р =, ²

где:   Ср – теплоемкость воздуха

=

1005 Дж/(кг К);  р – плотность воздуха, р = 1,205 кг/м3.

Результаты таблицы 2 интерпретированы графиками на рис. 12 – 14.

Из результатов, представленных графиками на рис. 12 – 14, следует, что тепловая мощность спроектированного теплообменного устройства растет с увеличением скорости вентиляции проточного воздуха до значений 3 – 5 м/с, а затем постепенно снижается по мере увеличения скорости до 10 м/с. При этом температура выходного потока воздуха также увеличи- вается и при скорости, равной и ≅ 10 м/c приближается к температуре окружающей среды. По мере увеличения скорости обдува увеличивается также во второй степени аэродинамическое сопротивление теплообменника, что потребует увеличение мощности вентилятора, побуждающего воздух к вентиляции через теплообменник. Следовательно, для данной конструкции теплообменного устройства оптимальной скоростью обдува воздуха будет являться величина u , находящаяся в пределах 3 – 5 м/с.

Таблица 2 – Теплофизические и аэродинамические характеристики теплообменника

№ оп	Скорость потока, м/с	Расход воздуха, G , м3/с	Средняя температура выходного потока, I ср , К	Тепловая мощность, Q , КВт	Избыточное давление, Δ p , Па	Коэффициент сопротивления Cz
1.	1	0,0683	277	1,34	0,85	1,41
2.	3	0,205	282	2,78	8	1,48
3.	5	0,342	286	2,98	23	1,53
4.	7	0,479	285	2,76	52	1,76
5.	10	0,686	290	2,66	206	3,42

Температура выходного                         Тепловая мощность, КВт

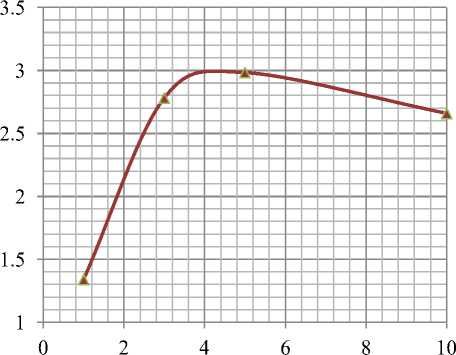
Скорость, м/с

Рисунок 12 – Изменение тепловой мощности от скорости

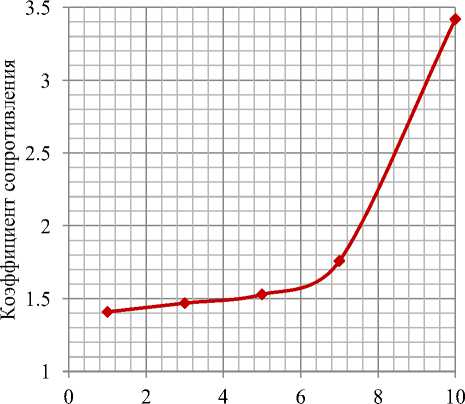
Скорость, м/с

Рисунок 14 – Изменение аэродинамического сопротивления от скорости

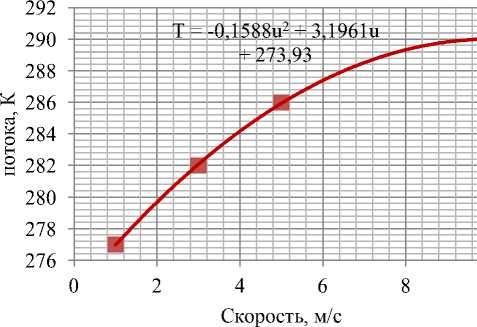
Рисунок 13 – Изменение температуры выходного потока от скорости

Наличие оптимальной скорости обдува наглядно иллюстрирует график, представленный на рисунке 14. Здесь характер изменения аэродинамического сопротивления, рассчитанного в соответствии с формулой (36) иллюстрирует переход характера обтекания сложных поверхностей теплообменника в диапазоне скоростей 5 – 10 м/с. Это приводит к практически скачкообразному увеличению аэродинамического сопротивления. Эффективность теплообменного процесса при этом снижается.

Выводы

Рабочие процессы, протекающие в теплообменных аппаратах, характеризуются сложным в большой степени нестационарным течением теплоносителя, связанным и зависящим от геометрических характеристик проточной части теплообменного аппарата, а также с особенностями его компоновки и устройства. При этом интенсификация гидрогазодинамического процесса посредством механического воздействия на воздушный поток, обеспечивающая его вращение приводит к значительному повышению интенсивности теплообмена при снижении аэродинамическое сопротивления.

Проведенные в статье исследования различных по конструкции и назначению теплообменных устройств показали эффективность современных вычислительных средств и САD/CAE технологий для их проектирования и определения оптимальных режимов их функционирования.

Разработанные в статье конструкции теплообменных аппаратов и их обоснованные параметры могут быть использованы в практике проектирования и обоснования параметров подобных по назначению устройств.