Повышение энергетических показателей работы асинхронных электроприводов с центробежными агрегатами

Весомая часть электрической энергии в агропромышленном комплексе потребляется электрическими двигателями. Это электропривод насосных, компрессорных, вентиляционных, разных видов транспортных, зерноперерабатывающих и других установок.

Одним из массовых потребителей всей электрической энергии (около 30%) является электропривод центробежных механизмов: насосов, вентиляторов, компрессоров и т.д. – с обязательным регулированием производительности. Простым в реализации является способ регулирования с помощью задвижек, вентилей, клапанов – путем введения их в нагнетающую магистраль, но весьма не экономичным, так как при этом изменение характеристик расход-давление трубопровода (магистрали) достигается за счет возрастания потерь в системе, а не за счет уменьшения мощности центробежного механизма. Наиболее перспективным регулированием производительности является электрический способ, т.е. изменение скорости вращения асинхронного двигателя в энергосберегающем режиме. При таком переходе экономический эффект появляется за счет улучшения эксплуатационных характеристик технологического оборудования и обеспечивает снижение в среднем на 20–30% расхода электроэнергии, потребляемой электроприводами.

Технически это реализуется включением между сетью и двигателем управляемого электрического преобразователя, воздействующего на скорость вращения двигателя, благодаря чему исключается необходимость использования других энергетических регулирующих средств.

Р мех = M • * (1)

В качестве электрических преобразователей применяют тиристорные регуляторы напряжения (ТРН) и преобразователи частоты (ПЧ).

Постоянство частоты тока статора предполагает регулирование только напряжения статора АД с помощью ТРН. Это упрощает также поиск условий, обеспечивающих минимизацию потерь. Рассмотрим это на примере АД типа 4А80В2У3 Р н = 2,2 кВт , n ₀ = 3000 об / мин .

Рассматривая существующие возможности для решения этой задачи, делаем вывод, что путем регулирования напряжения можно обеспечить минимум потерь мощности, минимум тока статора и активной мощности [1]. В настоящее время предложены различные системы автоматического регулирования, обеспечивающие минимизацию одной из этих величин.

Нами предлагается один из способов энергетической оптимизации асинхронного электропривода – минимизация потерь.

Для обеспечения минимума потерь мощности необходимо поддерживать определенное скольжение.

Скольжение sопт , соответствующее минимуму потерь, находится из выражения dДР

ds

= ^Mc • ® 1 н

C

• с1 • s + —+ (1 + kcm )• с3 • s + —

к

s

к

= 0

,

где

с = ¹⁺^ ^{1 +}

r

к

( X s

л2 Л

Y к © 7

,

C 2 =

Г 1

\2

У к ^ 7

• R s • R r ,

с ₃ = с 3

•

ДР

ст . н

с 4

,

С = ^с 3

Д Р  X © r

♦

M c • ч • (1 + k ст ) • с ; • s ’ +—

3 • E, ² R © _r ’

к

s’

с 4 = с 4

•

А Р ст . н

с

^4

,

C 4 =

M c • % • (1 + к ст ) • C ; • s ’ + —

Д Р

—г • R ©r, 3 • E ² r

ст , н

н

к

s’

^{Д Р}м , н ,    Д Р м,н = M н • ч н

• с • s к

Q I ' н ⁺ l , ^sн 7

^{Д Р}н = P H -⁽¹ - П н )/ П н ,

где к_ст - коэффициент потерь в стали (принимается равным 0,5); А Р_н , Д Р_ст , _н , Д Р м , _н - полные потери, потери в стали, потери в меди двигателя в номинальном режиме; s_н – номинальное скольжение, Е_н – ЭДС фазы двигателя в номинальном режиме, I_н , M_н – номинальный ток, момент двигателя; R_r, R_s , X_s , X'_r, X _A - параметры схемы замещения. Первое и второе слагаемые в скобках (2) определяют мощность потерь в меди двигателя, третье и четвертое – мощность потерь в стали.

Продифференцировав выражение (2), получим уравнение пятого порядка с коэффициентами к 1, k 2, к3, k4, к5 которое решается численным методом при помощи MATLAB , k1 • s5 — к2 • s4 + к3 • s3 — к4 • s2 + к5 = 0,

где к 1 , к ₂, к 3 , к ₄, к ₅ - коэффициенты для выбранного АД; к - показатель степени.

_к = ( M с.н — M о ) _;

1,5 • с 4 ) ;   (13)

(1 — s^ )2 ’ к1 = 2 • к • (с1 +1,5 • с3);

к ₂ = 5 • к • ( с ₁ + 1,5 • с 3 ) ;

к ₃ = 2 • [ к • ( с , + с ₂ + 1,5 • с 3 + 1,5 • с 4 ) + к • ( с , + 1,5 • с 3 )] ;

к4 = 4 • к • (с2 +1,5 • с4) + M0 • (с1 +1,5 • с3) + к • (с1 — с2 +1,5 • с3 — k5 = (k + M 0) • (C2 +1,5 • C4) ,

где M ₀ – начальный момент сопротивления механизма, не зависящий от скорости вращения ( M 0 « 0,15 • M _fa ) - пятнадцать процентов от номинального момента), Н м; M сн = Р сн / ю сн - момент сопротивления механизма при номинальной скорости вращения.

Анализируя выражение (8), можно сделать следующий вывод: коэффициенты k ₁ , k ₂ , k ₃ малы, а

C ₂ » 0 , C 3 « 0 , тогда оптимальное скольжение определится

S опт

1,5 • C 4 • ( k + M 0 )

У M 0 • C 1 + k • ( C 1 + 4,5 • C 4 )

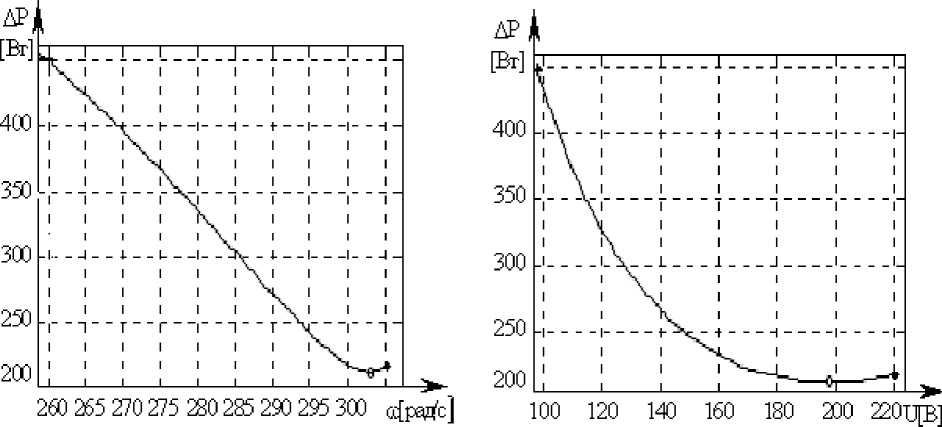
На рисунке 1 (а, б) показаны рассчитанные зависимости потерь от напряжения и угловой скорости вращения асинхронного двигателя типа 4А80В2У3 (2,2 кВт, 3000 об/мин) при вентиляторном моменте на валу.

а                                  б

Рис.1. Зависимости мощности потерь в асинхронном двигателе 4А80В2У3 от угловой частоты вращения (а) и от напряжения (б), где *,о,+ - потери мощности при номинальном, оптимальном и минимальном напряжении АД

Проведенный анализ рисунка 1 позволяет сделать вывод: для обеспечения минимальных потерь в двигателе необходимо при любых нагрузках поддерживать постоянное оптимальное скольжение, определяемое выражением (15). Это свойство асинхронного двигателя позволяет обеспечить минимизацию потерь в системе автоматического регулирования с обратной связью, где за счет стабилизации скорости автоматически изменяется напряжение статора двигателя в функции момента на валу по закону

^Y опт

^Mопт • ( s ^{2 + S}Lt + ² • a • s K • ^Sonm )

\    ² • ^Mк ■ s K • s onm • ^{(1 +} a • s K )

Оптимальная точка относительно минимума потерь для рассматриваемого АД имеет параметры: Д Р опт = 206,7 Вт , U опт = 192 В при Y _onm = 0,87 .

Помимо регулирования скорости вращения с помощью ТРН, который можно использовать для относительно небольшого диапазона регулирования, возможно применения частотного способа для более глубокого регулирования. Принцип данного метода заключается в том, что изменяя частоту f1 питающего АД напряжения, можно в соответствии с выражением угловой частоты вращения магнитного поля статора изменять его скорость, получая при этом искусственные характеристики

^ 0 = ² • ^п • ^fJp . ⁽¹⁷⁾

При регулировании частоты возникает также необходимость регулирования амплитуды напряжения источника, что следует из выражения

U ₁ « E 1 = k -Ф- f. . (18)

Из приведенного выражения (18) следует, что если при неизменном напряжении источника питания U ₁ изменять частоту, то магнитный поток асинхронного двигателя будет изменяться обратно пропорционально частоте. Так, при уменьшении частоты поток возрастает и это приводит к насыщению стали двигателя и, как следствие, к резкому увеличении тока намагничивания и превышению температуры двигателя; при увеличение частоты f ₁ поток будет уменьшаться и, как следствие, будет уменьшаться допустимый момент.

Для наилучшего использования АД и получения высоких энергетических показателей его работы – коэффициентов мощности, полезного действия, перегрузочной способности – необходимо регулировать напряжение одновременно в функции частоты и нагрузки, что реализуемо только в замкнутых системах электропривода. В разомкнутых системах напряжение регулируется лишь в функции частоты по закону, зависящему от вида нагрузки.

Изменение частоты источника питания позволяет регулировать скорость асинхронного двигателя как выше, так и ниже основной. Обычно при регулировании выше основной скорости частота источника питания превышает номинальную не более чем в 1,5–2 раза. Указанное ограничение обусловлено прежде всего прочностью крепления обмотки ротора. Кроме того, с ростом частоты питания заметно увеличиваются величины потерь мощности, связанные с потерями в стали статора. Регулирование скорости вниз от основной, как правило, осуществляется в диапазоне до 10–15.

Частотное регулирование угловой скорости является экономичным, так как управление двигателем производится при малых скольженьях. Кроме того, при частотном управлении, так же как и при ТРН, достигается минимум потерь в АД или минимум потребляемого двигателем тока или экстремума других энергетических показателей.

Для частотного способа управления на примере асинхронного двигателя 4А80В2У3 ( Р_н = 2,2 кВт ) при вентиляторном моменте на валу потери мощности определяются значением абсолютного скольжения в . С другой стороны, сам режим на валу является функцией управляющих воздействий на двигатель (напряжения или тока и частоты). Закон управления двигателем, обеспечивающим минимум потерь при вентиляторном моменте на валу, определяет величину напряжения (тока), при котором значение абсолютного скольжения в соответствует минимуму потерь мощности [2]

d A P в

= M c • ^Ь 1

• - • в + — + а

{ ¹ в

Л

■ ( 1 + акс )| C з • в + -j J

где а = в + Ь;

Ь - относительная скорость при ® _min и a max .

Продифференцировав выражение относительно в , получим уравнение четвертого порядка, которое решается численным методом при помощи MATLAB. Зависимости оптимального абсолютного скольжения и относительной частоты от угловой скорости вращения представлены на рисунке 2.

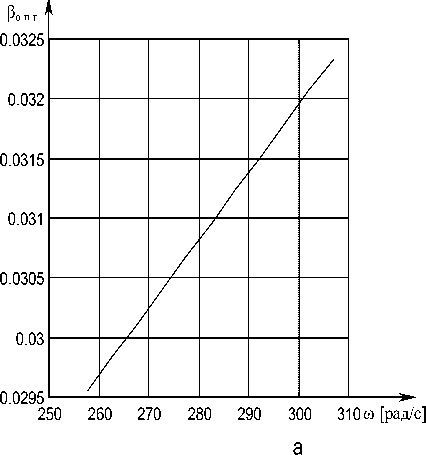
Рис.2. Зависимость оптимального абсолютного скольжения (а) и оптимальной относительной частоты

(б) от угловой скорости вращения

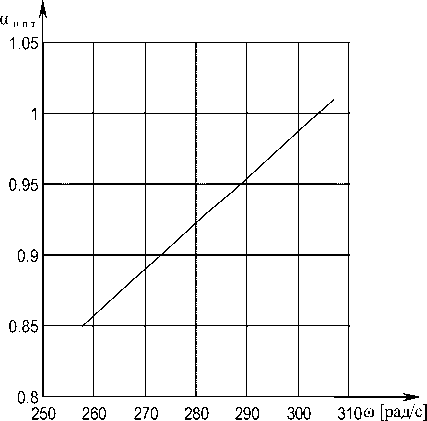
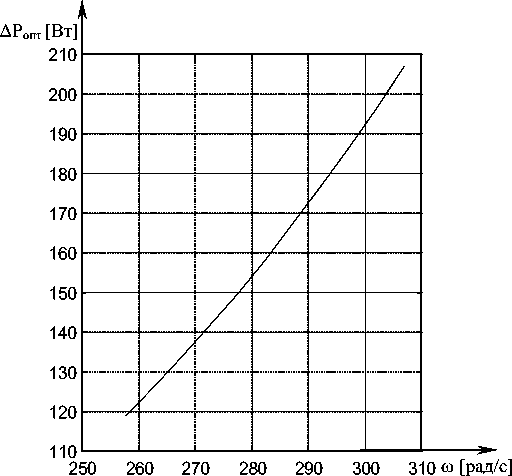
Рис.3. Зависимость оптимальных потерь мощности от угловой скорости вращения A P onm = f( & ) (от © min до © max )

При уменьшении угловой скорости вращения (рис. 2) оптимальная относительная частота α и оптимальное абсолютное скольжение в режиме минимума потерь уменьшается.

Оптимальные потери мощности при оптимальном абсолютном скольжении и оптимальной относительной частоте представлены на рисунке 3, Из которого видно, что потери в двигателе при управлении по минимуму потерь в зависимости от угловой скорости вращения – уменьшаются.

Потери мощности при угловых скоростях © _min , © max от абсолютного скольжения и от относительной частоты представлены на рисунке 4.

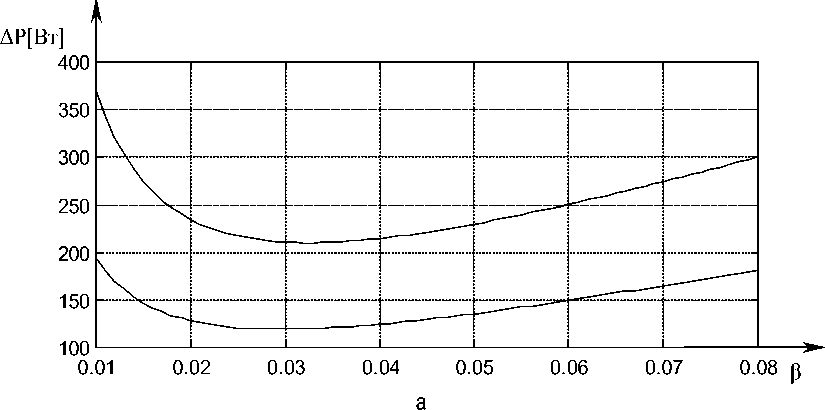
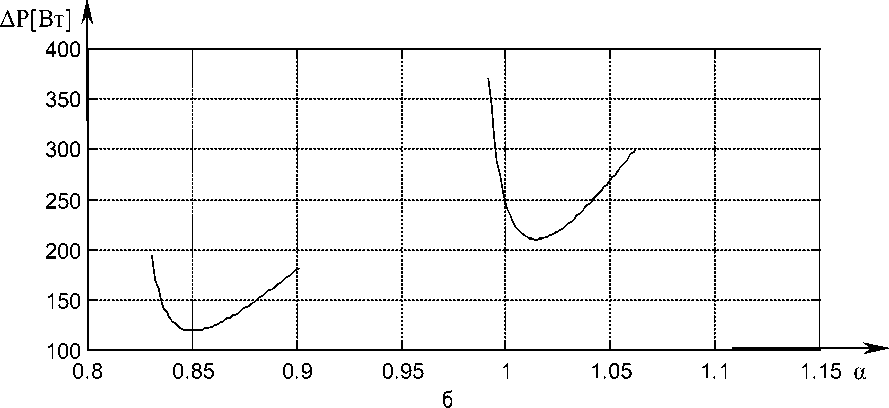
Рис.4. Зависимость абсолютного скольжения (а) и относительной частоты (б) от потерь мощности

Из выражения (19) и рисунка 4 видно, что при каждой угловой скорости из интервала (от ω _min до ω _max ) существует оптимальное абсолютное скольжение и оптимальная относительная частота.

Проведенные исследования показали, что тиристорное и частотное управление позволяют регулировать скорость вращения и обеспечивать энергосберегающие режимы работы автоматизированного электропривода (АЭП) с центробежными механизмами. Режим энергосбережения позволяет минимизировать потери мощности. Сущность такого управления в установившемся режиме состоит в поддержании некоторого постоянного оптимального скольжения, соответствующего минимуму потерь. Практически это достигается в системах автоматического регулирования с обратной связью по скольжению (или скорости).

При тиристорном управлении оптимальное значение скольжения (15) почти не зависит от C ₂ ≈ 0 , C ₃ ≈ 0 , определяющих мощность потерь в меди ротора и в стали статора двигателя.

Исследования показали, что частотное управление позволяет оптимизировать потери мощности для АЭП с центробежными агрегатами путем поддержания оптимального абсолютного скольжения, определяемого электрическими параметрами двигателя и относительной частотой. При таком управлении для каждой скорости ЭП существует такое соотношение β и α , которое даст минимум потерь мощности.

Частотное регулирование угловой скорости – плавное, бесступенчатое, с минимальными потерями в асинхронном двигателе по сравнению с тиристорным способом регулирования. Но оно требует применения относительно сложного и дорогостоящего преобразователя частоты.