Повышение энергоэффективности систем радиосвязи с ортогональным частотным мультиплексированием сигналов на основе их экстраполяции по Калману
Автор: Воронков Григорий Сергеевич, Кузнецов Игорь Васильевич, Султанов Альберт Ханович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии радиосвязи, радиовещания и телевидения
Статья в выпуске: 3 т.15, 2017 года.
Бесплатный доступ
В статье рассмотрен вопрос энергоэффективности систем подвижной радиосвязи. Предложен метод ее повышения на основе дифференциального преобразования сигналов систем, использующих ортогональное частотное мультиплексирование, с использованием экстраполяции сигналов. Сформулированы требования к экстраполятору, предложена структурная схема формирования и приёма сигналов, реализующая указанный метод. Показано, что в качестве экстраполятора может быть использован фильтр Калмана, представлена математическая формулировка задачи его синтеза. Получено решение дифференциального уравнения фильтра Калмана для сигналов синфазного и квадратурного каналов для случая синхронной работы системы. Показана ортогональность разностных сигналов. Получено условие устойчивости системы восстановления сигналов, показано, что условие выполняется для полученного решения. Продемонстрировано повышение энергоэффективности системы HSPA+ при использовании предложенного метода. На примере усилителей производства компании Analog Devices показано, что использование предложенного метода позволяет снизить мощность, потребляемую оконечным усилительным каналом передатчика, что позволяет увеличить время автономной работы систем беспроводной связи.
Дифференциальное преобразование сигналов, экстраполяция сигналов, фильтр калмана, повышение энергоэффективности, уменьшение динамического диапазона, системы беспроводной связи ofdm
Короткий адрес: https://sciup.org/140255672
IDR: 140255672 | УДК: 621.396 | DOI: 10.18469/ikt.2017.15.3.10
Текст научной статьи Повышение энергоэффективности систем радиосвязи с ортогональным частотным мультиплексированием сигналов на основе их экстраполяции по Калману
Увеличение скорости передачи сигнала в беспроводных системах ведет к необходимости использования спектрально-эффективных видов модуляции [1]. Подавляющее большинство существующих и перспективных стандартов беспроводной связи (WiFi 802.11g и выше, 3GPP LTE, LTE-Advanced, 5G, спутниковых коммуникаций) используют для повышения спектральной эффективности технологию ортогонального частотного мультиплексирования (OFDM) [2-3]. При этом ужесточаются требования к отношению «сигнал-шум» на приеме [2]. Для обеспечения помехоустойчивости каналов необходимо увеличивать мощность передатчика. Однако увеличение мощности передатчика негативно сказывается на энергопотреблении устройств связи, поскольку в современных системах радиосвязи до 70% мощности затрачивается на передачу сигналов (их оконечное усиление). Следовательно, снижение энергопотребления (повышение энергоэффективности) является актуальной задачей.
В настоящее время решение данной задачи в основном осуществляется прямыми методами управления мощностью передатчиков [2], что требует организации каналов обратной связи между узлами сети, увеличивает время регулирования мощности и т.д. Перспективным методом является применения новых видов модуляции, например поворота сигнального созвездия в си- стемах с квадратурной модуляцией [4], однако это решение требует изменений в схемотехнике и алгоритмах функционирования передающих устройств, что подразумевает замену трансиверов эксплуатируемых систем, что ведет к увеличению затрат на модернизацию систем.
Косвенным методом понижения энергопотребления является уменьшение скорости передачи данных, обеспечиваемое методами сжатия информации. Недостатком этих методов является повышение вычислительной сложности, особенно для многоканальных систем. Приведенные выше недостатки можно преодолеть применением дифференциального преобразования [5-7]. Такое решение уменьшает динамический диапазон канального сигнала, что позволяет использовать для передачи усилители радиочастоты с меньшей выходной мощностью в режимах, обеспечивающих максимальный коэффициент полезного действия.
Таким образом, дальнейшая задача состоит в разработке схемы дифференциального преобразования сигналов для систем, использующих ортогональное частотное мультиплексирование, и синтезе ее параметров.
Постановка задачи
Вначале опишем структуру системы связи, использующей дифференциальное преобразование, приведенную на рис . 1. Структура тракта передачи
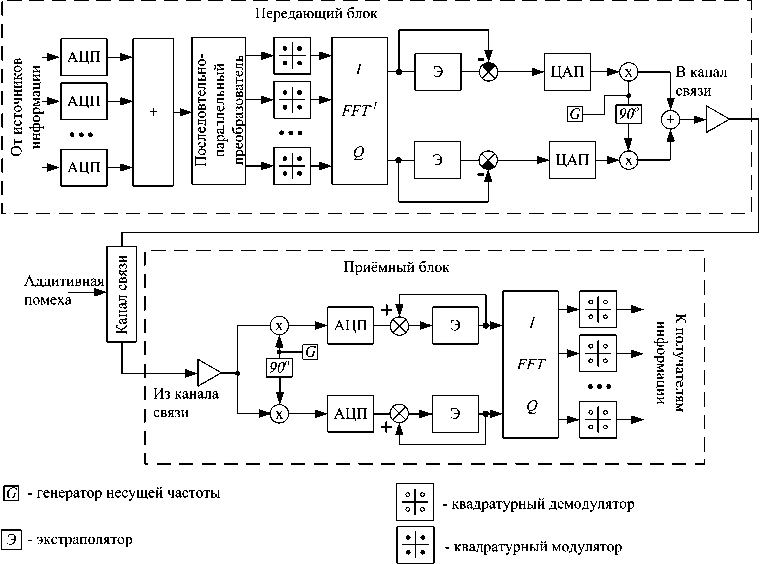
Рис. 1. Структура формирования и приема сигнала OFDM при использовании экстраполяции по входу
и приёма сигнала OFDM дополнена устанавливаемыми в синфазном и квадратурном каналах экстра-поляторами. На блок высокочастотного модулятора при этом подаётся разница экстраполированного и текущего значений комплексной огибающей. После прохождения по каналу связи (примем канал с аддитивным белым гауссовским шумом) сигнал демоду-лируется, вновь проходит через блок экстраполятора и суммируется с экстраполированным значением. При этом предполагается, что параметры экстрапо-лятора на приеме известны. Далее восстановленная комплексная.
Таким образом, экстраполятор должен удовлетворять следующим требованиям:
– уменьшение динамического диапазона сигналов с учетом уровня действующей помехи при сохранении параметров канала (скорости передачи, вероятности битовой ошибки);
– сохранение ортогональности по Гильберту сигналов синфазного и квадратурного каналов (ортогональность разностных сигналов синфазной и квадратурной составляющей);
– сохранение устойчивости приёмного блока ввиду наличия положительной обратной связи.
Математическая постановка задач построения экстраполятора может быть сформулирована следующим образом. При известной форме входных сигналов Х[(0 и Хо(0 и известной форме помехи и (?), имеющей спектральную плотность мощности (СПМ) No, найти оценки входных сигналов £Д0 И XqV) , обеспечивающие минимум динамических диапазонов разностных сигналов eAt) и eQ(t) и сохраняющие при этом их ортогональность:
к, (?) = м[е; (?)] = М ^х, (t) - Xj (?))" ]—> min;
kQ (0 = M[eJ (?)] = М (хе (?) - xQ (О)2 ]~> min;
е7 (?) = х, (t)-ij(ty,eQ (?) = xQ (t) - kQ (t);
^ /м(е7(т) eQ(t-r))dT = O, где T – период наблюдения.
Решение
Решение будем искать для синфазного канала (канала I ). Покажем, что указанным выше требованиям может соответствовать экстра-полятор на основе фильтра Калмана-Бьюси. Предположим, что спектральную плотность мощности (СПМ) ХД®) исходного сигнала можно представить в виде куполообразной функции [8]:
х,И =
2 a Pj a2 + co2 ’
где PI – мощность сигнала; ex – параметр фильтра Калмана, определяющий крутизну СПМ сигнала; co – нормированная угловая частота.
Структурная схема фильтра Калмана для такого случая приведена на рис. 2. Представленная схема характерна тем, что непосредственно в фильтре учитывается весь процесс передачи и приема сигнала. Генератор Г и пе-ремножители выполняют роль высокочастотных модулятора и демодулятора. Сигнал n ( t ) – действующая в канале передачи помеха с СПМ N 0, которая, в свою очередь, определяет передаточную функцию приемного предусилителя ki (No). Охваченный отрицательной обратной связью интегратор реализует уравнение фильтра Калмана [8-9]. При прохождении сигнала синфазного канала через фильтр Калмана получаем оценку сигнала (его экстраполированное значение), которое сравнивается (элемент сравнения представляет собой разностный блок) с исходным значением сигнала, таким образом, после сравнения в системе в качестве информационного используется уже разностный сигнал.
В соответствии с рис. 2 запишем уравнения фильтра Калмана [8]:
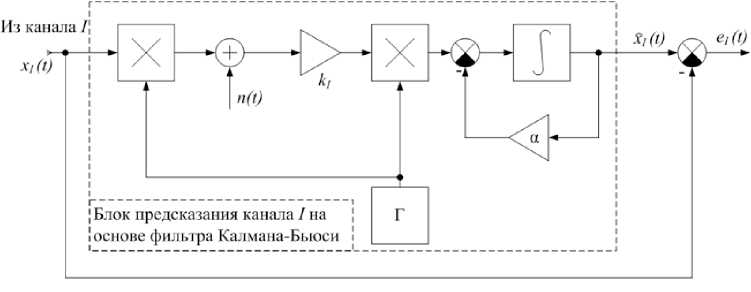
Рис. 2. Структурная схема экстраполятора синфазного канала «Infokommunikacionnye tehnologii» 2017, Vol. 15, No. 3, рр. 273-280
Эх АЙ 2k, (t )
—-— = —осх, (t) ч---—-cos( 8k,(t) Nu 2 kAO i, x —'— = —^ - 2ak, (?)--^——-cos” ((У?), 0t 2 1 No где z, (?) = X, (?) cos( Предположим, что 8kM = 0 . Тогда уравне-dt ние (1) сводится к квадратному уравнению относительно ^/ (0 , и его решение имеет вид: 8k AO 8t a1 Lф2р(с+?)У 2ЛЦ I No В установившемся режиме при ? ^ co получим lim^O=0. Таким образом, в установив-^” St шемся режиме сделанное предположение является правомерным и, следовательно, выражение (2) может быть использовано для синтеза передаточной функции фильтра Калмана в синфазном и квадратурном каналах. Произведем оценку выигрыша G в мощности сигнала для синфазного канала: G;=101g eAO A (0 = 201gf^4) Vх A0 к i (0i,2 2a+ 4c?2-4cos2(cot) ---COS (ГУ?) No Оценим отдельно числитель и знаменатель функций, стоящих под знаком логарифма. Для этого рассмотрим их поведение в установившемся режиме (при ? ^ CO ) и воспользуемся предельными тауберовыми теоремами: В соответствии с поставленной задачей будем рассматривать меньшее решение. При синхронной работе системы (синхронизации приемника и передатчика) принятие решения относительно оценки принятого сигнала будет происходить в дискретные моменты времени ?p , кратные периоду несущей: ? =2k / co. Тогда значение к i (0 можно записать в упрощенной форме: kAO = — 2a- 4a2 -4^ 7 4 ( \ No ТТптгямгам Sk,(t) n Покажем, что гипотеза допустима. St Рассмотрим уравнение (1), учитывая синхронный режим работы системы. Получим lim e, (t) = lim p E, (p); r^co p^0 ' limx, (?) = lim pXt (p), t—>CG p—>0 где Xi (p) – изображение по Лапласу функции Xi (t); Ei (p) – изображение по Лапласу функции ei (A p – переменная преобразования Лапласа. Выразим EI (p) через передаточную функцию фильтра Калмана WI (p) и изображение XI (p): \(mpEAp)^mp\XAp)-XAp p^>0 p^0 x = \(тр^ХАр)-(ЕАр)Х, (p)) = p^0 = limp XAp)(l - (EAp)) , ek^t) St -^--2ak1 (?)- 2k"(t) где 10 (p) для случая синхронного режима работы в соответствии с рис. 2 можно записать в виде Решение уравнения (3) имеет вид: 1 l I . J24(C + ?)) k,U) = —ocNn+ — v4th ------ 2 2 ( JV0 J Л= .[nIoNnN, Ik w,№-^ 2k, ан--- О J C учетом этого в установившемся режиме получим где C – постоянная величина, определяемая начальными условиями. Тогда G,=201g НтеД?) ?—>co_________ limx, (?) ?^-GO ' = 201g 2k, No Проведя аналогичные вычисления, можно получить идентичный результат для квадратурного канала: G,=201g lime0(t) limxg (/) -201g ^Q Очевидно, что GbGq<0 при любых положительных значениях a , kh kQ и No, что подтверждает, что динамический диапазон канального сигнала при применении дифференциального преобразования будет уменьшен относительно исходного сигнала. Покажем, что разностные сигналы синфазного и квадратурного каналов сохраняют ортогональность. Для этого должно выполняться условие В силу ортогональности снфазного и квадратурного сигналов м(хе(г)х/(0)=0. Таким образом, третье слагаемое равно нулю. Аналогичную операцию можно проделать для второго и четвертого слагаемых, тогда получим, что условие (4) выполняется, то есть разностные сигналы сохраняют ортогональность. Произведем оценку устойчивости решения. В соответствии со схемой, приведенной на рис. 1, необходимо оценить устойчивость экстраполято-ра, охваченного положительной обратной связью. Обозначим передаточную функцию охваченного положительной обратной связью звена в синфазном канале приема через W 1RX (p\ передаточную функцию экстраполятора через Wl ^. Тогда 07 (p\=wAp^ ^-wap> |м(е7(t) eQ (t))dt = 0. Поскольку в качестве экстраполятора используется фильтр Калмана- Бьюси, получим Преобразуем указанное условие: Jm^CO eQ ^■(p) = 2k! aN^p+d) В установившемся режиме для устойчивости необходимо, чтобы откуда aN0 к, ol 2. Проверим решение (2) на соответствие указанному критерию: Первое слагаемое обращается в ноль по определению, исходные сигналы синфазного и квадратурного каналов являются ортогональными. Рассмотрим третье слагаемое подробнее: -^ 2a- 4tz2-4^- 4 v «j aN0 +CO Jm(^(o xe(o) dt = xo(t) w(?,,t)67t dt, Умножим числитель и знаменатель левой части на N0. Получим 2aN0 - TWA^4A4 aN0 4 < 2 5 2aN0 - ^4a2No-4Nu< 2aN0. где wdx,^ – функция веса экстраполятора. Поскольку функция xiW инвариантна относительно τ, внесем ее под знак интеграла. Также внесем под знак интеграла операцию математического ожидания (в силу независимости операций) и учтем, что функция веса инвариантна относительно переменной t. Получим j |м(хо(г)и,(/1,г)х7(Г)б/г) dt = -«0 = j Jw(/1,r)M(xc,(r)x7(Z)tZr) dt. Очевидно, что указанное неравенство будет выполняться для любых положительных значений a, k[, No и ^/. Аналогичное условие можно получить и для квадратурного канала. Таким образом, (2) позволяет получить на приеме устойчивое решение. Пример Рассмотрим в качестве примера систему широкополосной связи стандарта HSPA+ со следующими параметрами: выходная мощность 10 Вт; ширина полосы 5 МГц; центральная частота 2,1 ГГц; ско- рость передачи данных 10 Мбит/с; коэффициент CL = 7; СПМ помехи –70 дБм/Гц. Будем считать, что выходная мощность равномерно разделена между синфазным и квадратурным каналами, то есть PI и PQ равны 5 Вт. Тогда = 40 Вт; Сжатие динамического диапазона синфазного канала, таким образом, составляет 1,87 дБ, следовательно, можно уменьшить общую выходную мощность сигнала на 4,87 дБ. Проанализируем полученное решение с точки зрения энергоэффективности. Оценивать ее будем с помощью отношения скорости передачи R к потребляемой мощности передатчика P, необходимой для обеспечения указанной скорости _ R( бит/с) передачи: EnEf =— ---- . P V Вт ) Для оценки потребляемой мощности рассмотрим усилители производства Analog Devices, подходящие по частотному диапазону: HMC636ST89 (У1) и HMC639ST89 (У2). Усилители близки по характеристикам, отличаются только выходной и потребляемой мощностью: у усилителя У1 выходная мощность 40 дБм, У2 имеет 38 дБм; потребляемые мощности, соответственно, 0,775 Вт и 0,550 Вт. При заданной скорости передачи получим EnEf = 1 °'2'" = 13,53 ■ 106 ^^; 0,775 Вт EnEf = ^- = 19,07 - IO6 ^^. 0,550 Вт Очевидно, что энергоэффективность усилителя У2 выше, чем У1. С точки зрения более традиционного подхода, дифференциальная обработка позволяет уменьшить потребляемую мощность передающего блока на 0,225 Вт, что составляет 29%. Общее энергопотребление передатчика, таким образом, может быть снижено на 20%. Результаты компьютерного моделирования [10] показывают, что среднее уменьшение динамического диапазона сигнала составляет 2,49 дБ. Заключение Предложен метод дифференциального преобразования «по входу» с экстраполяцией на основе фильтра Калмана-Бьюси. Показано, что данный метод снижает динамический диапазон канального сигнала при сохранении ортогональности его синфазной и квадратурной компонент и устойчивости схемы восстановления сигнала на приеме.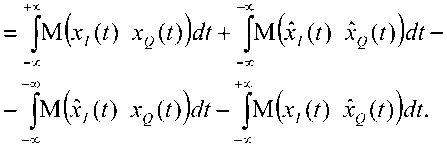
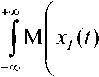
Список литературы Повышение энергоэффективности систем радиосвязи с ортогональным частотным мультиплексированием сигналов на основе их экстраполяции по Калману
- Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Пер. с англ. М.: ИД «Вильямс», 2003. - 1104 с.
- LTE for UMTS: OFDMA and SC-FDMA Based Radio Access / Еdited by Harri Holma and Antti Toskala - John Wiley & Sons, Ltd, 2009.
- ITU-R M.2047-0. Detailed specifications of the satellite radio interfaces of International Mobile Telecommunications-Advanced (IMT-Advanced).
- Markiewicz T.G. An Energy Efficient QAM Modulation with Multidimensional Signal Constellation // International Journal of Electronics and Telecommunications. V.62, №2, 2016. - P. 159-165.
- Кузнецов И.В., Султанов А.Х. Координированное управление динамическими объектами в сложных технических системах Уфа: Изд-во УГАТУ, 2012. - 207 с.
- Филатов П.Е. Повышение эффективности энергодефицитных многоканальных систем связи на основе координированного преобразования сигналов // Материалы МНТК «Прикладная электродинамика, фотоника и живые системы-2016» (ПРЭФЖС-2016). М.: 2016. - С. 143-148.
- Кузнецов И.В., Воронков Г.С., Султанов А.Х., Антонов В.В. Разработка дифференциального OFDM-преобразователя с координированным предсказанием сигналов для энергодефицитных систем связи // Радиотехника. №12, 2016. - С. 59-63.
- Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи: учебник для вузов. М.: Радио и связь, 1998. - 432 с.
- Изерман Р. Цифровые системы управления. Пер. с англ. М.: Мир, 1984. - 541 с.
- Воронков Г.С. Моделирование дифференциального преобразования сигналов OFDM для передачи изображений / Воронков Г.С. // Материалы МНТК «Прикладная электродинамика, фотоника и живые системы-2017» (ПРЭФЖС-2017). М.: 2017. - С. 17-20.


