Повышение качества управления в портах и терминалах

С развитием мировой транспортной системы всё более важную роль в управлении материальными и информационными потоками играют порты и наземные транспортные терминалы. Так, например, в «Транспортной стратегии Российской Федерации на период до 2030 гг.», определяющей транспортную политику государства, вопросам развития портов, контейнерных терминалов и наземных транспортных терминалов уделяется достаточно большое внимание.

В частности, делается акцент на обеспечении не только количественного, но и качественного роста – повышении производительности работы морских портов, использовании новых технологий, повышении уровня инновационности и качества услуг.

Решение данных задач невозможно без автоматизации управления всеми операциями с грузами, а, следовательно, невозможно без разработки и анализа системы управления, обеспечивающей необходимые показатели качества процесса управления.

Использование для перевозки грузов стандартных 20- и 40-футовых контейнеров позволяют автоматизировать значительную часть операций в контейнерном терминале.

Разработка модели процесса работы контейнерного терминала и создание на ее основе автоматизированной системы управления позволят повысить эффективность управления грузопотоками и таким образом обеспечить необходимый уровень качества предоставляемых услуг.

Контейнерные порты и терминалы имеют достаточно сложную структуру элементов и связей между ними, что ограничивает аналитические методы расчета параметров элементов и откликов на внешние воздействия [1, 2]. Данное ограничение способствует тому, что в настоящее время широкое распространение получили имитационные модели контейнерных портов и терминалов, которые позволяют исследовать поведение объекта во времени [3 – 6].

Однако, зачастую, такие модели не дают ответа на такие важные вопросы для процесса управления, как устойчивость, управляемость, наблюдаемость системы.

В общем случае морской контейнерный терминал в импортном направлении выполняет следующие операции: прибывшие морем контейнеры разгружаются с борта судна через морской грузовой фронт и перемещаются на площадку складирования груженых контейнеров импортного направления, с нее определенная доля контейнеров подается на досмотровый комплекс и после завершения операций досмотра возвращается на площадку, с площадки часть контейнеров покидает терминал без растарки, через автомобильный или железнодорожный грузовые фронты.

Таким образом, систему управления по обработке контейнеров импортного направления можно представить как систему с одним входом и одним выходом. Где входным воздействием является скорость поступления в систему (терминал) контейнеров, а выходным – уровень запасов, или количество накопленных в терминале контейнеров. Также в данной системе можно выделить две подсистемы: подсистему управления, отвечающую за обработку и перемещение контейнеров, и подсистему управления запасами.

Исследования систем управления такой конфигурации широко представлены в литературе по планированию и управлению цепями поставок и управлению производственно-сбытовыми системами [7 – 9].

Структурная схема системы управления контейнерным терминалом с передаточными функциями в форме изображения Лапласа, преобразованная из стандартной структурной схемы производственно-сбытовой системы представлена на рисунке 1.

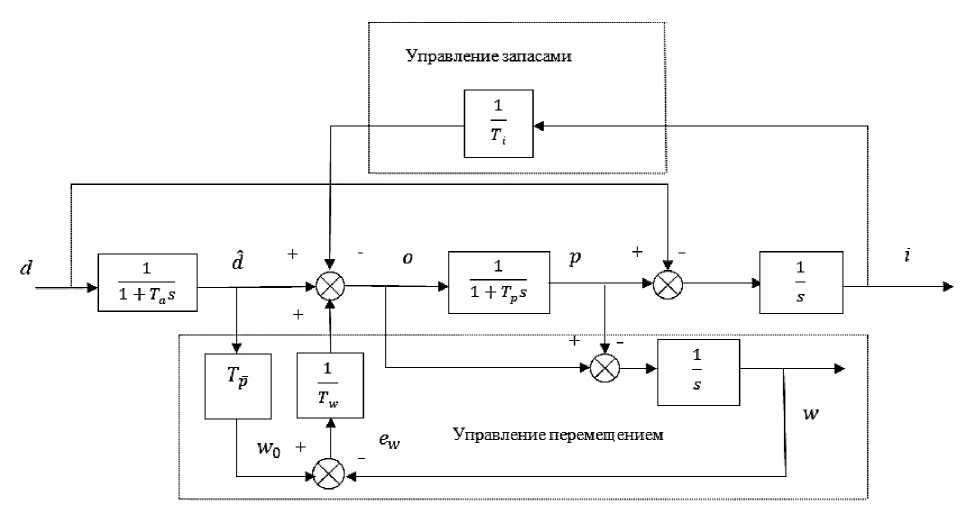
Рисунок 1 – Структурная схема системы управления контейнерным терминалом

В данной структурной схеме используются следующие обозначения:

• d(t~) - скорость прибытия контейнеров через морской грузовой фронт;

• p(t) - скорость поступления контейнеров на автомобильный или железнодорожный грузовые фронты для отправки наземными ви-

• дами транспорта;

• i(t) - фактическое количество ожидающих отправки контейнеров;

• d (t) - прогнозируемая скорость прибытия контейнеров;

• w(t) - фактическое количество контейнеров, находящихся в системе (в процессе обра-

• ботки);

• w_q (t) - требуемое количество контейнеров, находящихся в системе;

• e_w (t) - ошибка рассогласования между требуемым и фактическим количеством контейнеров, находящихся в системе;

  Ф($) = -Т

  
  

  (T p T w T t S²

  
  

o(t) - требуемая скорость обработки контейнеров, зависящая от фактического количества ожидающих отправки контейнеров, фактического количества контейнеров, находящихся в системе и прогнозируемой скорости прибытия контейнеров;

T, Tw - параметры управления, выража- ющиеся в единицах времени, позволяющие корректировать количество ожидающих отправки и находящихся в системе контейнеров;

T_a - постоянная времени экспоненциального сглаживания (средний период времени прогноза);

Tp - среднее время цикла обработки кон- тейнеров;

T p - ожидаемое время цикла обработки контейнеров, служит для компенсации задержек обработки контейнеров и равно T_p [10].

Передаточная функция замкнутой системы будет иметь следующий вид:

T p T_aT w S² + (T_aT p + T p T w + T_aT w )s + T p - T p

+ (Т_РТ + T w T> + T_w)(T a S + 1) ^.

Так как временные параметры T_p, T_w , T, T_a являются положительными величинами и, следовательно, коэффициенты характеристического уравнения тоже будут иметь положительные значения, то система будет асимптотически устойчива.

Запишем уравнения состояния системы в стандартной векторно-матричной форме:

x = Ax + Bd, (2) где собственная параметрическая матрица системы, вектор состояния, входная матрица и входной вектор имеют вид:

D(X) = |А-ЛЕ|

-1

T p T_t

-1

T t

-1

- 1

-1

T p T_w

-1

^T w

0    0

- 1

B = 0

-1

L T_a

0 T^p+Tw T p T_w T p +T_w .

-1

d = [d].

" Xi" Xp Xw . Xa.

Характеристическое уравнение системы,

представленной в пространстве состояний, бу-

дет иметь следующий вид:

X^T p T w T i X² + (T p T i + T w T i )A + T w )(T_aA + 1)

TpTaTwTi

где Е - единичная матрица.

Из выражения (3) видно, что один ко-

рень характеристического уравнения равен нулю, из чего следует, что система будет устойчивой, но не асимптотически.

Данного нулевого корня нет в характеристическом уравнении передаточной функции, что означает вырожденность передаточной функции системы, что, в свою очередь, приводит к потере управляемости системы. Это,

также, подтверждается следующим выражением

[11]:

- 1

L T B = [0 - T p 1 0]

0 =0,

- 1

L 1 a 3

где L Q - левый собственный вектор параметрической матрицы А, соответствующий нулевому собственному числу матрицы,

B - входная матрица.

Из равенства нулю выражения (4) следует, что данная мода неуправляема.

Для определения неуправляемых переменных состояния, соответствующих данной моде, нужно произвести преобразование подобия, приводящее матрицу А к диагональной форме:

г: = Az + LBd, (5) где A = LAR = diag(A_Q, Л 1 , Л₂, Л 3 ) - диагональная матрица, состоящая из собственных чисел матрицы А,

L = [Lo, Li, L2, Lgf, R = [Ro, Ri, R2, Rg] — матрицы, состоящие из левых и правых собствен- ных векторов соответственно,

LB = [0,31, 32,33]T - новая входная матрица с неуправляемой переменной zo, 31,32,33 — ненулевые компоненты матрицы, зависящие от параметров модели, z - вектор новых переменных, который связан с

вектором х следующим соотношением: 0     - Tp     1       0 - „       0        0     0        1 z = I^ = ,        ,        ,       , х (6) 131        (32       (33      (34 - U1       ^42      ^43      ^44- где Itj - ненулевые компоненты матрицы, зави- сящие от параметров модели.

Из выражения (6) видно, что неуправля- емая переменная zo связана с вектором х следу- ющим соотношением:

^z o     ^T p ^X p + ^Xw ■

Выражение (7) показывает, что переменные состояния x_p и X_w будут неуправляемыми.

Решение однородного дифференциального уравнения X = Ах с различными собствен- ными числами можно представить в следующем виде:

x(t) = coeZotRo + c1eA1tR1 + c2eZ2tR2 + сЛ,     (8)

где C_o, C 1 , с₂, с₃ - постоянные, зависящие от начальных условий.

В установившемся режиме при t ^ от и Ao = 0 решение (8) примет следующий вид:

х ⁽ от) = C o R o . (9)

Определив постоянные C_o, C 1 , C₂, с₃ из начальных условий х , (0), X_p(0), x_w(0), х ^ (0), выражение (9) примет следующий вид:

г -T , (X w (0) - T p X p (0))l

х(от) =

Т

w

X w ⁽ 0) - T_pX p (0)

или , .  -T(X w (0) -T p X p (0))

X j (от) =-----------T------------, (11)

X w ⁽ от) = X w ⁽ 0) - T p X p ⁽ 0).      (12)

Таким образом, при ненулевых начальных условиях x_w (0) ^ 0 и x_p (0) ^ 0 переменные состояния х , и x_w будут отличаться от требуемых значений.

На рисунке 2 показана реакция системы при начальных условиях xw(0) = 0,5 и Xp(0) = 0, T = Ta = Tp = Tp = 1, Tw = 0,5. Из рисунка

2 видно, что выходной параметр системы х, в установившемся режиме принимает значение отличное от нуля.

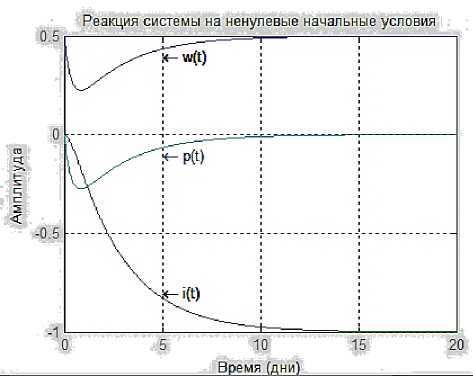
Рисунок 2 - Реакция системы при x_w(0) = 0,5.

Также, согласно теореме о конечном значении и выражению (1) для передаточной функции замкнутой системы, при постоянной величине внешнего воздействия, установившееся значение выходного сигнала примет вид:

d(s)

• х , (от) = lim----Ф(х)х =

s^o s

T-t

= -T,^—^d(s).    (13)

^T w

Таким образом, установившееся значе- ние выходного сигнала с учётом ненулевых начальных условий будет иметь вид:

X , (от) =

_ _ (T p- T p )d(t) - X w (0) + T p X p (0)

=T          ^

^T w

Качество системы управления контей-

нерным терминалом будет определяться с одной стороны обеспечением высокого уровня обслуживания потребителей, т.е. исключением ситуа- ции дефицита контейнеров на выходе (x, - отрицательное значение). С другой стороны, увеличение выходного объёма контейнеров (х, - положительное значение) будет негативно влиять на качественные и стоимостные показатели терминала. Таким образом, необходимо минимизировать отклонения выходного значения как в одну, так и в другую сторону, т.е. процесс должен быть максимально нечувствительным к отклонениям параметров от заданных значений.

Из выражения (14) видно, что параметры, влияющие на выходную величину можно разделить на две группы: управляемые параметры - T,, Tw, Tp, Tp и неуправляемые -d(t), Xw (0), Xp (0). Необходимо определить к отклонениям какого из управляемых параметров будет наиболее чувствительна выходная переменная с учётом влияния неуправляемых параметров.

Решению такого рода проблем были посвящены работы Г. Тагути в области управления качеством и робастного проектирования [12].

Идея метода Тагути состоит в том, чтобы вместо проверки всех возможных комбинаций значений полного набора параметров использовать сбалансированные ортогональные матрицы, в которых управляемые и неуправляемые параметры разделены на уровни. Выбор ортогональной матрицы зависит от количества используемых параметров и числа уровней.

Пусть управляемые параметры для контейнерного терминала будут иметь следующие значения [13]: T_t = 5, T_w = 0,5, T p = 1,5, T_p = 1 дней. Пусть входное воздействие d(t) = 1, тогда x_v = x_p = 1. Примем возможные отклонения параметров модели ±20% от исходных значений.

Следовательно, при расчётах будут использоваться четыре управляемых фактора, три неуправляемых фактора и три уровня.

В таблице 1 представлены значения управляемых и неуправляемых факторов на трёх уровнях.

Таблица 1 – Значения управляемых и неуправляемых факторов на трёх уровнях

Факторы	Значения уровней управляемых факторов
	Уровень 1	Уровень 2	Уровень 3
1. T	5	6	4
2. T v	0,5	0,6	0,4
3. T p	1,5	1,8	1,2
4. T p	1	1,2	0,8
Факторы	Значения уровней неуправляемых факторов
1. d	1	1,2	0,8
2. xw (0)	1	1,2	0,8
3. xp(0)	1	1,2	0,8

Для данных наборов факторов и уровней необходимо использовать ортогональные массивы L 9.

В таблице 2 представлен ортогональный массив L 9 для четырёх факторов и трёх уровней.

Ортогональный массив L 9 для трёх факторов и трёх уровней аналогичен массиву L 9 для четырёх факторов и трёх уровней и содержит три столбца.

В качестве характеристики качества используется критерий, измеряемый в децибелах, называемый «отношение сигнал/шум».

Так как выходной характеристикой является количество ожидающих отправки контейнеров, то функция потерь будет увеличиваться с увеличением отклонения выходной характеристики от заданного значения и, в случае, когда заданное значение равно нулю, функция потерь будет пропорциональна величине выходной характеристики.

Таблица 2 – Ортогональный массив L 9

№ реализа-ции	Уровни управляемых факторов
	T	T 1 v	1 p	T 1 p
1	1	1	1	1
2	1	2	2	2
3	1	3	3	3
4	2	1	2	3
5	2	2	3	1
6	2	3	1	2
7	3	1	3	2
8	3	2	1	3
9	3	3	2	1

Таким образом, в случае, когда цель – как можно меньшее значение выходной характе- ристики, выходная статистика определяется по формуле:

SN = —10log₁₀

(=S4

где SN - отношение сигнал/шум, вычисляе- мое для каждой реализации управляемых пара- метров,

у_;- - выходная характеристика, в данном случае - Х [ , вычисляемая для одной реализации управляемых и п реализаций неуправляемых параметров ( п = 9).

Результаты вычислений представлены в таблице 3.

Таблица 3 – Значения отношения сигнал/шум

№ реали- зации	Уровни управляемых факторов
	T	T 1 v	T 1 p	1 p	SN
1	1	1	1	1	-14.9136
2	1	2	2	2	-16.9574
3	1	3	3	3	-11.3830
4	2	1	2	3	-20.0987
5	2	2	3	1	-9.7497
6	2	3	1	2	-18.5388
7	3	1	3	2	-8.2764
8	3	2	1	3	-11.3467
9	3	3	2	1	-18.5150

Оценки среднего отношения SN для всех уровней факторов определялись как среднее значение для каждого уровня факторов. Результаты вычислений приведены в таблице 4.

Таблица 4 - Оценки среднего отношения SN

Факторы	Оценки среднего отношения SN для трёх уровней факторов
	Уровень 1	Уровень 2	Уровень 3
1. Г	-14.4180	-16.1291	-12.7127
2. Tw	-14.4296	-12.6846	-16.1456
3. Т р	-14.9331	-18.5237	-9.8031
4. Г	-14.3928	-14.5909	-14.2761

Средние значения отношений SN для каждого уровня четырёх факторов представлены на рисунке 3, где пунктирная линия – общее среднее значение, цифры на горизонтальной оси соответствуют номеру фактора из таблицы 4, точкой на графике обозначено среднее значение SN для каждого уровня фактора.

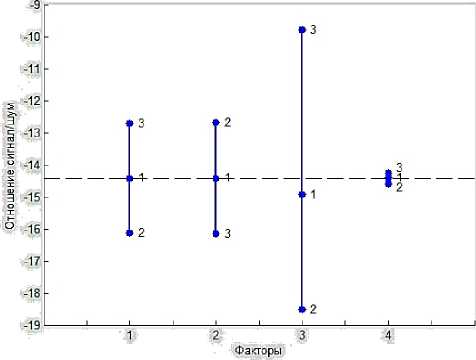
Рисунок 3 - Средние значения отношений SN для каждого уровня четырёх факторов

Проведённые расчёты показывают, что наибольшее воздействие на отношение сиг-нал/шум оказывает фактор Г р и наименее чувствительна выходная характеристика к фактору Т_р. Т.е. выходная характеристика в гораздо большей степени подвержена влиянию планируемого времени обработки контейнера в терминале, чем влиянию реального времени обработки.

Одним из возможных путей повышения качества системы управления, в данном случае, является своевременная проактивная или реактивная коррекция оценки времени обработки контейнера в ответ на возможные или произошедшие колебания времени цикла.