Повышение объективности оценки колебаний качества горной продукции

Горная продукция (руда, уголь и т.п.), добываемая на карьерах и рудниках, шахтах и разрезах, служит сырьем для потребителей – обогатительных фабрик и комбинатов, металлургических заводов и тепловых электростанций. Качество горной продукции – многофакторная величина, так как о нем судят по совокупности показателей качества. Показателями качества руды являются: дробимость, влажность, содержание полезных и вредных компонентов, крупность вкрапленности и многие другие. Качество угля характеризуется такими показателями, как влажность, размолотоспособность, зольность, калорийность (теплотворная способность), выход летучих, химический состав золы и т.д. В каждом конкретном случае состав и число показателей качества могут быть различными. В этой роли выступают такие характеристики сырья, которые влияют на эффективность тех или иных технологических операций.

Показатели качества, как правило, оказывают либо позитивное, либо негативное влияние на технологический процесс и конечный результат. Увеличение показателей, имеющих позитивное влияние, и уменьшение негативных показателей приводят к повышению качества горной продукции. Наоборот, уменьшение позитивных и увеличение негативных показателей снижает качество сырья. Однако отношение конкретного потребителя к качеству сырья определяется не только этим.

Потребитель настраивает технологию производства в зависимости от качества поставляемого ему сырья, стремясь добиться наибольшей эффективности его использования. При некотором изменении качества сырья в любую сторону и сохранении прежних значений параметров оборудования и технологических процессов потребление сырья происходит не в оптимальном режиме, КПД оборудования падает. Значительное изменение качества сырья вообще делает невозможным его использование данным потребителем. Поддержание соответствия между каче-

Добывающее предприятие должно выполнить трудную задачу - не только сохранить заложенное природой качество горной продукции, но и обеспечить постоянство этого качества. Причем постоянство качества должно быть обеспечено как в определенных объемах добычи (суточной, сменной), так и в отгружаемых потребителю партиях. Средние значения показателей качества по месторождению, как правило, известны благодаря геологоразведочным данным. Именно это качество сырья стремится обеспечить добывающее предприятие и на эти значения показателей качества настроена технология потребителя. Однако в объеме месторождения качество сырья может заметно меняться. Это является причиной колебаний качества в потоке добытого сырья, избежать этих колебаний невозможно.

Чего же может добиться добывающее предприятие? Оно применяет определенную технологию добычи и может управлять параметрами этой технологии. От применяемой технологии зависит, какими будут средние значения показателей качества сырья, а также амплитуда и период их колебаний относительно средних значений. Постоянство качества добываемого и поставляемого потребителям сырья обеспечивается планированием и ведением горных работ в режиме усреднения: местом и временем введения в строй забоев, регулированием нагрузки на забой, а также соединением потоков сырья от забоев в единый поток добывающего предприятия, применением подшихтовочных складов и многим другим. Как правило, этим добывающее предприятие решает задачу поддержания на постоянном, заявленном уровне средних значений показателей качества в поставляемых потребителям партиях сырья.

Потребитель тоже проверяет среднее значение качества по всей поставленной партии сырья. Если при этом колебания качества в пределах партии им не проверяются, то это не может интересовать и добывающее предприятие. Однако чем больше амплитуда таких колебаний, тем больший ущерб несет потребитель. И в его интересах следить за такими колебаниями.

Колебания качества сырья исследуют с помощью функции качества. В этой роли выступает один из наиболее важных для технологического процесса показателей качества сырья. Необходимо, чтобы это был количественный показатель, т. е. характеризующий качество числом. Значение показателя качества (число) определяется экспериментально в соответствии со стандартной методикой. Независимо от вида сырья, выбранного показателя качества и методики определения его значения для проведения эксперимента необходимо некоторое количество сырья – проба. Поэтому сам процесс такого экспериментального определения качества часто называют опробованием.

Масса пробы определяется требованиями методики и далее обозначается m0. Число к, полученное в результате опробования, представляет собой среднее значение показателя качества по массе пробы и характеризует только материал пробы. Проба очень мала по сравнению с объемами сырья, проходящими через оборудование предприятия за смену. Чтобы следить за качеством всего сырья, отбирают представительные пробы. Такая проба отбирается от партии сырья массой m1 по специальной методике, разработанной в соответствии с государственными стандартами. Методики отбора не налагают жестких ограничений на массу m 1, поэтому часто ограничиваются взятием одной представительной пробы от всей вновь доставленной партии сырья.

Отобранный при взятии представительной пробы материал подвергают обработке и в итоге получают несколько равноценных проб массой m ⁰. По одной из них определяют значение показателя качества, остальные хранят некоторое время для контроля. Таким образом, в результате опробования сырья по представительной пробе получают число k , которое является средним значением данного показателя качества по партии сырья массой m 1 . Ниже для краткости масса m ¹ называется массой представительной пробы.

Результаты опробования к 1 ,k ₂,..., k n поступающих последовательно партий сырья массой m 1 ¹, m 2 ,..., m n рассматривают как значения функции качества K , которые задают функцию таблично. В случае необходимости обработка этих данных (например интерполирование) позволяет получить аналитическое задание функции. Для визуализации данных по табличной или аналитической записи функции строят ее график.

В таблице 1 представлены данные зольности бородинского угля, поставляемого на ТЭС Ачинского глиноземного комбината с 1 по 15 ноября 2006 г. Зольность угля - один из важнейших показателей его качества – может служить функцией качества угля. Содержащаяся в таблице информация позволяет рассматривать зольность как функцию времени или массы. Время – более привычный и понятный аргумент функции. Неслучайно в теории усреднения используется функция качества, зависящая от времени. Однако при этом отмечается, что при исследовании колебаний качества необходимо знать размеры партии сырья, в пределах которой рассматриваются эти колебания. От массы партии сырья зависит влияние колебаний его качества на технологический процесс. Колебания качества в пределах малых партий сырья вообще не влияют на технологический процесс, какими бы сильными ни были эти колебания. Следовательно, изучению подлежат колебания качества сырья в зависимости от его массы. Для этих целей более удобной, хоть и менее привычной, будет функция качества, аргументом которой является масса. Именно такая функция K ( m ) используется в данной работе. Она позволяет строить более простые и информативные математические модели усреднения [1, 2].

На рисунке 1 построен график зольности угля в зависимости от его массы по данным табл. 1. По горизонтальной оси отложены нарастающим итогом массы партий угля в порядке их поступления на ТЭС, по вертикальной - значения к, функции качества K(m) - зольности угля, найденные по представительным пробам от этих партий. График имеет ступенчатый вид, ступеньки разной ширины, так как массы партий неодинаковы. Среднее значение функции качества вычисляют по формуле n k = M Tm mk,                                                  (1)

i =1

где M = ml + m2 +... + mn - суммарная масса всех партий, n - число партий. Заметим, что формула (1) позволяет найти среднее по массе M значение функции качества сырья. При добавлении новых данных изменится как масса M , так и найденное по ней среднее значение. Если массы партий можно считать одинаковыми, то пользуются более простой формулой к = -1(к + к, +... + к ). n х 1        2               n /

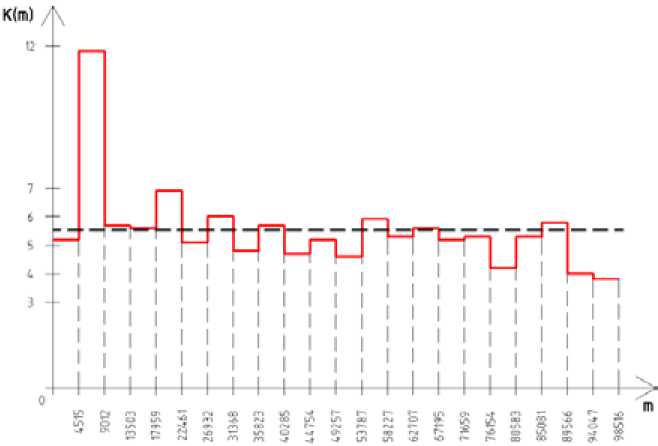
Рис. 1. График функции зольности бородинского угля

Таблица 1. Зольность бородинского угля

Время отбора пробы	Масса партии угля m 1 , т	Зольность угля A d , %	Время отбора пробы	Масса партии угля m 1 , т	Зольность угля A d , %
01.11.06 01:00	4515	5,2	08.11.06 12:40	4530	4,6
01.11.06 16:10	4497	11,8	08.11.06 23:40	4490	5,9
03.11.06 13:00	4491	5,7	09.11.06 10:20	4430	5,3
03.11.06 23:40	4456	5,6	10.11.06 05:10	4488	5,6
04.11.06 16:01	4502	6,9	11.11.06 05:00	4464	5,2
05.11.06 05:40	4471	5,1	11.11.06 23:45	4495	5,3
06.11.06 10:00	4436	6,0	12.11.06 11:45	4429	4,2
06.11.06 14:45	4455	4,8	13.11.06 13:00	4498	5,3
06.11.06 23:30	4462	5,7	14.11.06 06:00	4485	5,8
07.11.06 04:40	4469	4,7	14.11.06 14:57	4481	4,0
07.11.06 14:30	4503	5,2	15.11.06 14:58	4469	3,8

Применение формул (1) и (2) к данным табл. 1 дает практически не отличающиеся значения 5,534 и 5,532. На рисунке 1 среднее значение отмечено пунктирной линией.

Важной характеристикой колебаний функции качества является средняя амплитуда колебаний. Существует несколько формул разной степени точности для расчета этой величины. Наиболее часто применяется формула среднего квадратического отклонения:

n ₁

ст = ст ( K ) = (^ £ ( k i - к )²)².

i =1

Таблица 2. Пример двух функций качества одного и того же сырья

№ партии	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Масса партии	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1
ki 1	7	15	10	8	14	6	9	13	12	8	11	15	13	7	10	6
№ партии	1		2		3		4		5		6		7		8
— Масса партии	— 2 m		— 2 m 1		2 m 1		2 m 1		2 m		2 m 1		2 m 1		2 m 1
k i 2	11		9		10		11		10		13		10		8

Квадрат этой величины называется дисперсией и представляет собой среднюю энергию колебаний функции качества.

Рассмотрим на примерах простые, но важные свойства функции качества. Данные первого примера приведены в табл. 2. По значениям k ₁¹, k ₂¹ ,..., k ₁¹₆ функции качества K ¹( m ) и формулам (2) и (3) найдены k ¹ = 10,25 и σ¹ = 3,13.

Если за качеством того же сырья следить по представительным пробам от партий массой 2 m ¹, получим функцию качества K ²( m ), значения которой:

2 1 1 1    2 1 1 1    2 1 1  1

k 1 2 ( k 1 + k 2 ),        k 2 2 ( k 3 + k 4 ),---,      k 8 2 ( k 15 + k 16 )

также приведены в табл. 2. Среднее значение k ² = 10,25 такое же, как у функции K ¹( m ), а среднее квадратическое отклонение σ¹ = 1,49 меньше, чем σ¹. Графики обеих функций построены на рис. 2.

Таким образом, найденные по результатам опробования функция качества и оценка σ средней амплитуды ее колебаний зависят не только от истинного качества сырья, но и от массы представительных проб. Экспериментальные данные не содержат информации о колебаниях качества внутри партий сырья, от которых брали представительные пробы. Чем крупнее эти партии, тем больше энергии колебаний остается неучтенной в функции качества и тем меньше оценка σ. Учитывая это, найденную экспериментально функцию качества будем обозначать K ( m ¹, m ). Тогда K ¹( m ) = K ( m ¹, m ) и K ²( m ) = K (2 m ¹, m ). Возникает вопрос, какой должна быть масса m ¹, чтобы функция K ( m ¹, m ) обладала достаточной для практических целей точностью.

Рассмотрим следующий пример. В таблице 3 содержатся данные о четырех функциях качества, а на рис. 3 приводятся их графики. Функции описывают качество четырех вариантов сырья. Между функциями много общего: массы представительных проб, средние значения k = 6 и средняя амплитуда колебаний ст = 8/V15 ® 2.07.

Они отличаются только периодом колебаний: у функции K ³( m ¹, m ) он равен 16 m ¹, у K ⁴( m ¹, m ) – 8 m ¹, у K ⁵( m ¹, m ) и K ⁶( m ¹, m ) – 4 m ¹ и 2 m ¹ соответственно.

Какой из этих вариантов сырья больше соответствует оборудованию и технологии потребителя? Это зависит от оборудования. Любое оборудование – дробилки, мельницы, бункеры, флотационные или топочные камеры – взаимодействует с тем количеством сырья, которое находится внутри него. Результат работы оборудования и его износ зависят не от колебаний, а от средних значений показателей качества по данному количеству сырья. Все оборудование предприятия связано технологическим процессом. Одни единицы оборудования, обрабатывая – 407 –

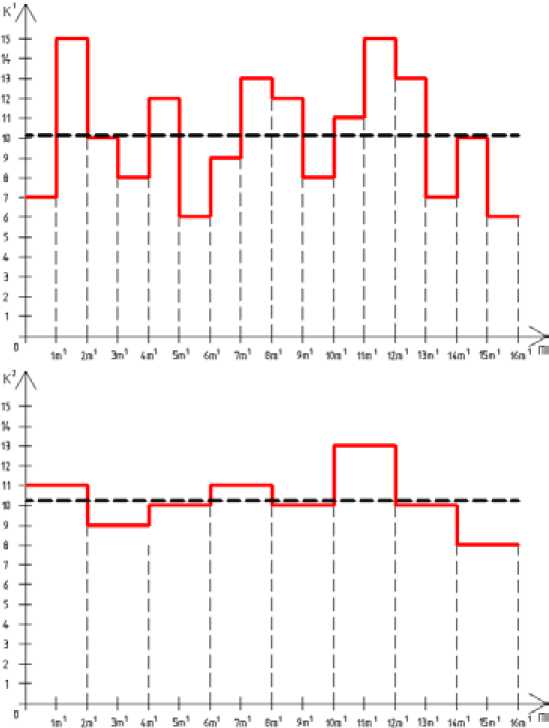
Рис. 2. Графики функций качества по данным табл. 2

Таблица 3. Пример функций качества четырех вариантов сырья

№ партии	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	k
Масса партии	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1	m 1
K 3( m 1, m )	8	8	8	8	8	8	8	8	4	4	4	4	4	4	4	4	6
K 4( m 1, m )	8	8	8	8	4	4	4	4	8	8	8	8	4	4	4	4	6
K 5( m 1, m )	8	8	4	4	8	8	4	4	8	8	4	4	8	8	4	4	6
K 6( m 1, m )	8	4	8	4	8	4	8	4	8	4	8	4	8	4	8	4	6

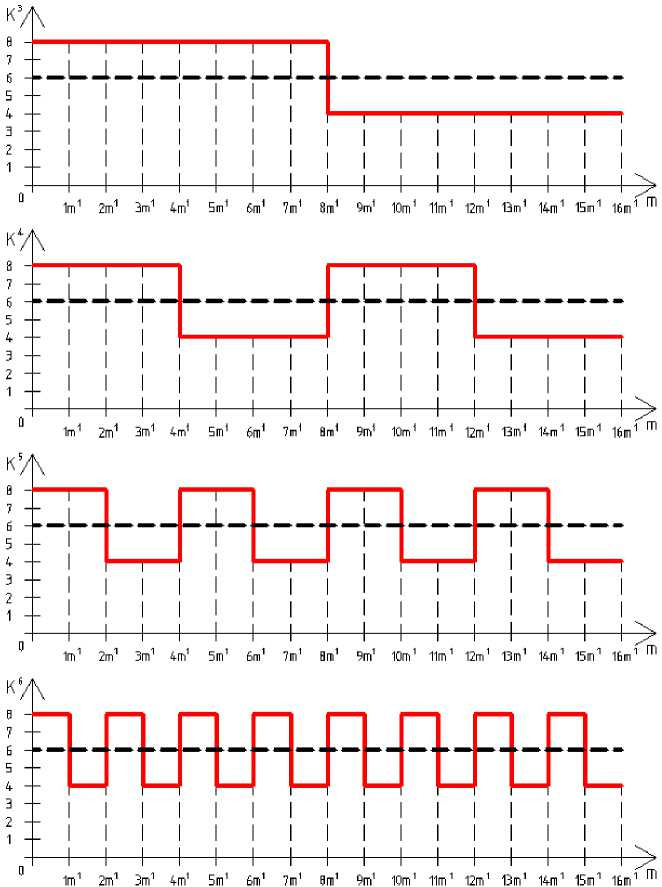
Рис. 3. Графики функций качества четырех вариантов сырья сырье, готовят его для следующих единиц. При этом почти любое оборудование, обрабатывая сырье, делает его более однородным. Поэтому наиболее крупное оборудование, стоящее обычно в начале технологической цепи, определяет то количество сырья, колебания качества внутри которого не влияют на технологический процесс предприятия в целом. В теории усреднения объем такого количества сырья называется единичным объемом. По аналогии массу единичного объема назовем единичной массой сырья и обозначим me.

Пусть в рассматриваемом примере сырье поставляется на предприятие, у которого m e = 4 m 1 . Тогда предприятие должно следить за теми колебаниями качества сырья, период которых превышает 4 m 1 , а колебания с меньшим периодом игнорировать. Как это удобнее сделать? При взятии представительной пробы массой m ¹ информация о колебаниях качества в пределах

– 409 –

Таблица 4. Оценка качества четырех видов сырья

№ партии сырья 1 2 3 4 k σ Масса партии сырья 4m1 4m1 4m1 4m1 K3(4m1, m) 8 8 4 4 6 4/V3 K4(4m1, m) 8 4 8 4 6 4/V3 K5(4m1, m) 6 6 6 6 6 0 K6(4m1, m) 6 6 6 6 6 0 массы m1 теряется, остается информация только о среднем значении. Чтобы учитывать энергию колебаний с периодом большим 4m1, предприятие должно брать представительные пробы массой 4m1 и анализировать функцию качества K(4m1, m). В таблице 4 приведены результаты такого применения, которые показывают, что третий и четвертый варианты сырья имеют стабильное качество (σ = 0), а первый и второй – нестабильное качество (σ = 4/ V3 ) для данного предприятия.

Теперь можно сформулировать ответ на поставленный ранее вопрос: анализ качества сырья следует проводить по представительным пробам от партий сырья, массы которых равны единичной массе сырья данного предприятия.

Единичная масса сырья многих ТЭС (включая и ТЭС Ачинского глиноземного комбината) не превышает нескольких десятков тонн. Взятие представительной пробы от всего прибывшего состава с углем массой около 4500 т не позволяет предприятию следить за опасными для него колебаниями качества угля, так как эта масса превышает единичную массу предприятия на два порядка.

Единичная масса сырья любого предприятия существенно меньше массы поступающих на него партий сырья. Разделение поступившей партии массой M на партии массой m_e , взятие от них представительных проб с последующим их анализом во много раз (возможно, на несколько порядков) увеличивают число опробований и затраты, с ними связанные. Однако возможен следующий подход. После такого разделения представительные пробы берут только у 4-8 партий массой m_e , равномерно распределенных по массе M . Например, партия сырья поступила в сорока вагонах, единичная масса сырья соответствует половине вагона. Выбираем вагоны с порядковыми номерами: 5, 10, 15, 20, 25, 30, 35 и 40 и берем представительные пробы сырья от половины каждого из этих вагонов. Полученная функция качества позволяет получить оценку σ, учитывающую колебания с периодами больше m_e .