Повышение помехоустойчивости систем связи на основе применения канальных сигналов с изменяющимися частотными характеристиками

Постановка проблемы

Возрастающая потребность пользователей в информационном обмене с высоким качеством обслуживания на различные расстояния независимо от места их нахождения привела к необходимости активного применения для этих целей спутниковых систем связи, в которых достаточно часто по ряду причин, изложенных в [1], в качестве переносчиков информации используются широкополосные сигналы (ШПС). Однако в техногенных условиях современных промышленных городов в полосе частот, выделенных спутниковым системам связи, присутствуют узкополосные помехи, возникающие в результате деятельности промышленных предприятий [2]. Сосредоточенные по спектру аддитивные помехи ухудшают помехоустойчивость систем, использующих ШПС.

Исходя из этого, для повышения достоверности приема информации в спутниковых системах связи возникает необходимость разработки ШПС, устойчивых к сосредоточенным по спектру помехам. В статье предлагается новый метод формирования ШПС, основанный на применении собственных векторов субполосных матриц с малыми значениями собственных чисел, в которых распределение частей их энергий в частотной области может быть изменено в зависимости от помеховой обстановки.

Математические основы формирования широкополосного сигнала

В предлагаемом методе используется принцип формирования ШПС, основанный на решении вариационной задачи по минимизации энергии сигнала в выбранном частотном интервале:

||x||“-Pr = Г(1-А,.)-х = max, (i)

где – энергия в заданном частотном интервале, ширина которого равна (^₊i -v_rY, I = diag (1,..., 1) – единичная матрица; ||,x|| – полная энергия сигнала; x – сигнальный вектор; x' – т анспонированный сигнальный вектор; ^Ar = К } – субполосная матрица, соответствующая r -му частотному интервалу с элементами вида:

s i п[уД /-/<)]- s i n[v,, (/ - ^

Здесь предполагается выполнение неравенства О < V,. < V_r+1<  71 . Для формирования канальных сигналов необходимо вычислить собственные векторы и собственные числа матрицы A,.. Для формирования ШПС целесообразно воспользоваться ортогональным базисом, состоящим из набора собственных векторов, приведенным в [3]:

Q = <4k^w..,q_N> Qj – собственные векторы субполосных матриц; X] – собственные числа векторов q j ; ^k ~ A+l ~ ••• ~ ^jV ~ 0 , где i = k,..,N.

Таким образом, формирование ШПС происходит следующим образом:

x = 0 e;                (3)

где X – ШПС; ^ ^— (^ei , ^ei VI ^ej ) – информационный вектор; ^J – передаваемый символ.

Необходимо отметить, что энергия сигнала за пределами заданного частотного интервала вычисляется согласно выражению вида:

ЕПР = Ъ^-^.      (4)

Z=1

Так как субполосные векторы ортогональны, то для восстановления информационного вектора необходимо воспользоваться следующим соотношением:

e-Qr x.          (5)

Согласно (4) предлагаемый метод позволяет сформировать ШПС x с минимальной энергией в заданном частотном интервале, что позволит избежать влияния сосредоточенной по спектру помехи при совпадении частотного диапазона помехи и интервала с минимумом энергии сформированного сигнала при использовании когерентного метода приема.

Оценка влияния узкополосной помехи на широкополосные сигналы

Формирование сигнала согласно выражению (3) позволяет изменять частотный интервал, в котором энергия сигнала минимальна, за счет применения собственных векторов для различных субполосных матриц, которые рассчитываются в соответствии с выражением (2). Данный факт позволяет адаптироваться к узкополосным помехам, сосредоточенным в различных частях используемого для передачи информации частотного диапазона.

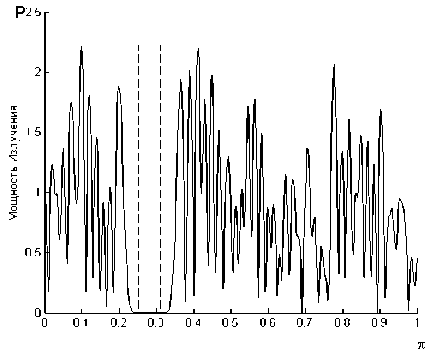
Рис. 1. Энергетический спектр субполосного вектора с близким к нулю собственным числом, минимум энергии в диапазоне от 0,25π до 0,32π

Как уже было отмечено выше, при Aj ) близких по значению к нулю, энергия собственного вектора практически полностью сосредоточена вне заданного частотного интервала (см. рис. 1), таким образом, локализация узкополосной поме- хи в частотном интервале, который не содержит энергетических составляющих передаваемого сигнала, не повлияет на достоверность когерентного приема сигнала, сформированного на основе собственных векторов субполосных матриц. Энергетические спектры сигналов, сформированные с применением собственных векторов для различных частотных диапазонов и ШПС, полученных на основе М-последовательности, представлены ниже.

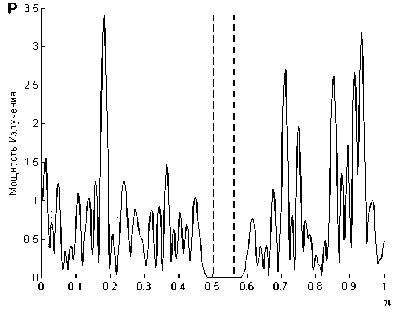
Рис. 2. Энергетический спектр субполосного вектора с близким к нулю собственным числом, минимум энергии в диапазоне от 0,5π до 0,57π

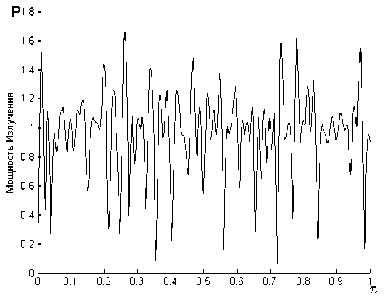
Рис. 3. Энергетический спектр широкополосного сигнала, полученного на основе применения М -пос-ледовательности

Для подтверждения эффективности разработанного метода была произведена оценка вероятности возникновения ошибки при приеме информационных последовательностей в условиях узкополосных помех, расчет которой осуществлялся по формуле [4-5]:

p = 1 A l^E‘^^ I (7)

где F(x) = .— je ^л *"dy , E – энергия сигнала; 7V₀ – односторонняя плотность шума;

J S (/ )5 0 + г ) exp (- j 2 л ft }dt x^,f^ = —--------—--------- j 5 Q )S (t )dt

– функция неопределенности, которая при j' = 0 фактически является автокорреляционной функцией [5].

Для определения вероятности ошибок были смоделированы широкополосные сигналы: с использованием собственных векторов с малыми значениями собственных чисел и ШПС, полученных на основе М -последовательности, а также узкополосные помехи различной энергии, которые складывались с сигналами. Для сигналов, суммированных с узкополосными помехами, рассчитывался коэффициент корреляции с сигналом, не подверженным влиянию помех (опорный сигнал приемного устройства, необходимый для когерентной корреляционной обработки). Полученные данные подставлялись в формулу (7). Результаты представлены в таблицах 1-2.

Таблица 1. Вероятность возникновения ошибки при приеме сигнала, сформированного на основе собственных векторов, подверженного воздействию узкополосной помехи

Отношение энергии сигнала к энергии помехи, дБ	Вероятность ошибки для сигнала, сформированного на основе собственных векторов, хЮ"6
	Частотный диапазон помехи совпадает с частотным интервалом	Частотный диапазон помехи не совпадает с частотным интервалом
20	6,95	10,5
18	6,94	10,6
16	6,93	10,8
14	6,92	11,0
12	6,91	11,3
10	6,90	11,7
8	6,88	12,2
6	6,86	12,8
4	6,83	13,6
2	6,79	14,8
0	6,74	16,4
-2	6,69	18,6
	6,61	21,9
-6	6,52	26,8
-8	6,41	34,6
-10	6,28	47,9
-12	6,11	71,9
-14	5,90	120,0
-16	5,66	231,0
-18	5,36	525,0
-20	5,01	1500,0

Согласно полученным результатам для ШПС, сформированных на основе М последовательностей, увеличение энергии узкополосной помехи приводит к увеличению вероятности ошибки при приеме сигнала. Режекция спектра сигнала в полосе частот узкополосной помехи уменьшает вероятность ошибки, однако вместе с помехой подавляется часть сигнала, что приводит к ухудшению помехоустойчивости. В свою очередь изменение вероятности ошибки при приеме широкополосного сигнала с применением собственных векторов субполосных матриц остается незначительным – вплоть до –20 Дб отношения энергии сигнала к энергии помехи составляет не более 2^.10^-6.

Таблица 2. Вероятность возникновения ошибки при приеме ШПС, полученного на основе М-последова-тельности, подверженного воздействию узкополосной помехи.

Отношение энергии сигнала к энергии помехи, дБ	Вероятность ошибки для ШПС, полученного на основеМ-последовательности, хЮ"6
	Без режекции спектра	С применением режекции спектра
20	9,17	44,8
18	9,30	44,8
16	9,48	44,9
14	9,70	44,9
12	9,99	45,0
10	10,4	45,1
8	10,9	45,3
6	11,5	45,4
4	12,4	45,6
2	13,6	45,9
0	15,3	46,3
-2	17,7	46,7
—4	21,4	47,2
-6	27,0	48,0
-8	36,3	4.8,9
-10	52,6	51,0
-12	84,2	51,5
-14	152,0	53,5
-16	323,0	56,1
-18	837,0	59,5
-20	2810,0	64,1

Выводы

Результаты моделирования и расчеты вероятности ошибок показывают, что более устойчивым к воздействию сосредоточенной по спектру помехи является сигнал с применением собственных векторов субполосных матриц с малыми значениями собственных чисел, кроме этого, распределение энергии в частотной области предлагаемого сигнала может быть изменено в зависи- мости от помеховой обстановки. Совокупность данных свойств сигнала позволяет с уверенностью сказать, что его применение позволит повысить качество передачи информации в системах связи с ШПС в условиях воздействия на них узкополосных помех.