Повышение производительности мехатронных комплексов лазерной обработки на основе зависимости контурной погрешности от параметров движения и исполнительных систем
Автор: Заруднев А.С., Илюхин Ю.В.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 3 т.9, 2007 года.
Бесплатный доступ
Предложен закон движения рабочего органа лазерных комплексов, обладающих упругими меха- ническими компонентами, который повышает производительность при обеспечении требуемой контурной точности движения. Параметры закона движения оптимизируются на основании вы- явленной зависимости контурной ошибки в узлах желаемой траектории от скорости движения, геометрических характеристик сегментов траектории и динамических свойств исполнительных приводов и механических компонентов.
Короткий адрес: https://sciup.org/148198006
IDR: 148198006 | УДК: 621.26+004.451.25
Текст научной статьи Повышение производительности мехатронных комплексов лазерной обработки на основе зависимости контурной погрешности от параметров движения и исполнительных систем
где
| sin а | при 0 < 1 а < 0,5 п ,
1 при п > | а | > 0,5 п ;(7) ξω .min – значение коэффициента относительного демпфирования механической части с наименьшей частотой собственных колебаний; f 2 ( ω O . МIN , ω O . MAX ) – функция, характеризующая влияние динамических свойств исполнительных систем
f ( а ) = *
f 2 ( ω O . МIN
ω O . MAX
) = 1,5
ω О . МIN
ω О . МАХ
+ ------
2 ω С . П
(8) причём частота среза определяется в соответствии с правилом настройки следящих при-
водов по формуле (4).
Найденные эмпирические зависимости обладают приемлемой точностью. Об этом свидетельствуют графики (рис. 2) сравнения результатов вычислительного эксперимента (графики 1 и 3) и расчётов по предложенным формулам (6) – (8) (графики 2 и 4). Они получены для двухкоординатой системы управления движением при контурной скорости, равной 100 мм/с; переменных значениях частоты собственных колебаний ω О 1 одной из механических подсистем и фиксированных частотах собственных колебаний второй механической подсистемы ω О 2 , равных 105 с-1 (графики 1 и 2) и 55 с-1 (графики 3 и 4). Коэффициент относительного демпфирования для обеих механических подсистем равен 0,3, а угол между сегментами равен 90О.
Наибольшая погрешность определения максимальной относительной контурной ошибки по предложенным формулам (6) - (8) не превышает 26%. Поэтому они рекомендуются для построения алгоритмов выбора желаемой контурной скорости в узле траектории.
Повышение производительности при обеспечении заданной точности
На основании полученной зависимости желаемой контурной скорости от параметров траектории и динамических свойств механических подсистем сформирован закон движения рабочего органа и разработан алгоритм оптимизации значений его параметров в со-
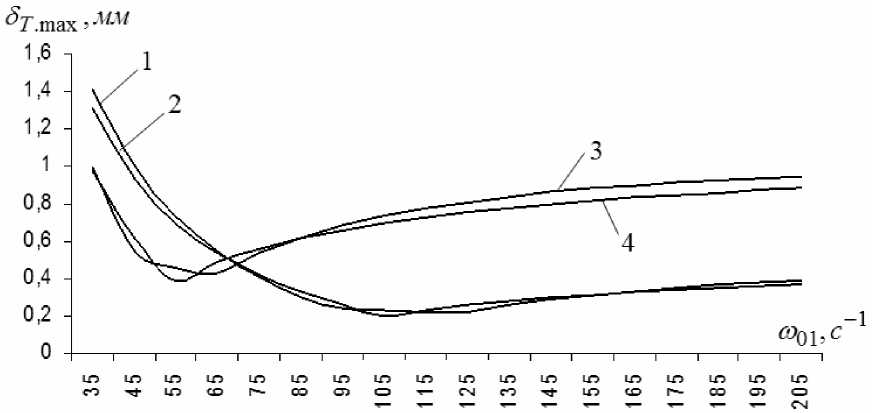
Рис. 2. Зависимость контурной ошибки от частот собственных колебаний механических частей
ответствии с требованием (1) и ограничениями (2) и (3). В соответствии с этим законом определяется желаемый путь L k ( t ) , который должен пройти рабочий орган вдоль k – го сегмента желаемой траектории в функции от времени t движения по этому сегменту
L k ( t ) =
akt 2
-
V HA4 t + 2
2 aktp
-
V HA4 t p + ^ + V HOM t
2 aktp
-
V HA Ч^р + ., + V HOM t n
akt 2 2
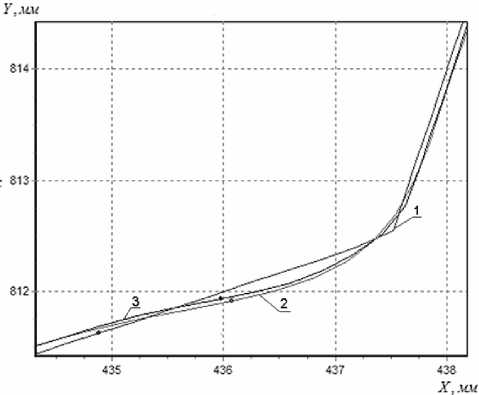
при 0 где VНАЧ и VНОМ – контурная скорость в начале сегмента траектории и номинальная контурная скорость, соответственно; аk – ускорение вдоль траектории; tP , tT , tП – времена разгона, торможения и движения с постоянной скоростью, соответственно, которые вычисляются в соответствии с уравнениями t VHOM VHA4 ak Lсег — (VHA4tp+ aktp tn = ) - (VHOMtT+ aktТ2 ) tT = VHOM VKOH ak VНОМ ; Здесь VКОН – контурная скорость в конце сегмента траектории. Путь Lk (t) является аргументом при определении желаемых координат рабочего органа, которые вычисляются с учётом типа и значений параметров каждого сегмента траектории. Значения параметров, характеризующих характер изменения контурной скорости выбираются максимально возможными и, таким образом, при использовании предложенного закона управления повышение производительности достигается в результате максимально быстрого движения рабочего органа через узлы траектории при соблюдении требований к точности и отсутствию разрывов контурной скорости в узлах. Разработан алгоритм определения оптимальных значений параметров предложенного закона управления движением рабочего органа, базирующийся на выявленных взаимосвязях точности исполнительных движений с геометрическими характеристиками траекторий, контурной скоростью движения и динамическими свойствами исполнительных систем. В результате анализа исходных данных о желаемой траектории этот алгоритм обеспечивает определение предельной контурной скорости на сегментах в виде отрезков прямых или дуг окружностей, а также в узлах траектории и максимальной допустимой скорости, реализуемой в узлах при разгоне и торможении. В результате работы алгоритма определяются все параметры закона управления, обеспечивающие минимальное общее время выполнения программы лазерной резки. Реализация системы и экспериментальное исследование точности и производительности Экспериментальная проверка результатов исследования выполнена с использованием разработанной авторами системы управления мехатронным лазерным комплексом, включающим в себя координатный стол с перемещениями 3400 х 2000 мм, цифровые исполнительные приводы на базе синхронных двигателей и преобразователей фирмы КЕВ и устройства управления на основе промышленного персонального компьютера с дополнительными периферийными устройствами. Комплекс имеет механические передачи в виде последовательно соединённых планетарных редукторов и зубчато-ремённых передач. Система оснащена специально разработанной программой управления, которая обеспечивает взаимодействие с пользователем, преобразует информацию о желаемой траектории и технологические данные в коды управления исполнительными приводами, лазером и вспомогательным оборудованием комплекса. При этом реализуется предложенный закон движения рабочего органа, минимизирующий затраты времени на обработку за счёт оптимизации профиля контурной скорости. Центральным в этой программе является блок оптимизации параметров закона движения. Программа написана на языке С++ в среде Borland C++ 3.11, работает под управлением операционной системы MS DOS 7.10 и обеспечивает жесткое реальное время с периодом квантования 3 мс. Рис. 3. Переходные процессы исполнительного привода Сравнение результатов математического моделирования и натурных экспериментов следящих приводов в составе лазерного комплекса показало качественное и количественное совпадение основных составляющих процессов, зафиксированных при моделировании и натурных экспериментах (рис. 3). На рис. 4 показаны: 1 – задающее воздействие, несущее информацию о желаемой скорости движения вала двигателя; 2 – процесс изменения скорости вала двигателя, полученный с помощью математической модели; 3 – процесс изменения скорости вала двигателя реального цифрового привода в составе лазерного комплекса, зафиксированный с помощью встроенного осциллографа. Среднеквадратичное отклонение скорости, полученной моделированием, от фактической скорости не превышает 10% Используемые в программе моделирования значения частот среза приводов получе- Рис. 4. Желаемая траектория движения рабочего органа (1), траектория, полученная путём моделирования (2) и фактическая траектория (3), зафиксированная в эксперименте. ны непосредственно по настроечным параметрам программно реализованных регуляторов положения и коэффициентам передачи фотоимпульсных датчиков положения. Значения частот собственных колебаний ωО1,…, ωОN и коэффициентов относительного демпфирования ξ1, …, ξN механических подсистем определены в результате идентификации параметров с использованием осциллограмм работы реальной системы. Исследование контурной погрешности также свидетельствуют о сходстве результатов, полученных экспериментально и путём моделирования (рис. 4). Экспериментальное исследование производительности системы, использующей предложенные закон движения и алгоритм оптимизации параметров, выполненное в компании “Лантан-Лазер”, свидетельствует о высокой эффективности предложенных алгоритмов управления. В частности, при выполнении управляющей программы лазерной резки с общей длиной реза более 32 м выигрыш производительности предлагаемой системы по сравнению с традиционной составил около 30%. При этом реальная результирующая контурная ошибка не превысила допустимый уровень, равный 100 мкм. Основные результаты исследования и рекомендации Полученные результаты исследования позволяют сделать вывод о том, что предложенные на основании математического моделирования и натурных экспериментов закон движения рабочего органа и алгоритм оптимизации его параметров обеспечивают повышение производительности лазерных комплексов, обладающих упругими механическими компонентами и предназначенных для резки деталей сложной формы. Предложенные закон движения и алгоритм могут быть также полезны для создания высокоэффективных систем управления ряда других технологических машин.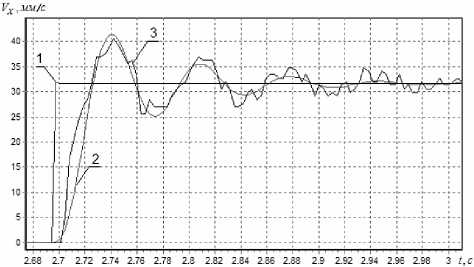
Список литературы Повышение производительности мехатронных комплексов лазерной обработки на основе зависимости контурной погрешности от параметров движения и исполнительных систем
- Подураев Ю.В. Мехатроника: основы, методы, применение. M: Машиностроение, 2007.
- Илюхин Ю.В. Синергетический (мехатронный) подход к проектированию систем управления технологических роботов//Мехатроника. 2000. № 2
- Илюхин Ю.В. Реализация мехатронного подхода при построении систем компьютерного управления комплексов лазерной и плазменной резки//Мехатроника, автоматизация, управление. 2005. №10
- Заруднев А.С., Илюхин Ю.В. Анализ точности движений лазерного комплекса//Сборник докладов IX-ой научной конференции по математическому моделированию и информатике. М.: МГТУ "Станкин" -ИММ РАН, 2006.


