Повышение пространственного разрешения сигналов в оптических системах

Непрерывный аналоговый сигнал можно представить дискретной последовательностью его значений (отсчетов). Эти отсчеты берутся в точках, отделенных друг от друга некоторым интервалом, который называется интервалом дискретизации. Пространственная частота – отношение периода сигнала к интервалу дискретизации. Интуитивно понятно, что чем меньше интервал дискретизации и, соответственно, чем выше частота дискретизации, тем меньше различия между исходным и восстановленным по дискретным значениям сигналами.

Теорема Котельникова [1 –4] определяет условия, при которых спектр одиночного сигнала можно вы- делить без искажений, и затем по ним восстановить исходный сигнал по набору дискретных величин. Однако интерполяция с помощью ряда Котельникова подразумевает бесконечное число отсчетов. При использовании конечного числа дискретных значений вычисления для непериодического сигнала приводят к некоторой погрешности [5]. Кроме того, идеальная дискретизация, которую можно представить как воздействие на функцию бесконечной гребёнки Дирака, является математической абстракцией.

Общая постановка задачи повышения пространственного разрешения в оптических системах описана в [6, 7]. На рис. 1 показана схема регистрации одномерного сигнала при его сканировании апертурой с низким разрешением. Здесь n – количество элементов низкоразрешающего растра, l – количество высокоразрешающих элементов, попадающих в интегрируемую апертуру Ii, I = 0…n, nl – количество элементов в высокоразрешающем растре.

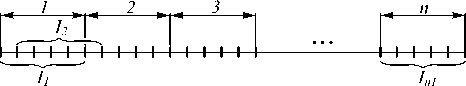
Рис. 1. Схема регистрации сигнала при субпиксельном сдвиге

Если в результате измерений мы получим набор значений с низким разрешением I i , сдвинутых относительно друг друга на некоторую величину, меньшую размера интегрированной апертуры, то можно определить высокоразрешающие элементы x i .

Прямой путь нахождения высокоразрешающих элементов – это решение системы линейных уравнений.

x 1 + x 2 +. . x i = 1 1

x 2 + x 3 + ... x + 1 = 1 2

^x ( n - 1) l + 1 ^{+ x} ( n - 1) l + 2 ⁺ • "  x nl I nl .

При увеличении числа сдвигов размер системы линейных уравнений получается очень большим. Основные исследования в этой области связаны с методами ускорения и повышения устойчивости решения системы (1) [6, 8–13].

Сверхразрешение достигается в процессе математической обработки, при которой создаётся изображение в более высоком разрешении из серии кадров изображения одного и того же объекта с более низким разрешением [14]. Фаза содержит больше информации об изображении, чем амплитуда [15].

В этой статье рассмотрен способ, основанный на анализе Фурье-образов изображений, полученных усреднением на площадках конечных размеров (апертурах).

Практически дискретизация осуществляется измерением сигнала с помощью датчиков с некоторой конечной апертурой (площадкой по которой происходит усреднение). Набор значений { f p ( r A x , k A y )} представляет дискретное преобразование сигнала.

Используются апертуры различных форм, например, эллиптические, ромбовидные, гексагональные, но наиболее часто используются апертуры прямоугольной формы (рис. 2).

Числовые значения отсчетов изображения получаются путем пространственного интегрирования по некоторой конечной площадке.

В [16] показано, что в этом случае спектр полученного изображения будет определяться следующим выражением:

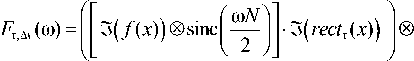
®combine (to), где [3 (f (x)) ® sinc (to^/2)] - дискретный Фурье-образ исходной функции, 3 (rectт (x)) - Фурье-образ используемой апертуры (апертурная функция), ® -обозначение операции свертки, comb(2n/Ax)(to) - гребенка Дирака, которая определяется как последовательность смещенных с шагом 2п / A x дельтафункций.

Это выражение (2) получено с использованием аппарата обобщенных функций [17–22].

Рис. 2. Примеры растров: слева – регулярный растр с прямоугольной апертурой; справа – с круговой апертурой

Целью этой статьи является рассмотрение вопросов восстановления высокоразрешающих элементов по спектру изображений, полученных усреднением на регулярных растрах с помощью выражения (2).

1.    Восстановление усредненных на регулярном прямоугольном растре изображений

На рис . 3 приведены исходное изображение размером 256×256 пикселей (слева) и изображение, каждая точка которого определяется усреднением по массиву 4×4 исходного изображения (справа). Таким образом, моделируется дискретизация с помощью регулярного растра прямоугольных апертур, сдвинутых на субпиксельную величину, равную 1 /4 шага дискретизации.

Рис. 3. Исходное и усредненное набором прямоугольных апертур 4 × 4 изображение 256 × 256 точек

Функция 3 ( rect т ( x )) = sinc ( toT /2) - амплитуда Фурье-преобразования окна на массиве 256 × 256 показана на рис. 4.

Из выражения (2) видно, что если Фурье-образ усредненного изображения параграфить на 3 (rect4 (to)), то получим Фурье-образ исходного изображения. Взяв от него обратное Фурье-преобразование, получим исходное. На рис. 5 показа- ны усредненное на регулярном прямоугольном растре и восстановленное изображения.

На рис. 6 приведены исходное изображение и изображение, каждая точка которого определяется усреднением на прямоугольном растре 8 × 8.

Вид апертурной функции и её Фурье-образ ℑ ( rect 8 ( x )) показан на рис. 7.

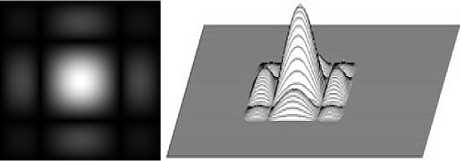
Рис. 4. Амплитуда Фурье-преобразования апертуры 4 × 4 с динамическим диапазоном от 0 до 1 и её 3D-график

Рис. 5. Усредненное на регулярном наборе прямоугольных растров (4 × 4) и восстановленное изображения

Рис. 6. Исходное и усредненное на регулярном наборе прямоугольных растров 8 × 8 изображения

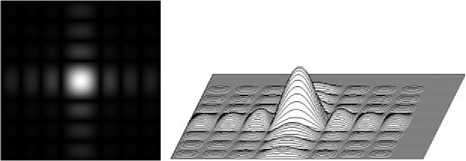
Рис. 7. Апертурная функция 8 × 8 точек (Фурье-образ прямоугольной апертуры). Справа: 3D-график функции (диапазон от 0 до 1)

На рис. 8 показаны усредненное на прямоугольных растрах 8 × 8 и восстановленное изображения.

Таким образом, по изображению, полученному усреднением на наборе апертур и сдвигом на определенную субпиксельную величину, можно восстановить исходное изображение, если известен вид апертуры.

В нашем случае рассмотрение велось для прямоугольной апертуры, но при замене, например, на

ℑ ( circ r ( x )) для апертуры в виде круга выражение будет верно для регулярных растров апертур в виде круга. Поскольку вид множителя ℑ ( circ r ( x )) известен, то можно найти спектр исходной функции.

Рис. 8. Усредненное на прямоугольном растре с апертурой 8 × 8 точек и восстановленное изображения

В следующем параграфе показан способ экспериментального получения апертурной функции для случая, когда её вид неизвестен. Этот способ возможен, например, при использовании двух микрообъективов с различным разрешением при вводе тестовых объектов.

2.    Экспериментальное определение апертурной функции

Для восстановления сигнала в спектральной области необходимо получить вид апертурной функции. Для прямоугольных апертур это ℑ ( rect τ ( x )), для круговых – ℑ ( circ r ( x )), но в реальных системах вид этой функции может быть произвольным.

На рис. 9 показаны два изображения с низким разрешением и высоким разрешением. Характеристика апертурной функции неизвестна.

Рис. 9. Изображения с низким (апертура 8 × 8) и высоким разрешением (апертура 2 × 2)

Из выражения (2) видно, что, параграфив Фурье-образ изображения с низким разрешением на Фурье-образ изображения, полученного с высоким разрешением, можно экспериментально определить вид апертурной функции. На рис. 10 показан вид апертурной функции, определенной экспериментально.

Вид этой апертурной функции можно использовать для восстановления произвольных изображений, полученных с одним разрешением.

На рис. 11 показано изображение, полученное из серии сдвинутых изображений с низким разрешением (апертура 8 × 8), и восстановленное с помощью апертурной функции, показанной на рис. 10.

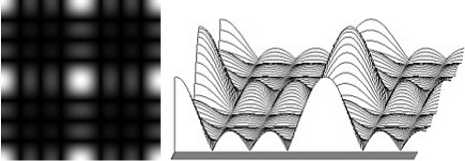
Рис. 10. Вид апертурной функции

Рис. 11. Результат восстановления изображения

Таким образом, если мы имеем устройство с низким разрешением, то возможно повышение разрешения с помощью апертурной функции, которая является характеристикой системы и может быть экспериментально получена с помощью тестовых объектов.

3.    Создание систем сверхразрешения на базе оптических микроскопов

Недостатком систем оптической микроскопии является фундаментальное ограничение на пространственную частоту. Это разрешение определяется критерием Рэлея (3):

R = 0,61

λ

NA obj ,

где NA^obj – числовая апертура, которая зависит от конструкции микрообъектива; λ – длина волны источника освещения. На практике при длине волны порядка 500 нм пространственное разрешение оптических микроскопов не превышает 200 нм.

Восстановление сигнала в промежутках между дискретными значениями имеет огромное значение при решении задачи пространственного сверхразрешения в оптической микроскопии. Для решения этой проблемы может использоваться сдвиг массива детекторов на часть элемента разрешения dx = Δ x / N , где Δ x – разрешение оптической системы.

Если у нас есть возможность перемещать изображение в объектной области микроскопа или матричный датчик на величину, меньшую разрешения оптической системы, то по серии изображений, оцифрованных с низким разрешением, можно восстановить изображения, соответствующие высокоразрешающим растрам при оцифровке (рис. 1).

Пусть у нас есть результаты оцифровки с низким разрешением нескольких изображений: A ( x , y ) – без сдвига, AXY ( x + dx , y + dy ) – со сдвигом по оси x и y, то мы можем сформировать изображение [12] по алгоритму, указанному в табл. 1. В табл. 1 показано сформированное изображение, увеличенное в 3 раза.

Из этого изображения можно выделить высокоразрешающие компоненты. Если есть возможность сдвига на большее число шагов, формируем новое изображение по такому же алгоритму. Точность восстановления будет зависеть от точности пространственного сдвига на субпиксельную величину.

Табл. 1. Формирование изображения при сдвиге матрицы фотодетекторов из изображений, зафиксированных с низким разрешением

A ( x 0, y 0)	AXY ( x 0+ dx , y 0)	AXY ( x 0+2 dx , y 0)	A ( x 1, y 0)
AXY ( x 0, y 0+ dy )	AXY ( x 0+ dx , y 0+ dy )	AXY ( x 0+2 dx , y 0+ dy )	AXY ( x 1, y 0+ dy )
AXY ( x 0, y 0+2 dy )	AXY ( x 0+ dx , y 0+2 dy )	AXY ( x 0+2 dx , y 0+2 dy )	AX ( x 1, y 0+2 dy )
A ( x 0, y 1)	AX ( x 0+ dx , y1)	AX ( x 0+2 dy , y 1)	A ( x 1, y 1)

Если разрешение системы необходимо увеличить в два раза, то необходимо сделать всего три шага при перемещении матрицы фотоприёмников на величину, равную половине разрешения (два раза на dx и один на dy ). Если необходимо увеличить разрешение в четыре раза, то необходимо 15 шагов (рис. 12).

Если необходимо увеличить разрешение в m раз, то общее число шагов будет m ( m – 1) при увеличении на dx плюс ( m – 1) при увеличении на dy . Всего ( m – 1)( m + 1) шагов при перемещении матрицы фотодетекторов.

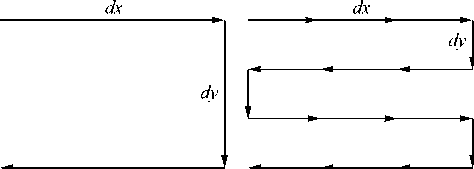
Рис. 12. Задание пространственных сдвигов с величиной сдвига, равной половине разрешения (слева: для увеличения разрешения в два раза, справа: для увеличения разрешения в 4 раза)

Возможны и другие виды обхода точек (кроме показанного на рис. 12) с другим числом шагов по направлениям dx и dy .

Общее число шагов может измениться, но схема обхода может зависеть от вида экспериментальной установки.

Заключение

В статье рассмотрена задача восстановления высоких частот изображений, усредненных на регулярном наборе растров. Эта задача достигается на основе рассмотрения аналитического выражения для спектра функции при реальной дискретизации (2). Выражение получено с использованием аппарата обобщенных функций. В отличие от идеальной дискретизации спектр функции дополняется множителем ℑ ( rect τ ( x )), вид которого несложно определить. Этот множитель зависит только от вида апертуры. В нашем случае рассмотрение велось для прямоугольной апертуры, но при замене, например, на ℑ ( circ r ( x )) для апертуры в виде круга выражение будет верно и для регулярных круговых растров.

Спектр апертуры обычно известная функция, поэтому если известен спектр изображения, полученного усреднением с некоторой апертурой, то можно получить и спектр исходного изображения. Применив операцию обратного Фурье-преобразования, можно восстановить исходное. Для случая, когда вид апертуры неизвестен, показан способ получения апертурной функции на основе сравнения спектров тестовых объектов.

При повышении пространственного разрешения с помощью устройств субпиксельного сдвига появляется возможность проводить исследования методами цифровой голографии объемных диффузных объектов с качеством аналоговой (при регистрации на высокоразрешающие фотографические среды) и создания оптических систем сверхразрешения на базе оптических микроскопов.

Реконструкция сигнала на основе прямого решения систем уравнений (1) требует больших вычислительных затрат. Поэтому восстановление промежуточных значений между отсчетами на основе преобразования Фурье является достаточно перспективным способом для разработки оптических систем с субпиксельным пространственным разрешением.