Повышение разрешающей способности генетических анализаторов при определении температуры плавления ДНК

Основной целью применения генетических анализаторов на основе метода ПЦР в реальном времени является качественный и количественный анализы ДНК, в результате которых обнаруживается искомый фрагмент ДНК и определяется его количество.

Основные особенности ПЦР заключаются в высокой избирательности и чувствительности, достигающей единиц целевых молекул ДНК. Основным метрологическим параметром ПЦР в реальном времени является величина порогового цикла С t . При количественных анализах на основе С t возможно определение относительных количеств молекул ДНК, например при анализах генетически модифицированных продуктов, или абсолютных количеств путем сравнения с известными калибровочными образцами.

Дополнительная информация может быть получена при использовании методики плавления ДНК. Эффект плавления ДНК (DNA melting) — процесс перехода регулярной двойной спирали линейной молекулы ДНК в клубкообразное состояние под действием температуры [1, 2].

Анализ кривых плавления в основном используется для определения температуры плавления Tm продуктов амплификации с применением интерка-лирующих красителей, праймеров и зондов. В реактивы ПЦР-реакции, ориентированной на целевую последовательность, добавляют минимум два олигонуклеотидных праймера. Праймеры следует подбирать таким образом, чтобы они имели близкие температуры плавления Tm. Если Tm прайме- ров отличаются, амплификация будет менее эффективной или может вовсе не сработать.

При использовании кривых плавления в системах с ДНК-зондами (Taq-man assay, molecular beacons) можно различить точечные мутации, расположенные внутри областей связывания ДНК-матрицы и зонда. Наличие таких мутаций способно привести к изменению температуры плавления зонда и к изменениям графика кривой плавления [3].

Зависимость температуры плавления ДНК от состава объясняется ее энергетическим состоянием: в паре гуанин—цитозин (G-C) три водородные связи, в паре аденин—тимин (А-Т) только две. Поэтому чем больше G-C в ДНК, тем более она "тугоплавка" [4].

Кривая плавления получается путем наблюдения интенсивности флуоресценции продуктов ПЦР при изменении температуры с шагом 0.5 или 1 °C. При вторичной обработке определяется температура плавления T m , которая зависит от длины и состава фрагмента ДНК.

В многочисленных литературных источниках [5–8] приведены формулы для вычисления температуры плавления T m праймеров и продуктов амплификации, в которых в явном виде выражена зависимость T m от длины фрагмента и процентного содержания суммы нуклеотидов C и G. Например, можно применить для вычисления T m заимствованную из статьи [5] формулу (1):

T m =

= 81.5 + 16.6 lg [K⁺] + 0.41 [G + C] % – 675 / L p , (1) где [K⁺] — концентрация ионов калия, моль;

[G + C] % — количество G и С в продукте ПЦР, %; L p — длина продукта, число пар нуклеотидов.

Из этой формулы следует, что изменение содержания суммы нуклеотидов C и G на 1 % вызывает изменение температуры плавления T _m на 0.41 °C. Поэтому естественно желание исследователей уменьшить погрешность измерения величины T m .

В настоящей статье рассмотрены основные причины погрешностей измерения T m и предложен способ их уменьшения.

СРАВНЕНИЕ СПОСОБОВ ОПРЕДЕЛЕНИЯ ПОРОГОВЫХ ЦИКЛОВ И ТЕМПЕРАТУРЫ ПЛАВЛЕНИЯ

При ПЦР-анализах динамическая кривая зависимости интенсивности флуоресценции от температурных циклов имеет S-образную форму и содержит три участка: участок экспоненциального роста, на котором наблюдается удвоение продукта при каждом цикле; участок максимального роста интенсивности сигналов флуоресценции и участок насыщения (плато), на котором реакция прекращается.

При вторичной обработке используются следующие основные методы расчета: кусочнолинейная аппроксимация по двум точкам и аппроксимация по нескольким точкам. Примером метода первой группы может служить метод порога (отсюда название параметра "пороговый цикл"). Примером аппроксимации по нескольким точкам может служить моделирование на базе монотонной нелинейной S-образной функции класса сигмоид. В статьях [9, 10] показано, что при использовании аппроксимации сигналов флуоресценции сигмоидальной функцией обеспечивается снижение погрешностей измерения порогового цикла.

Кривая плавления зондов имеет подобную форму, на среднем участке наблюдается максимальное изменение интенсивности флуоресценции. Рост интенсивности флуоресценции при плавлении зондов вызывается эффектом уменьшения влияния гасителя на флуоресцентный краситель. Кривая плавления образцов с неспецифическими красителями имеет обратную зависимость, при этом наблюдается значительный дрейф нулевой линии, который обусловлен температурными свойствами красителей.

Можно назвать следующие основные причины погрешностей измерения величины T m : погрешность дискретизации, шумы и дрейф нулевой линии.

Традиционно вычисление величины Tm обеспечивается путем дифференцирования и анализа производной кривой плавления. Однако при дифференцировании кривой плавления сигнал уменьшается, а шумы возрастают.

Поскольку кривая плавления носит ступенчатый характер (1 точка на дискретную единицу температуры, например 0.5 или 1 °C), то для повышения точности расчетов далее рассматривается возможность определения температуры плавления ДНК путем аппроксимации кривой плавления сигмоидальной функцией. В отличие от традиционной методики вычисления величины T m при аппроксимации сигмоидальной функцией дифференцирования кривой плавления не требуется.

Преимущества аппроксимации сигмоидальной функцией можно объяснить ее способностью значительно уменьшить влияние на погрешность измерения дискретизации входных данных, шумов и дрейфа нулевой линии.

АНАЛИТИЧЕСКАЯ ФОРМА СИГМОИДАЛЬНОЙ ФУНКЦИИ

Усовершенствованную модель кривой плавления на базе нелинейной сигмоидальной функции (СФ) предлагается выразить в виде формулы (2), приведенной в работе [11]:

F с = F m / (1 + exp (( T m – T ) / k )) +

+ f 0 + f 1 · T + f 2 · T ²,                     (2)

где Fс — относительная величина интенсивности флуоресценции при температуре образца T (°C); Fm — относительная интенсивность (размах) участка плавления; Tm — дробное значение температуры плавления (°C); k — коэффициент, который определяется наклоном кривой; слагаемые f0 + f1 · T + f2· T2

учитывают смещение, а также линейную и квадратичную зависимости нулевой линии от температуры.

МЕТОДИКА ПОСТРОЕНИЯ И ОПТИМИЗАЦИИ ПАРАМЕТРОВ СФ КРИВОЙ ПЛАВЛЕНИЯ.

ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ПЛАВЛЕНИЯ

Исходные (сырые) данные кривой плавления получены на анализаторе нуклеиновых кислот АНК-32, который серийно выпускается в Институте аналитического приборостроения РАН (ИАП РАН). Использовались образцы мРНК NAP-22, приготовленные по методике, описанной в работе [12].

Полный фрагмент NAP-22 приведен в базе данных нуклеотидных последовательностей [13].

Ограниченный фрагмент NAP-22 длиной 1209 нуклеотидов получен согласно протоколу ПЦР-РВ с обратной транскрипцией [14] с помощью следующих праймеров и зонда:

– NAP-22_up                    aac-tcc-aag-atg-gga-agc-aag  ("верхний" праймер для ПЦР-РВ);

– NAP-22_low                    cag-cct-tct-tgt-ctt-tdt-cct-t    ("нижний" праймер для ПЦР-РВ);

– oligo dT(15)-T7 primer:

(5! AAA CGA CGG CCA GTG AAT TGT AAT ACG ACT CAC TAT AGG CGC T(15) 3!) [57-mer] (праймер для обратной транскрипции);

– NAP-22_Pr_up_R           (ROX)ct-aca-atg-tga-acg-acg-aga-agg-cca-(RTQ2) (зонд в канале ROX).

На рисунке приведены графики исходных кривых плавления двух одинаковых проб, полученных после ПЦР, и кривые плавления СФ с оптимизированными параметрами. Эти графики отражают зависимости интенсивности флуоресценции F и F с от температуры Т , приведенные в табл. 1. Можно отметить хорошее совпадение этих графиков.

В двух столбцах табл. 1 приведены значения температуры Т в диапазоне от 61 до 90 °C и соответствующие относительные значения интенсивности флуоресценции F пробы 1. В третьем столбце табл. 1 приведены значения флуоресценции Fс, вычисленные по формуле (2). В следующем столбце — квадраты отклонений Dс = (F – Fc)2, а в целевой последней ячейке — сумма S квадратов отклонений. Нахождение параметров СФ выполняется в программе Excel средством анализа Поиск решения из меню Данные, при этом определяется минимальное значение величины S путем из- менения параметров СФ.

Далее приведена более подробная последовательность получения оптимизированных параметров СФ с помощью электронной таблицы Excel.

• 1)    Нулевая линия аппроксимируется полиномом f 0 + f 1 · T на начальном участке исходной кривой плавления (61–65 °C). В результате определяются приблизительные параметры f 0 и f 1 .

• 2)    Полная последовательность по диапазону (61–90 °C) аппроксимируется СФ согласно формуле (2). При этом для учета обратной зависимости флуоресценции от температуры первое слагаемое в формуле (2) используется со знаком минус. Определяются приблизительные параметры F m , T m , k и f 2 , не изменяя параметры f 0 и f 1 .

• 3)    Повторно полная последовательность (61– 90 °C) аппроксимируется СФ. При этом оптимизируются все параметры СФ.

  
  
  

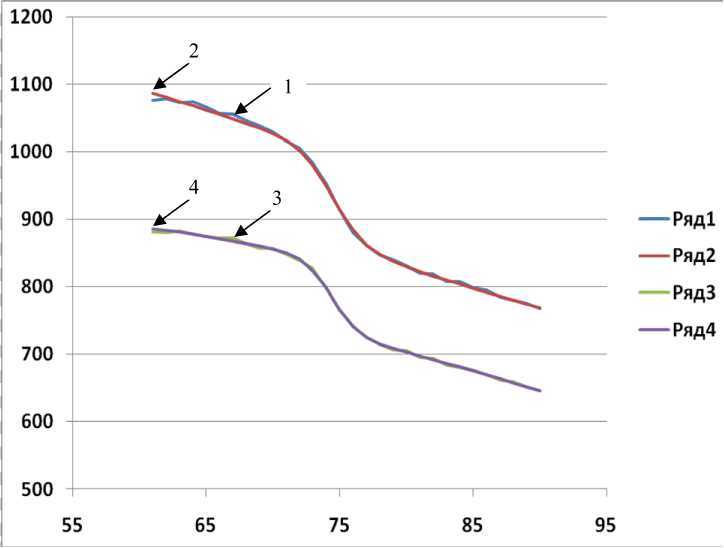
  Исходные данные кривых плавления двух проб.

  Ряды 1 и 3 — экспериментальные кривые с шумом; СФ с оптимизированными параметрами — ряды 2 и 4, гладкие кривые.

  Вертикальная ось — относительная величина интенсивности флуоресценции; горизонтальная ось — температура образцов (°C)

  
  

Табл. 1. Оптимизация параметров СФ

Т , °C	F	F с	D с	S
61	894.23	880.67	183.91	704.99
62	889.36	880.33	81.52	–
63	884.51	882.67	3.41	–
64	879.68	877.67	4.05	–
65	874.86	874.00	0.74	–
86	670.99	670.33	0.43	—
87	666.56	661.33	27.29	–
88	662.14	659.33	7.89	—
89	657.74	651.00	45.47	–
90	653.36	645.67	59.23	—

Табл. 2. Результаты вычисления параметров СФ

Пробы	Параметры СФ	Значения
1	T m1	74.50
	F m	141.88
	k	1.22
	f 0	1507.75
	f 1	–7.44
	f 2	0.009
2	T m2	74.44
1, 2	T m1 – T m2	0.06

В табл. 2 приведены оптимизированные значения параметров СФ для одинаковых проб в двух смежных пробирках 1 и 2.

Основными результатами применения СФ являются определенные величины температуры плавления T m1 = 74.50 и T m2 = 74.44 °C. С целью сравнения полученных результатов в последней строке таблицы вычислены значения разности температур плавления T m1 – T m2 = 0.06 °C. Разность температур плавления можно объяснить градиентом температур держателя соседних пробирок.

ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ПЛАВЛЕНИЯ ПРИ ИСПОЛЬЗОВАНИИ ПРОГРАММЫ MATLAB

Предложенная методика СФ реализована также путем использования программы MATLAB.

СФ задается на языке пакета в виде формулы (3):

f = @(x,u) (-x(2)./(1+exp((x(1)-u)./x(3)))) + x(4) +

+ x(5)*u + x(6)*u.^2 , (3)

где x(1) , …, x(6) соответствуют параметрам T m , F m , k , f 0 , f 1 и f 2 в формуле (2).

Использованы следующие команды MATLAB:

x0 = [74 141 1 1500 -7 0.009] — задаются приблизительные значения параметров;

x = lsqcurvefit(f,x0,s,V) — новые значения параметров. Здесь исходные данные s и V — значения температуры и интенсивности флуоресценции (ранее обозначенные как Т и F );

Vn = f(x,s) — новые значения данных;

plot(s,V,'ob') — печать исходных данных;

plot(s,Vn,':r') — печать новых данных;

legend('Данные','Апроксимация',2) — надписи на графиках;

ds = sum((V-Vn).^2) — сумма квадратов отклонений, может быть использована для сравнения качества оптимизации;

Команды программы MATLAB могут быть сохранены в виде M-файла, при этом расчет температуры плавления может выполняться в автоматическом режиме.

ЗАКЛЮЧЕНИЕ

Предложена усовершенствованная модель аппроксимации кривой плавления ДНК и методика оптимизации ее параметров на основе одного из наиболее эффективных способов обработки сигналов — способа аппроксимации с помощью сигмоидальной функции (СФ).

Основным результатом применения СФ является определение величины температуры плавления ДНК T m .

При использовании предлагаемой методики аппроксимируется непосредственно кривая плавления, построения производной от кривой плавления не требуется.

Результаты применения СФ представлены в графическом виде.

Показана возможность полной автоматизации вычислений для определения температуры плавления ДНК.