Повышение разрешающей способности радиолокатора по дальности за счет инверсной фильтрации

В современной радиотехнике актуальна задача оценки параметров и обработки сигналов в многосигнальной ситуации [1]. Это повышает требования к разрешающей способности измерителя до значений, превосходящих «рэлеевский предел» [2]. Известными подходами, реализующими «сверхрэлеевское» разрешение в радиолокации, являются методы современного спектрального оценивания [3, 4], многоканального анализа [5, 6], проекционной теории [7] и др. [8]. Применение этих методов ограничено известными недостатками, например, для каждого метода в различной комбинации сочетаются требования к наличию априорной информации (знание количества сигналов или их координат и др.), значительные потребные вычислительные затраты, недостаточная устойчивость получаемых оценок.

Согласно [9] разрешение сигналов можно считать частной задачей апостериорного восстановления сигналов. Одним из широко применяемых методов восстановления искаженных сигналов в подповерхностной радиолокации при разделении суммы двух перекрывающихся во времени импульсов схожей формы [10] и в оптике при повышении контрастности изображений [11] является инверсная фильтрация.

Несмотря на то что на базе инверсного фильтра эффективно решается задача разрешения [12], в радиолокации инверсная фильтрация достаточного распространения не получила. Причина этого заключается в том, что без дополнительных мер по выделению сигнала на фоне шума инверсная фильтрация может применяться только при отношении сигнал-шум (ОСШ) от 30 дБ (здесь и далее приводятся оценки ОСШ относительно пикового значения сигнала на выходе согласованного фильтра). Это обусловлено тем, что спектр зондирующего сигнала (из – 302 – которого, как будет показано ниже, можно определить частотную характеристику инверсного фильтра) на некоторых частотах принимает нулевые или близкие к нулевым значения. В результате коэффициент передачи инверсного фильтра на этих частотах в пределе стремится к бесконечности. Последнее приводит к усилению спектральных составляющих шума и снижению качества результата обработки [9, 13, 14]. Задача разрешения с помощью инверсной фильтрации в этом случае становится некорректной.

Решение некорректной задачи можно регуляризировать, приняв меры к исключению источников локальных шумов выходного сигнала. Очевидным подходом к исключению таких источников шумов является коррекция частотной характеристики инверсного фильтра на частотах, где она принимает близкие к нулевым значения.

Исходя из того что в известных работах по инверсной фильтрации [15, 16] рассматривается обработка сигналов, рассогласованных по времени, для примера рассмотрим повышение разрешающей способности радиолокатора по дальности. Для исключения влияния на результат обработки особенностей структуры сигнала в качестве зондирующего примем импульсный сигнал типа «простой радиоимпульс». На данном этапе исследований положим, что принятые сигналы не различаются по частоте.

Таким образом, в статье предлагается рассмотреть повышение разрешающей способности радиолокатора по дальности с импульсным сигналом типа «простой радиоимпульс» за счет инверсной фильтрации с регуляризацией.

Инверсная фильтрация перекрывающихся по дальности простых радиоимпульсов

Для аналитического описания процесса инверсной фильтрации воспользуемся математическим аппаратом, предложенным в [5], и рассмотрим обработку дискретного импульсного сигнала, отраженного от групповой цели, образованной M -точечными источниками вторичного излучения (рис. 1).

I й sm

I u s

| u s 2

| u* s 1

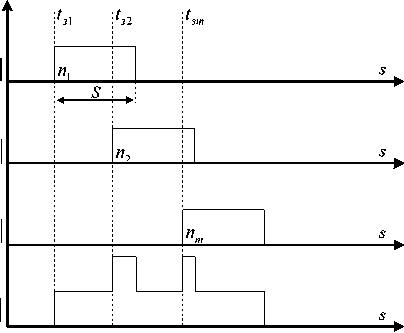
Рис. 1. Импульсный сигнал, отраженный от групповой цели, образованной M -точечными источниками вторичного излучения

Fig. 1. Pulse signal reflected from a group target formed by M -point local sources of secondary radiation

Пусть на входе схемы обработки наблюдается сигнал, описываемый выражением

M

Us = g <0's'T-'m ’. nm ^ s < n. ■ S, где am - амплитуда m-го импульса; f0 - частота сигнала; 5 - номер дискретного отсчета; AT -интервал дискретизации; t3m — время запаздывания m —го импульса; n. = ]^/АT[ - номер дискретного отсчета, которому соответствует фронт m-го импульса; А - число отсчетов в импульсе. Обозначим нормированную к интервалу дискретизации частоту, выраженную в долях ширины фильтра, как относительную частоту X = f0АTN и запишем выражение, описывающее спектр U* принятого сигнала

П т ⁺ ^ M    -^ _sn П т + S —               ₍ 2Л ( X - _n ) s

U n = УУ u s e N = УУ a m e 'f 0 t' e N ( ) ,° ^ n <  N -

S = П т m =1                  S = П т m =1

Применим к (1) соотношение для суммы членов геометрической прогрессии, где за член

2П(X-nn прогрессии принят q = e N    . Тогда данное выражение 1м ожно при вести к виду п/-2л

•       j —( S -1)( X—n )    / х х—1 -   - j—n_n

U n = e N ^{(  )(}    ) F n ( X ) Z a m e ^N m ,

– значение амплитудно-

m =1

Г .             j V Xnm.

где a;m = ame-2nf°t3me N ; F„(X) = sm частотной характеристики фильтра дискретного преобразования Фурье (ДПФ) с номером n на v                                                   -2nfoSДT A / / cc частоте X. Если к копии зондирующего сигнала u, = eJ °"  , 0 < s < S применить преобразо- s вание (1), то получим спектр ожидаем ого сигнала

:       j—( s-1)( x - n),

Un = eN )(   ' F. (X), из которого определим частотную характеристику инверсного фильтра

А

U - n

I -( S -1 )( X - n) /

N "  7 F n ( X ) .

Перемножение спектра сигнала (2) с частотной характеристикой инверсного фильтра (3) позволяет рассчитать спектр сигнала на выходе инверсного фильтра:

M

U J = и I I ^{- 1} = У <7 e ^{n n n} ^ ^m

2n j nn Nm.

m =1

Выражение (4) представляет собой сумму гармонических сигналов. Частоты этих колебаний определяются номерами дискрет дальности n ; m , в которых начинаются сигналы каждого из тт

M импульсов. Поскольку величины nm и n являются целыми числами, то это свидетельствует об ортогональности сигналов всех M-источников друг другу, прошедших обработку в инверсном фильтре [17, 18]. Очевидно, что обработка спектра сигнала в инверсном фильтре вида (4) приводит к тому, что модуль спектра преобразуется в прямоугольную форму на интервале – 304 – частот от 0 до N–1. Обратное БПФ над последовательностью (4) приведет к формированию на оси дальности отдельных пиков с амплитудами am в дискретах с номерами nm и нулей во всех остальных дискретах. Потенциальный интервал разрешения в рассматриваемых условиях определяется интервалом ΔT. Однако при наличии на входе схемы обработки шума на часто- тах, на которых значение sin

или близко к нулю, спектральные составляю- щие шума претерпят значительное усиление – в результате при ОСШ ниже 30 дБ правильное разрешение сигналов станет маловероятным.

Инверсная фильтрация с регуляризацией

Пусть относительно спектра ожидаемого сигнала выбран некоторый порог ν (рис. 2). В процессе инверсной фильтрации участвует та часть спектра, которая находится выше значения порога ограничения ν , т.е. частотная характеристика инверсного фильтра сформирована таким образом, что спектральные составляющие входного сигнала, соответствующие частотам, расположенным ниже порога из обработки, исключаются.

Тогда в обработке инверсным фильтром следует учитывать спектральные составляющие у сигнала Un , принадлежащие окрестностям частот, соответствующих L – лепесткам спектра зондирующего сигнала, превысившим порог.

Введем следующие обозначения: каждый l -й лепесток, превысивший порог, содержит k l спектральных составляющих и в каждом из l лепестков имеется спектральная составляющая n_l , соответствующая начальному номеру спектральной составляющей l -го лепестка. Учитывая введенные обозначения, отклик инверсного фильтра во временной области при регуляризации получим обратным дискретным преобразованием Фурье от выражения (4) с соответствующим ограничением пределов интегрирования (здесь суммирования):

L п_; + к        2п

1     j—ns us = £ Е Une   , 0 - s < Nl.

l =1 n = n

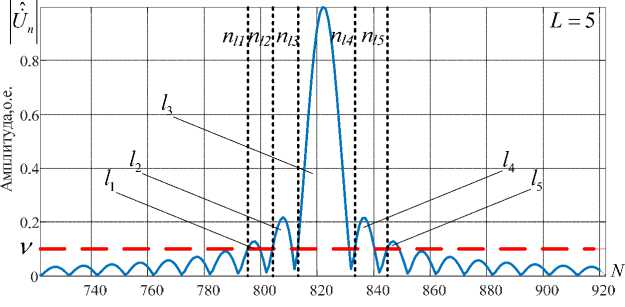
Рис. 2. Спектр зондирующего сигнала и порог ограничения ν = 0,1

Fig. 2. Spectrum of probing signal and limiting threshold ν = 0,1

Раскрыв (6) как сумму членов геометрической прогрессии, получим us где

F

, ;.-.

Из анализа выражения (7) следует: величины F_s ( n m ) максимальны при s = n m ; ширина главного лепестка F s ( n m ) зависит от числа спектральных составляющих k l . Таким образом, огибающая сжатого сигнала каждого из М точечных источников будет представлять собой сумму величин F s ( n m ) , умноженных на соответствующие амплитуды, и иметь главный и боковые лепестки на оси дальности.

На рис. 3 показана амплитудно-частотная характеристика инверсного фильтра, на рис. 4 – огибающая спектра сигнала с выхода инверсного фильтра. Фазочастотная характеристика инверсного фильтра совпадает с фазочастотной характеристикой согласованного фильтра.

На рис. 3 видно, что частотная характеристика инверсного фильтра при регуляризации режектирует частоты, на которых спектр зондирующего сигнала близок к нулю. При этом чем выше порог ограничения, тем с большим превосходством над шумовыми составляющими отбираются фильтром спектральные составляющие сигнала и тем выше должна обеспечиваться вероятность правильного разрешения. Однако исключение из обработки части составляющих спектра сигнала приводит к расширению отклика инверсного фильтра во временной области. Эту особенность можно пояснить анализом рис. 4.

Модуль спектра отклика инверсного фильтра близок по форме к последовательности прямоугольных импульсов, протяженность которых при повышении уровня ограничения уменьшается, а при уменьшении – увеличивается. Соответственно, при переходе во временную область повышение порога ограничения приводит к расширению отклика инверсного фильтра,

M

L

= 2 a m F_s ( П т ) 2

т =1

l =1

j^s ^- n m )( n l ^- k l ^{- 1} ) e_N m _,

sin

( Пт )=-

.

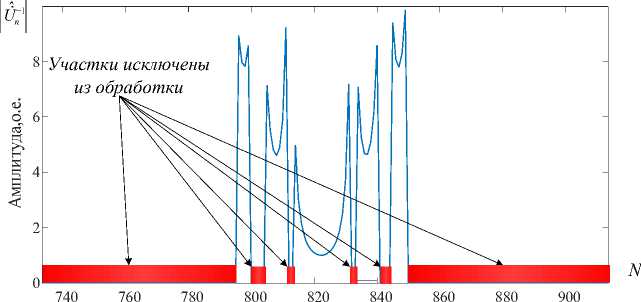
Рис. 3. Частотная характеристика инверсного фильтра

Fig. 3. Frequency response of inverse filter

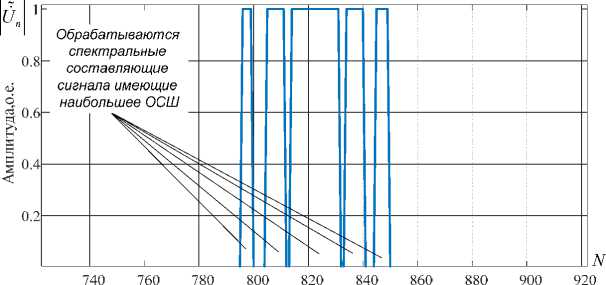
Рис. 4. Спектр отклика инверсного фильтра

Fig. 4. Spectrum response of inverse filter

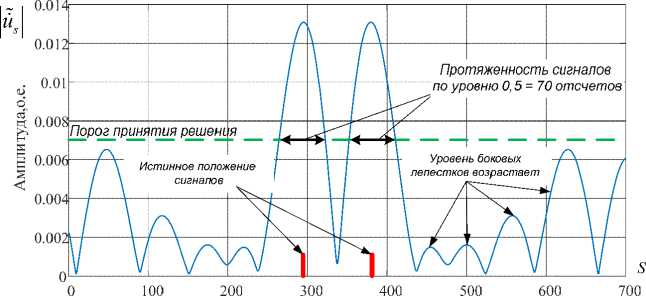
Рис. 5. Отклик инверсного фильтра во временной области

Fig. 5. Temporal response of inverse filter при уменьшении – к сужению. Таким образом, выбор порога ограничения или значения параметра регуляризации инверсной фильтрации является отдельной задачей, влияющей на качество разрешения сигналов.

На рис. 5 представлен отклик инверсного фильтра, отраженного от двух локальных равноамплитудных источников вторичного излучения, удаленных друг от друга по дальности на 0,25 интервала разрешения по Рэлею.

На рис. 5 видно, что отклик инверсного фильтра уже не определяется интервалом дискретизации Δ T , что наблюдалось при инверсной фильтрации без регуляризации. Вторым негативным фактором предложенной регуляризации можно считать появление боковых лепестков. Однако регулярный характер роста уровня боковых лепестков влево и вправо относительно положения обнаруженных сигналов позволяет разработать различные способы борьбы с ними.

С учетом того, что относительно задачи обнаружения оптимальна согласованная обработка, инверсную фильтрацию следует применять после факта обнаружения сигнала. При этом для борьбы с боковыми лепестками можно использовать в качестве взвешивающей функции отклик согласованного фильтра, который будет спадать влево и вправо от обнаруженного сигнала. Последним фактором, усложняющим применение инверсной фильтрации с регуляризацией, является выбор значения параметра регуляризации (порога ограничения спектра зондирующего сигнала). Ниже предлагается эмпирически полученный алгоритм выбора этого значения.

Алгоритм выбора значения параметра регуляризации инверсной фильтрации

Значение параметра регуляризации должно изменяться ступенчато согласно количеству спектральных составляющих, подвергающихся обработке при данном уровне ограничения спектра зондирующего сигнала. Однако улучшение качества разрешения при таком строгом выборе значения параметра регуляризации незначительно и не оправдывает затраты на его вычисление. Поэтому предположим, что справедлива гипотеза о допустимости линейной зависимости значения параметра регуляризации от ОСШ.

Для описания линейного закона изменения параметра регуляризации необходимо задаться двумя точками. Точки выберем исходя из практической целесообразности применения инверсной фильтрации. Исследования показали, что инверсная фильтрация с регуляризацией применима при ОСШ от 18 до 30 дБ [16]. При более низких ОСШ регуляризация не обеспечивает достаточного качества результатов обработки, при более высоких – оптимальное значение параметра регуляризации близко к нулю.

Согласно [19] при решении задачи разрешения парной цели допускается уровень ложной тревоги F ≤ 0,05, поэтому требуется определить требуемое значение параметра регуляризации при указанных ОСШ, обеспечивающих уровень ложной тревоги не более 0,05. Для примера рассмотрим систему обработки одиночного сигнала с параметрами: ширина спектра сигнала 20 Гц, длительность импульса 0,1 с, частота 5 МГц, тип сигнала – простой радиоимпульс.

Подберем эмпирически значение порога ограничения ν1 при ОСШ, равном 18 дБ, обеспечивающее уровень ложных тревог F ≤ 0,05. Значение порога ограничения при выбранных параметрах сигнала составляет 0,22 от максимального значения спектра зондирующего сигнала. На практике в большинстве случаев это соответствует уровню первых боковых лепестков спектра зондирующего сигнала. Также требуется подобрать значение порога ограничения ν2 при ОСШ, равном 30 дБ, обеспечивающее уровень ложных тревог F ≤ 0,05. В этом случае значение порога ограничения составляет 0,04 от максимального значения спектра зондирующего сигнала.

Выбранные значения порога ограничения при ОСШ 18 и 30 дБ позволяют определить зависимость уровня порога ограничения от ОСШ (рис. 6). По выдвинутой гипотезе точки v1 ( xl; y l) и v2 (x 2 ; y2) принадлежат одной прямой, следовательно, координаты этих точек x, у удовлетворяют уравнению вида y = kx + b . Переменная y соответствует значению уровня порога ограничения, переменная x – значению ОСШ, т. е. справедливы равенства, образующие систему уравнений вида

• У 1 = kx 1 + b

  
  

• У 2 = kx 2 + b

Рассчитав из системы уравнений (8) коэффициенты k = ——— и b = y 1 - y ²—— x 1 , мож- x 2 - x 1              x 2 ^— x 1

но определить значение порога регуляризации при наблюдаемом ОСШ. Так, для рассматриваемого примера уравнение определения значения параметра регуляризации будет иметь вид y = –0,015 x + 0,49. На рис. 6–8 представлена сравнительная оценка инверсной фильтрации без регуляризации и с регуляризацией, полученных имитационным моделированием. Значения параметра регуляризации выбиралось согласно предоженному алгоритму. В качестве предельного относительного интервала разрешения принят предел Хелстрома [7].

На рис. 7–9 видно, что повышение разрешающей способности радиолокатора инверсной фильтрацией с регуляризацией (пунктирная линия) в несколько раз превосходит инверсную фильтрацию без регуляризации (точечная линия) по разрешению и обладает достаточными вероятностями правильного разрешения при ОСШ от 18–25 дБ и более.

Заключение

В статье показано применение инверсной фильтрации с регуляризацией для повышения разрешающей способности радиолокатора с простым радиоимпульсом по дальности. В ка-

Рис. 6. Зависимость значения параметра регуляризации от ОСШ

Fig. 6. Dependence of the value of limiting threshold by signal-to-noise

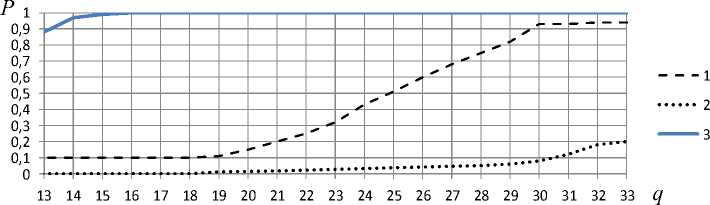
Рис. 7. Зависимость вероятности правильного разрешения двух целей, удаленных друг от друга по дальности на 0,1 интервала разрешения по Рэлею: 1 – инверсная фильтрация с регуляризацией; 2 – инверсная фильтрация без регуляризации; 3 – предельный относительный интервал разрешения

Fig. 7. Dependence of the probability of correct resolution of two impulse, remoted in range by 0.1 of the Rayleigh resolution interval: 1 – inverse filtering method with regularization; 2 – inverse filtering without regularization; 3 – limiting relative resolution interval

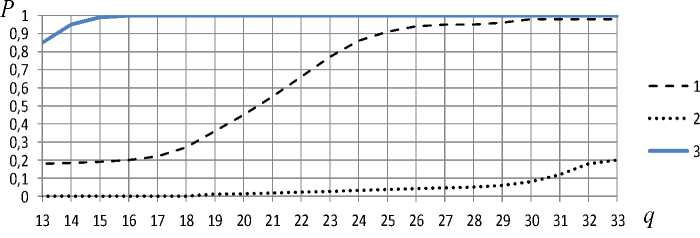
Рис. 8. Зависимость вероятности правильного разрешения двух целей, удаленных друг от друга по дальности на 0,25 интервала разрешения по Рэлею: 1 – инверсная фильтрация с регуляризацией; 2 – инверсная фильтрация без регуляризации; 3 – предельный относительный интервал разрешения

Fig. 8. Dependence of the probability of correct resolution of two impulse, remoted in range by 0.25 of the Rayleigh resolution interval: 1 – inverse filtering method with regularization; 2 – inverse filtering without regularization; 3 – limiting relative resolution interval

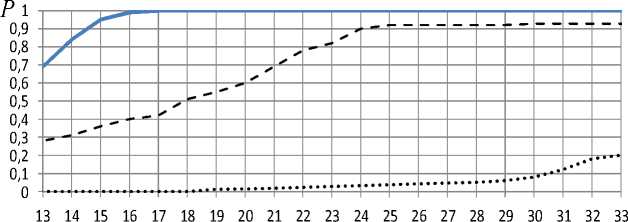
^^^^^^ 3

Рис. 9. Зависимость вероятности правильного разрешения трех целей, удаленных друг от друга по дальности на 0,5 интервала разрешения по Рэлею: 1 – инверсная фильтрация с регуляризацией; 2 – инверсная фильтрация без регуляризации; 3 – предельный относительный интервал разрешения

Fig. 9. Dependence of the probability of correct resolution of two impulse, remoted in range by 0.5 of the Rayleigh resolution interval: 1 – inverse filtering method with regularization; 2 – inverse filtering without regularization; 3 – limiting relative resolution interval честве параметра регуляризации выбран порог ограничения спектра зондирующего сигнала. Наиболее сложной задачей регуляризации является выбор значения порога ограничения. При некоторых допущениях это можно делать на основании эмпирически полученных зависимостей. Предложенный подход позволяет повысить разрешающую способность радиолокатора по дальности не менее чем в четыре раза при ОСШ от 18–25 дБ.