Повышение скорости выполнения операции модульного возведения в степень многоразрядных чисел

Червяков Н.И., Лобес М.В.

В статье рассмотрен алгоритм Монтгомери ускоренного модульного умножения многоразрядных чисел. Предложено адаптировать его для системы остаточных классов. Показано, что такая модификация алгоритма Монтгомери дает огромное преимущество по времени выполнения операции модульного умножения, а, следовательно, и операции модульного возведения в степень.

Постановка задачи

В последние годы наблюдается повышенный интерес к методам и алгоритмам теории чисел, сложность реализации которых во многом зависит от входящих в них арифметических операций. Большинство из известных теоретико-числовых методов и алгоритмов содержат неоднократное выполнение операции модульного возведения в степень. При этом области, в которых эти методы и алгоритмы применяются, требуют обработки многоразрядных чисел [1]. Трудность состоит в том, что в рамках производительности современных вычислительных устройств, функционирующих в позиционной системе, реализация операции модульного возведения в степень многоразрядных чисел становится достаточно трудоемкой. Это объясняется необходимостью учета межразрядных переносов. Поэтому для того, чтобы значительно повысить производительность вычислительных устройств необходимо применение систем счисления, лишенных подобного недостатка [2].

В свете сказанного актуален переход к непозиционным системам счисления, наиболее перспективной из которых является система остаточных классов. Эта система обладает множеством неоспоримых преимуществ, в сравнении с позиционной системой, однако ее широкое применение сдерживается рядом причин [3].Одна из них состоит в том, что при обработке многоразрядных чисел определенные трудности возникают при выполнении такой операции как модульное возведение в степень. Следовательно, для построения полноценной компьютерной арифметики на базе системы остаточных классов необходимо разработать эффективный алгоритм выполнения этой операции.

Адаптация алгоритма ускоренного модульного умножения Монтгомери для системы остаточных классов

Так как классический алгоритм модульного возведения в степень сводится к ряду модульных умножений, то главным вопросом является разработка эффективного метода и алгоритма для выполнения этой операции. Трудность заключается в том, что операция модульного умножения по произвольному модулю предполагает реализацию операции деления, которая является достаточно сложной в любой, в том числе и в позиционной системе.

Одним из самых эффективных алгоритмов, известных в литературе и применяемых для ускорения операции модульного умножения, является алгоритм Монтгомери, основная идея которого заключается в преобразовании операндов в некоторые остатки и вычислении произведения этих остатков. Полученный результат умножения преобразуется назад к нормальному виду [4]. Такой подход выгоден, если необходимо вычислить ряд умножений в преобразованной сфере. Преимущество алгоритма Монтгомери состоит в том, что операция модульного умножения по произвольному модулю с помощью определенных преобразований заменяется рядом сложений и умножений по модулю, представляющему собой степень двойки. При этом трудоемкая операция деления заменяется несколькими битовыми операциями сдвига. Для того чтобы алгоритм Монтгомери подходил для практической реализации, удобнее всего выбрать двоичную систему счисления (см. рис. 1).

Результат модульного умножения после применения алгоритма получается в виде S m + 1 = ABR ^-1 mod M . Для того, чтобы привести его к нормальному виду нужно применить преобразование Монтгомери [4].

Так как алгоритм Монтгомери применяется в позиционной системе счисления, то, несмотря на преимущества, его применение не дает скачкообразного повышения скорости выполнения операции модульного умножения.

В алгоритме Монтгомери на каждом шаге используется младший коэффициент позиционного представления для вычисления q i . Поэтому он может быть адаптирован для системы остаточных классов (см. рис. 2), если использовать обобщенную позиционную систему с аналогичным набором оснований. Пусть p i , Р 2 ,..., pk - основания системы остаточных классов и R = p i • Р2 • ... • pk диапазон.

Алгоритм Монтгомери, адаптированный для системы остаточных классов, вычисляет значение S так что

На каждом этапе алгоритма вычисляется цифра обобщенной позиционной системы

q i = |si + a i bi |

p _i

p i - m i

p _i

pi и цифры представления в системе остаточных классов

s j

s j ⁺ ai b j ⁺ qi

m j

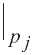
1 p i _{p j}

S ≡ ABR ^-1 modM .           (1)

. (3)

^p j

( Начало ) ___________________ t ____________________ 'Ввод : в = 2 — основание системы счисления;

a и b - операнды модульного умножения;

M = m o + m i ■ 2 + ... + m m ■ 2 ^m , m i e { 0,1 } , ( 2, M ) = 1 - двоичное представление модуля ;

M <  R = 2 ^m - модуль алгоритма Монтгомери;

A = a ■ R mod M и B = b ■ R mod M - операнды после преобразования Монтгомери;

A, B <  M ; A = a o + a i ■ 2 + ... + a m ■ 2 , a i e { 0,1 } — двоичное представление .

S о : = 0

-----------------><=! := 0, m,K>------------- qi := (Si + ai • B)mod 2

^Si+1 ^:= (Si ⁺ qi " M ⁺ ai "^B)/²

___________________________________________________________________________________________________________________________________________________________I

___________ *

Вывод : S _m+1

( Конец )

Рис. 1. Алгоритм Монтгомери для двоичной системы счисления

При этом значения s _j вычисляются таким образом, что они являются кратными p j .

Следовательно, если основания системы являются простыми числами, то деление s j на p j заменяется умножением на мультипликативную обратную величину.

Тогда из алгоритма имеем равенство

• aiB + qiM

• —----¹--+ a2 B + q2 M

  ----P1 ----------------⁺ •. ⁺ ak — IB ⁺ qk — IM

S =--------- p2 --(4)

^p k -1

Равенство (4) после приведения к общему знаменателю и группировки имеет вид

^S = ^^{(( a} 1 ⁺ a 2 P i ⁺ ... ⁺ a k P i ... P k - I ) R

B +

или

S = R ( A • B + Q • M ) .

Следовательно, так как

Q • M mod M = 0 , (7) то справедливо сравнение (1).

Кроме этого на каждом этапе алгоритма с помощью операции расширения системы оснований вычисляется остаток s i- по основанию P i . Для определения цифры s i по основанию P i предложен метод расширения системы оснований на основе представления ортогональных базисов в обобщенной позиционной системе.

На основе алгоритма Монтгомери, адаптированного для системы остаточных классов, и классического алгоритма модульного возведения в степень может быть разработан алгоритм модульного возведения в степень многоразрядных чисел. Для этого результат каждого модульного умножения необходимо использовать как один или оба (в случае возведения в квадрат) операнда последующего модульного умножения.

( Начало ) ____________________ w _________________________

'Ввод : А и В - операнды модульного умножения;

р_х, Ру,..., р_к — основания системы остаточных классов;

R = рх • р, •... • рк — диапазон;

А = ах + а, • рх + ак • рх -ру + ... + ак ■ рх • р, •...• рк_х — представлтиев обобщенной позиционной системе счисления;

В = (bx,by,...,bk), bx = |S|^ , i е {1,2,..., £} — представление в системе остаточных / классов;/

М - модуль, (М, R) = 1, 0 < М<Ф'РАХ/

М = ^тх,ту,...,тк), тх =|Л/|^ , i е\\,Т,...,к\ - представление в системе / остаточных классов/

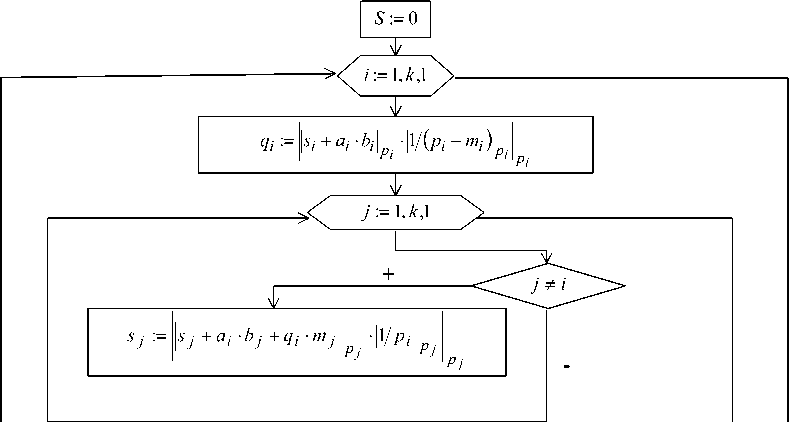
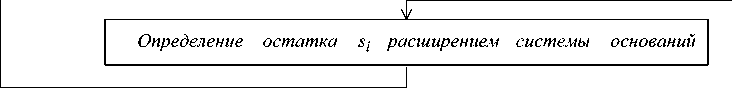
Вывод : S 7

\1/

Конец )

Рис. 2. Алгоритм Монтгомери, адаптированный для системы остаточных классов

Сравнительная оценка основного алгоритма Монтгомери,адаптированного для системы остаточных классов

Преобразование Монтгомери, выполняемое в начале и в конце алгоритма, может не оценивать-ся,так его сложность при большом количестве модульных умножений практически не влияет на преимущество, даваемое непосредственно алгоритмом Монтгомери.Так же можно не оценивать преобразования операндов и результата из позиционной системы в систему остаточных классов и обратно, так как разработанный алгоритм модульного умножения рассчитан на применение в специализированном вычислительном устройстве, целиком работающем в системе остаточных классов.

Сравнительная оценка может быть выполнена по двум критериям: по общему количеству битовых операций, выполняемых в алгоритме и по количеству битовых операций, определяющих время реализации алгоритма.

Оценка общего количества битовых операций, выполняемых в алгоритмах в зависимости от разрядностей операндов (см. таблицу 1), показывает, что основной алгоритм Монтгомери содержит в среднем в 1,2 раза меньше битовых операций.

Таблица 1. Оценка общего количества битовых операций алгоритмов

Разрядность операндов	Общее число битовых операций, выполняемых в алгоритме		≈⎜⎜⎛O M+С ⎟⎟⎞ ⎝ O M ⎠
	Монтгомери (O m )	Монтгомери + СОК ( O M + c )
8	208	310	1,5
16	800	1128	1,4
32	3136	3896	1,2
64	12416	13640	1,1
128	49408	54928	1,1
256	197120	217964	1,1
512	787456	856304	1,1
1024	3147776	3374377	1,1

Оценка количества битовых операций, определяющих время реализации алгоритмов (см. таблицу 2) показывает, что применение алгоритма Монтгомери, адаптированного для системы оста- точных классов, дает огромное преимущество по времени выполнения операции модульного умножения, причем оно возрастает с ростом разрядностей операндов.

Таблица 2. Оценка количества битовых операций, определяющих время реализации алгоритмов

Разрядность операндов	Число битовых операций , определяющих время реализации алгоритма		≈ ⎜⎛ O M ⎟⎞
	Монтгомери (O m )	Монтгомери + СОК ( O M + c )	⎜ ⎝ OM′ + C ⎟ ⎠
8	208	256	0,8
16	800	739	1,1
32	3136	1658	1,9
64	12416	3839	3,2
128	49408	10852	4,6
256	197120	31167	6,3
512	787456	89572	8,8
1024	3147776	269236	11,7

Выводы

Сравнительная оценка показала, что по вычислительной сложности (количеству битовых операций) алгоритм Монтгомери, адаптированный для системы остаточных классов, незначительно уступает основному алгоритму Монтгомери. Однако за счет малой разрядности оснований систе- мы остаточных классов и параллельной структуры вычислений разработанный метод и алгоритм дает существенный выигрыш по времени реализации операции модульного умножения, причем этот выигрыш растет с ростом разрядностей операндов.

Применение алгоритма Монтгомери, адаптированного для системы остаточных классов, позволяет время выполнения операции модульного воз- ведения в степень 1024 разрядными операндами уменьшить в 17,5 раз.