Повышение сопротивленияусталости за счёт формирования остаточных напряжений при нарезании резьбы сультразвуком

ных по направлению вынужденных ультразвуковых колебаний, на предельную амплитуду цикла.

Экспериментальные результаты могут быть обработаны по этому методу с ис-пользованием соотношения вида:

О" = О" , —(/(ст   +<7 )

a - 1 т ' ост m ^, где v — феноменологический параметр; ст а -предельная амплитуда цикла; ст _т - среднее растягивающее напряжение; ст _ост - остаточные напряжения.

Однако для установления связи между остаточными напряжениями и сопротивлением усталости необходимо учесть следующие факторы:

• -    диаграмму предельных амплитуд ст а - ст _т для материала и реальной детали с учетом концентрации напряжений и масштабного фактора;

• -    коэффициент v для различных случаев нагружения;

• -    остаточные напряжения, которые следует принимать в расчетах (максимальные, на поверхности, средние или др.).

В данной работе использована методика построения диаграммы предельных амплитуд цикла напряжений резьбовых деталей с учетом остаточных напряжений, действующих в наиболее нагруженном сечении детали, в которой за основу принята видоизмененная диаграмма Ганна. В осях ст m - ст a строится диаграмма предельных амплитуд цикла для материала резьбового образца (рис. 2). По оси ст a откладывается предел выносливости материала при симметричном цикле в случае растяжения-сжатия ст -1 = ОА, по оси ст m - сопротивление разрыву материала SK = OB. Для ограничения работы материала по текучести по оси абсцисс откладывается предел текучести ст Т = OD и проводится прямая DС под углом 45° к оси абсцисс. Тогда АСD – диаграмма предельных амплитуд цикла напряжений материала резьбового образца, учитывающая как усталость, так и текучесть.

Затем строится диаграмма предельных амплитуд цикла напряжений для резьбовой детали без учета остаточных напряжений во впадинах резьбы.

Во впадине концентратора действует переменное напряжение от внешних сил (рис. 3).

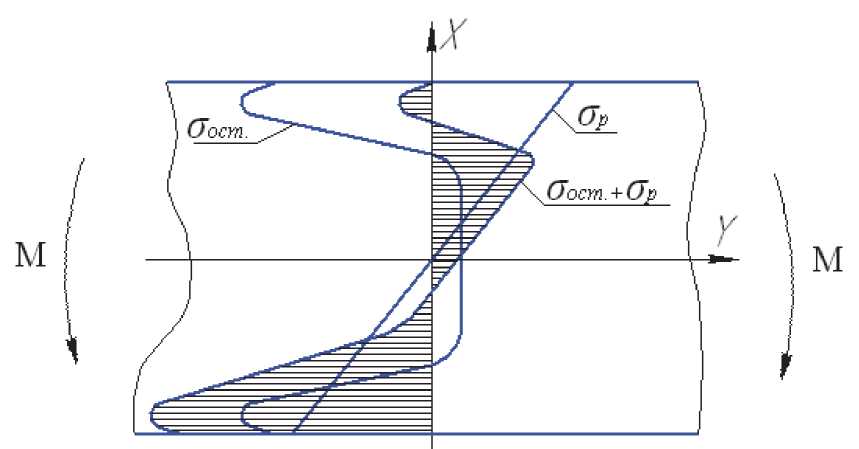
Рис. 1. Сложение остаточных напряжений и рабочих напряжений

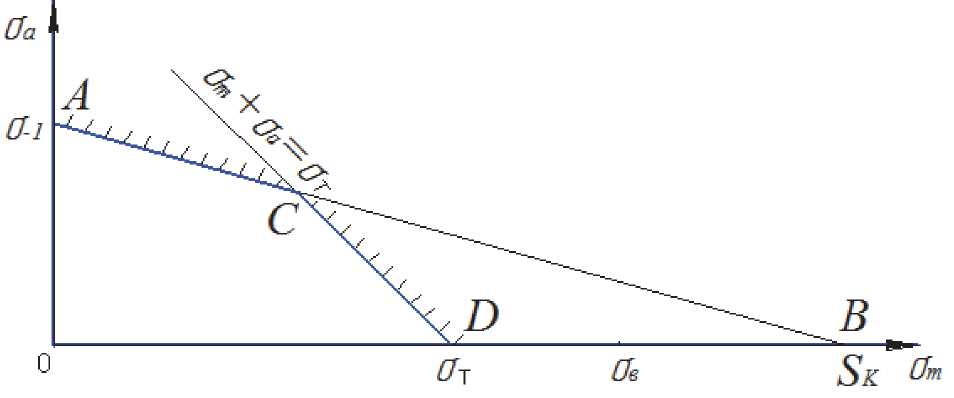
Рис. 2. Диаграмма предельных амплитуд цикла

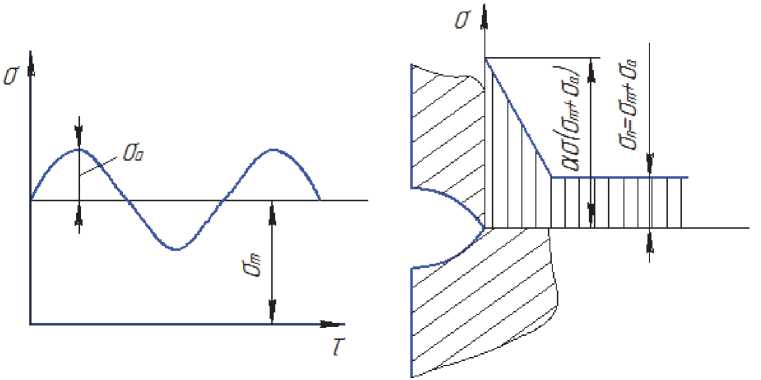
Рис. 3. Напряжения, действующие во впадине концентратора

Наличие концентратора уменьшает предел выносливости материала при симметричном цикле σ _-1 в K _σ раз, где K _σ – эффективный коэффициент концентрации напряжений.

При этом считается, что шероховатость поверхности и размеры поперечного сечения резьбовой детали такие же, как и образца, на котором определяли σ-1 , и эффективный коэффициент концентрации не зависит от асимметрии цикла. По оси ординат откладываются σ-1/Кσ= ОА1, и из точки А проводится прямая А1С1 параллельно АВ до пересечения с прямой D1С1, ограничивающей работу резьбовой детали по текучести. Здесь ОD1 = σТ/ασ, где ασ – теоретический коэффициент концентрации напряжений. Для прямых А1С1 и D1С1 можно записать уравнения через известные механические характеристики материала в виде

σ

^σ a _K

σ

^- - 1

σ

+ -m-K = I, S k ^-

σ a ασ σT

+ ^- m a_- = 1. σ _T

Точка С1 характеризует начало локальной текучести в наиболее нагруженном сечении резьбовой детали, то есть в области впадины резьбы. Решая совместно уравнения, можно определить Т среднее напряжение σт , при котором начинается локальная текучесть:

Т т

σ

ex

S_K ( — - -a ) к Т — 1

К _σ

^a - ⁽ S_K ^{- -} - i )    .

жения А2С2, а для учета действия растягивающих остаточных напряжений – вниз до положения А3С3. Следовательно, для резьбовой детали с сжимающими остаточными напряжениями диаграмма предельных амплитуд цикла будет представлена ломаной А2С2КD, с растягивающими – ломаной А3С3КD.

Для построения диаграммы предельных амплитуд цикла детали с учетом оста-точных напряжений необходимо решить вопрос о том, на какую величину следует переместить прямую A₁C₁. Простой перенос точки С₁ по оси абсцисс на величину максимальных остаточных напряжений неправомерен, так как не учитывает характер распределения остаточных напряжений по толщине поверхностного слоя впадин резьбы и масштабный фактор. Поэтому было предложено перемещать точку A₁ по оси ординат на величину приращения предела выносливости детали с концентратором при симметричном цикле A - - 1 = А 1 А ₂( А 1 А ₃) , используя критерий среднеинтегральных остаточных напряжений σ ост . Таким образом, приращение предела выносливости можно определить по формуле

^{A -} - 1 = У - ^- ост |,

До тех пор, пока напряжения во впадине резьбы не достигнут предела текучести материала σ _Т по всему опасному сечению детали (рис. 4, точка К), предельная амплитуда σ _Rа не будет зависеть от среднего напряжения σ _m, поэтому диаграмма предельных амплитуд цикла резьбовой детали без остаточных напряжений опишется ломаной А₁С₁КD.

Далее строится диаграмма предельных амплитуд цикла напряжений для резьбовой детали с остаточными напряжениями, действующими в ее опасном сечении. Влияние остаточных напряжений на сопротивление усталости детали отождествляется с влиянием средних напряжений цикла. Тогда для учета действия сжимающих остаточных напряжений, увеличивающих предельную амплитуду, левую часть диаграммы следует перемещать параллельно вверх до поло-

где Ψ _σ – коэффициент влияния остаточных напряжений на предел выносливости при симме-

тричном цикле, σ ост - среднеинтегральные остаточные напряжения, определяемые по формуле

σ ост

2 г - z ( в ) ^п 0^ 1 - в²

d β ,

где σ _z ( β ) – осевые остаточные напряжения резьбовой детали в опасном сечении, в = y / 1 КР – относительное расстояние от поверхности впадин резьбы до текущего слоя (рис. 5), выраженное в долях t_кр (t_кр – критическая глубина нераспространяющейся трещины усталости).

Следует отметить, что критерий σ _ост учитывает влияние на предельную амплитуду цикла как характера распределения остаточных напряжений

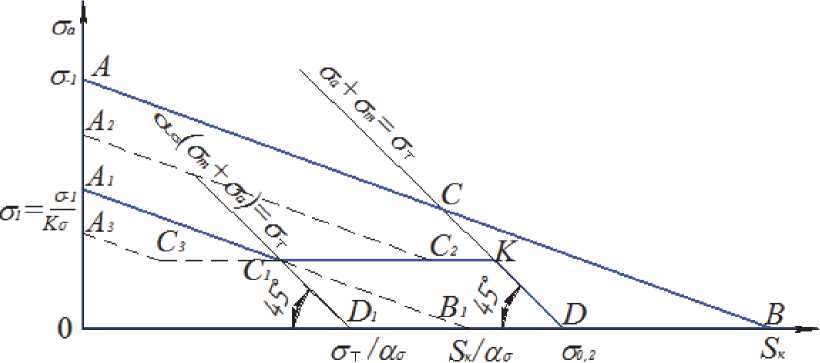
Рис. 4. Диаграмма предельных амплитуд цикла

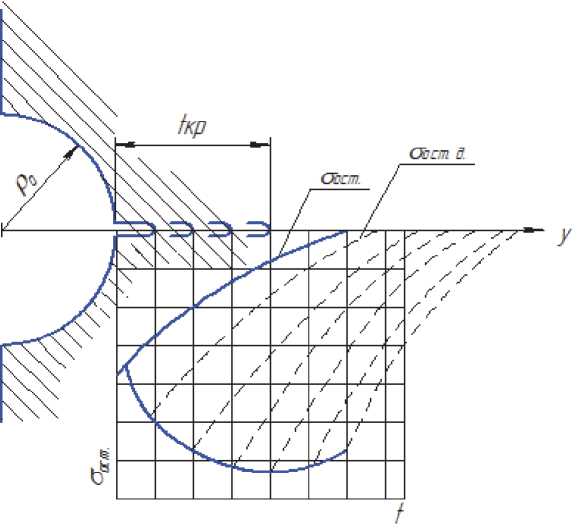
Рис. 5. Распределение остаточных напряжений на дне трещины

в опасном сечении, так и размеров поперечного сечения детали.

Приращение предельной амплитуды ∆ σ _Rа за счет остаточных напряжений во впадинах резьбы в резьбовой детали при любом среднем напряжении σ _т определяется зависимостью:

∆σRa =ψσ(m)σост , где vim) - коэффициент влияния остаточных напряжений на предельную амплитуду при среднем напряжении ат. Коэффициент vim) при ат> Т^ можно вычислить по формуле

• ( т )   — СТ . (<у — О Т)

• -1\ Тщ Тт/

Ψ σ = Ψ σ           _.

^Sк σ ост

При а т ^ а коэффициент v ⁽ m ) необходимо положить равным Ψ_σ , что следует из диаграмм предельных амплитуд цикла напряжений резьбовой детали без остаточных напряжений и с остаточными напряжениями (см. рис. 4).

По результатам исследования остаточных напряжений, полученных при нарезании резьбы с различными по направлению УЗ колебаниями (рис. 6), с помощью методики [1], была проведена оценка усталостных характеристик резьбовых деталей из титанового сплава ВТ16.

По данной методике была получена, представленная на рис. 7, диаграмма предельных амплитуд цикла болтов из сплава ВТ16, изготовленных при наложении различных ультразвуковые колебаний. При этом использовались следующие механиче-

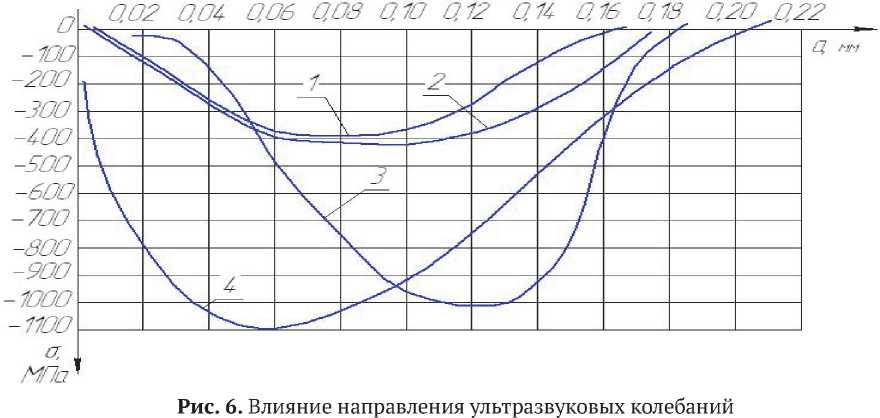
на формирование остаточных напряжений во впадинах резьбы М6x1, ВТ-16: 1 – резание с тангенциальными колебаниями; 2 – обычное резание;

3 – резание с осевыми колебаниями; 4 – резание с радиальными колебаниями

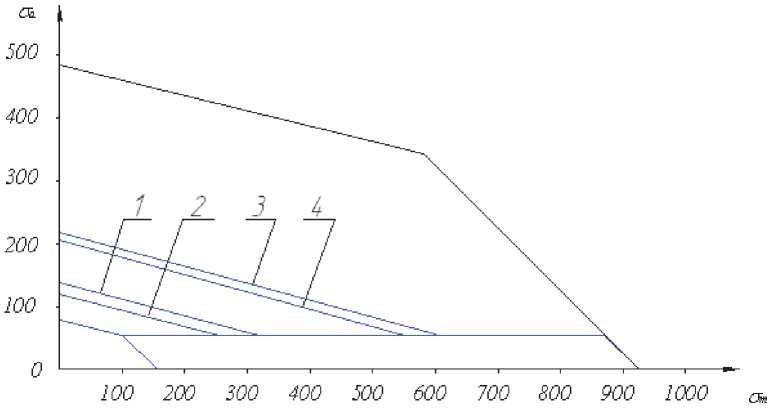
Рис. 7. Диаграмма предельных амплитудцикла болтов из сплава ВТ 16: 1 – обычное резание; 2 – с тангенциальными колебаниями;

3 – с радиальными колебаниями; 4 – с осевыми колебаниями

ские характеристики сплава ВТ 16: σ _B=1180 МПа, σ _0,2 = 920 МПа, δ = 19%, ψ =67%, S _к = 1900 МПа , σ _{- 1} =480 МПа . Для нагруженной резьбы М6 при радиусе впадин ρ =0,17 мм теоретический коэффициент концентрации напряжений α _σ = 6,2, а эффективный коэффициент концентрации K _σ был принят K _σ =6. Следует отметить, что значения α_σ и K _σ близки, и поэтому можно принять K _σ = α _σ , что приведет к расчету в запас прочности с несущественным отклонением. Диаметр опасного сечения детали d = 4,7 мм, что соответствует диаметру впадин резьбы М6,а коэффициент ψ _σ для болтов из сплава ВТ 16 составляет ψ _σ =0,11.

Из представленных данных видно, что при нарезании резьбы на образцах из титанового сплава ВТ16 имеет место увеличение предельной амплитуды цикла в случае обработки с радиальными и осевыми вынужденными ультразвуковыми колебаниями по сравнению с обработкой без использования ультразвука. Введение в зону резания тангенциальных колебаний привело к уменьшению предельной амплитуды цикла. При σ _m = 0 предельная амплитуда цикла σ _а в зависимости от условий обработки распределяется следующим образом:

σ _а = 130 МПа – обычное резание;

σ _а = 100 МПа – резание с тангенциальными колебаниями;

σ _а = 200 МПа – резание с осевыми колебаниями;

σ _а = 220 МПа – резание с радиальными колебаниями.

Из приведённых на рис. 7 данных видно, что при нарезании резьбы с осевыми или радиальными УЗ колебаниями значения предельной амплитуды цикла напряжений в 1,5- 2.2 раза больше, чем при обработке с тангенциальными УЗ колебаниями или без ультразвуковых колебаний.

Таким образом, предел выносливости изменяется прямо пропорционально величине остаточных напряжений, и, следовательно, изменяя технологию изготовления резьбы можно влиять на предел выносливости, который может изменяться в широких пределах, в данном случае от 100 до 220 МПа, т.е. почти в 2 раза.